"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# Plot more images\n",
"torch.manual_seed(42)\n",
"fig = plt.figure(figsize=(9, 9))\n",
"rows, cols = 4, 4\n",
"for i in range(1, rows * cols + 1):\n",
" random_idx = torch.randint(0, len(train_data), size=[1]).item()\n",
" img, label = train_data[random_idx]\n",
" fig.add_subplot(rows, cols, i)\n",
" plt.imshow(img.squeeze(), cmap=\"gray\")\n",
" plt.title(class_names[label])\n",
" plt.axis(False);"
]
},
{
"cell_type": "markdown",
"id": "f356fbe9-95b1-4f81-a82d-dc15b3adc06a",
"metadata": {
"id": "f356fbe9-95b1-4f81-a82d-dc15b3adc06a"
},
"source": [
"Hmmm, this dataset doesn't look too aesthetic.\n",
"\n",
"But the principles we're going to learn on how to build a model for it will be similar across a wide range of computer vision problems.\n",
"\n",
"In essence, taking pixel values and building a model to find patterns in them to use on future pixel values.\n",
"\n",
"Plus, even for this small dataset (yes, even 60,000 images in deep learning is considered quite small), could you write a program to classify each one of them?\n",
"\n",
"You probably could.\n",
"\n",
"But I think coding a model in PyTorch would be faster.\n",
"\n",
"> **Question:** Do you think the above data can be model with only straight (linear) lines? Or do you think you'd also need non-straight (non-linear) lines?"
]
},
{
"cell_type": "markdown",
"id": "43cdd23d-bd1f-4e8c-ba20-22d2b6ac14b1",
"metadata": {
"id": "43cdd23d-bd1f-4e8c-ba20-22d2b6ac14b1"
},
"source": [
"## 2. Prepare DataLoader\n",
"\n",
"Now we've got a dataset ready to go.\n",
"\n",
"The next step is to prepare it with a [`torch.utils.data.DataLoader`](https://pytorch.org/docs/stable/data.html#torch.utils.data.Dataset) or `DataLoader` for short.\n",
"\n",
"The `DataLoader` does what you think it might do.\n",
"\n",
"It helps load data into a model.\n",
"\n",
"For training and for inference.\n",
"\n",
"It turns a large `Dataset` into a Python iterable of smaller chunks.\n",
"\n",
"These smaller chunks are called **batches** or **mini-batches** and can be set by the `batch_size` parameter.\n",
"\n",
"Why do this?\n",
"\n",
"Because it's more computationally efficient.\n",
"\n",
"In an ideal world you could do the forward pass and backward pass across all of your data at once.\n",
"\n",
"But once you start using really large datasets, unless you've got infinite computing power, it's easier to break them up into batches.\n",
"\n",
"It also gives your model more opportunities to improve.\n",
"\n",
"With **mini-batches** (small portions of the data), gradient descent is performed more often per epoch (once per mini-batch rather than once per epoch).\n",
"\n",
"What's a good batch size?\n",
"\n",
"[32 is a good place to start](https://twitter.com/ylecun/status/989610208497360896?s=20&t=N96J_jotN--PYuJk2WcjMw) for a fair amount of problems.\n",
"\n",
"But since this is a value you can set (a **hyperparameter**) you can try all different kinds of values, though generally powers of 2 are used most often (e.g. 32, 64, 128, 256, 512).\n",
"\n",
"\n",
"*Batching FashionMNIST with a batch size of 32 and shuffle turned on. A similar batching process will occur for other datasets but will differ depending on the batch size.*\n",
"\n",
"Let's create `DataLoader`'s for our training and test sets. "
]
},
{
"cell_type": "code",
"execution_count": 10,
"id": "bb2dbf90-a326-43cb-b25b-71af142fafeb",
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/"
},
"id": "bb2dbf90-a326-43cb-b25b-71af142fafeb",
"outputId": "1f563408-3f50-4e8c-a15f-53e2f918b1ac"
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Dataloaders: (, )\n",
"Length of train dataloader: 1875 batches of 32\n",
"Length of test dataloader: 313 batches of 32\n"
]
}
],
"source": [
"from torch.utils.data import DataLoader\n",
"\n",
"# Setup the batch size hyperparameter\n",
"BATCH_SIZE = 32\n",
"\n",
"# Turn datasets into iterables (batches)\n",
"train_dataloader = DataLoader(train_data, # dataset to turn into iterable\n",
" batch_size=BATCH_SIZE, # how many samples per batch? \n",
" shuffle=True # shuffle data every epoch?\n",
")\n",
"\n",
"test_dataloader = DataLoader(test_data,\n",
" batch_size=BATCH_SIZE,\n",
" shuffle=False # don't necessarily have to shuffle the testing data\n",
")\n",
"\n",
"# Let's check out what we've created\n",
"print(f\"Dataloaders: {train_dataloader, test_dataloader}\") \n",
"print(f\"Length of train dataloader: {len(train_dataloader)} batches of {BATCH_SIZE}\")\n",
"print(f\"Length of test dataloader: {len(test_dataloader)} batches of {BATCH_SIZE}\")"
]
},
{
"cell_type": "code",
"execution_count": 11,
"id": "7a925ee7-484b-4149-be8f-3ad790172a5f",
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/"
},
"id": "7a925ee7-484b-4149-be8f-3ad790172a5f",
"outputId": "85815bd7-39e9-44ed-b974-9e30fff5b5ad"
},
"outputs": [
{
"data": {
"text/plain": [
"(torch.Size([32, 1, 28, 28]), torch.Size([32]))"
]
},
"execution_count": 11,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Check out what's inside the training dataloader\n",
"train_features_batch, train_labels_batch = next(iter(train_dataloader))\n",
"train_features_batch.shape, train_labels_batch.shape"
]
},
{
"cell_type": "markdown",
"id": "4fee4cf8-ab73-4c81-8e5e-3c81691e799c",
"metadata": {
"id": "4fee4cf8-ab73-4c81-8e5e-3c81691e799c"
},
"source": [
"And we can see that the data remains unchanged by checking a single sample. "
]
},
{
"cell_type": "code",
"execution_count": 12,
"id": "c863d66a-49be-43be-84dc-372a5d6fc2c2",
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/",
"height": 463
},
"id": "c863d66a-49be-43be-84dc-372a5d6fc2c2",
"outputId": "1052cbcb-6186-4dfe-b5f0-6968bde9fb21"
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Image size: torch.Size([1, 28, 28])\n",
"Label: 6, label size: torch.Size([])\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYUAAAGbCAYAAAAr/4yjAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/bCgiHAAAACXBIWXMAAA9hAAAPYQGoP6dpAAAQuUlEQVR4nO3dX6gfdP3H8fd355ydv9vOGbZl6raT+QcmNmoqXRitGhJUkC5ICCyCCsu7ugh2mxcSQiRIXim7CDFEulCD6A+EyaJCisniKJktmW7u2DnH8z3/PL+L4E1Df+28P23f7Zw9Hpd6Xn6/+/o9PvfV7W1ndXV1NQAgIjZd7CcAwKVDFABIogBAEgUAkigAkEQBgCQKACRRACCJAgBJFLgsdDqd+Pa3v33Or3v00Uej0+nE3/72twv/pOASJAqse3/+85/j0KFDsXv37hgaGoqrrroqDh48GD/60Y8u+GPff//98dRTT13wx4Fe6bh9xHr23HPPxYEDB2LXrl1xzz33xPvf//549dVX4/nnn4+XXnoppqamIuLfnxS+9a1vxUMPPfRf/3orKyuxtLQUg4OD0el0zvn4Y2NjcejQoXj00UfPxw8HLrr+i/0E4H/x/e9/P7Zt2xa///3vY3x8/Kw/9/rrr5f/en19fdHX1/dfv2Z1dTW63W4MDw+X//pwqfOvj1jXXnrppdi7d++7ghARsWPHjnf9saeeeipuuummGBwcjL1798azzz571p9/r/+msGfPnvjsZz8bP//5z2P//v0xPDwcP/7xj6PT6cTc3Fw89thj0el0otPpxFe+8pXz/COE3hIF1rXdu3fHH/7wh/jLX/5yzq/97W9/G/fee2986UtfigceeCC63W7cddddcfr06XNujx8/HnfffXccPHgwfvjDH8a+ffviyJEjMTg4GLfffnscOXIkjhw5Et/4xjfOxw8LLhr/+oh17Tvf+U585jOfiX379sWtt94at99+e3zqU5+KAwcOxMDAwFlf++KLL8axY8fi2muvjYiIAwcOxIc//OH4yU9+cs5fmTQ1NRXPPvts3HHHHWf98W9+85vxwQ9+ML785S+f3x8YXCQ+KbCuHTx4MH73u9/F5z//+XjhhRfigQceiDvuuCOuuuqq+NnPfnbW137605/OIERE3HzzzbF169Z4+eWXz/k4k5OT7woCbESiwLp3yy23xJNPPhlnzpyJo0ePxve+972YmZmJQ4cOxbFjx/Lrdu3a9a7txMREnDlz5pyPMTk5eV6fM1yqRIENY/PmzXHLLbfE/fffHw8//HAsLS3FE088kX/+//tVRWv5Vdl+pRGXC1FgQ9q/f39ERLz22msX9HHW8nsZYD0RBda1X/3qV+/5M/2nn346IiJuuOGGC/r4o6OjMT09fUEfA3rJrz5iXbvvvvvi7bffji984Qtx4403xuLiYjz33HPx+OOPx549e+KrX/3qBX38j370o/GLX/wiHnzwwfjABz4Qk5OTcdttt13Qx4QLSRRY137wgx/EE088EU8//XQ88sgjsbi4GLt27Yp77703Dh8+/J6/qe18evDBB+PrX/96HD58OObn5+Oee+4RBdY1t48ASP6bAgBJFABIogBAEgUAkigAkEQBgLTm36fgt/Nzsezevbu8+fjHP17e/PGPfyxv3ve+95U3v/71r8ubVi3ft36V+sa1lr+3PikAkEQBgCQKACRRACCJAgBJFABIogBAEgUAkigAkEQBgCQKACRRACCt+f/R7CBeb7W+3hvxmNnDDz9c3uzdu7e8+elPf1re3HnnneXNQw89VN5EtD2/jciRv3YO4gFQIgoAJFEAIIkCAEkUAEiiAEASBQCSKACQRAGAJAoAJFEAIIkCAKn/Yj8B3tulfsBr586d5c0nP/nJpsc6depUeTMyMlLefPe73y1vpqeny5uPfexj5U1ExOnTp8ub48ePlzf//Oc/y5teutS/N9Y7nxQASKIAQBIFAJIoAJBEAYAkCgAkUQAgiQIASRQASKIAQBIFAJIoAJBEAYDUWV3jycFOp3Ohnwv/4aabbmra7du3r7z50Ic+1PRYVZOTk027LVu2lDfXXXddedPymrdccH3++efLm4iIbdu2lTfPPPNMedPtdsubf/zjH+XN0aNHy5uIiFdeeaVpx9ouzPqkAEASBQCSKACQRAGAJAoAJFEAIIkCAEkUAEiiAEASBQCSKACQRAGA5CBeD9x8883lzRe/+MWmxzp27Fh5s7y8XN688cYb5c3+/fvLm4iIO++8s7x57LHHypuvfe1r5U3Lcbarr766vImI+Pvf/17ePPLII+XN+Ph4eXPFFVeUN9u3by9vItp+TKdPn256rI3GQTwASkQBgCQKACRRACCJAgBJFABIogBAEgUAkigAkEQBgCQKACRRACA5iNcD9913X3nz5ptvNj1Wy4G2sbGx8qa/v7+8ef3118ubiIjZ2dnyZuvWreXN3XffXd6cOHGivPnNb35T3kRErKyslDc7d+4sb7rdbnnT8s+HK6+8sryJiFhcXCxvHn/88abH2mgcxAOgRBQASKIAQBIFAJIoAJBEAYAkCgAkUQAgiQIASRQASKIAQBIFAFL9qhlle/bsKW/OnDnT9FgTExNNu17YsWNH027Lli3lzTvvvFPeLC8vlzcvvvhieTMwMFDeRETs2rWrvGk5bjc0NFTetBzr27Sp7eek119/fdOOtfFJAYAkCgAkUQAgiQIASRQASKIAQBIFAJIoAJBEAYAkCgAkUQAgiQIAyUG8ohtvvLG8WV1dLW+2bdtW3kS0HUBrOQQ3Pz9f3nQ6nfImou3Y2vDwcHnTcoTw5MmT5U3Lgb+Itte8v7/+Ld7yfmh5v27durW8iYhYWFgob2644Yby5vjx4+XNRuCTAgBJFABIogBAEgUAkigAkEQBgCQKACRRACCJAgBJFABIogBAEgUAkigAkFxJLfrEJz5R3rRcW9y8eXN5ExExMTFR3szOzpY309PT5U1fX195ExGxtLRU3oyOjpY3r732WnmzaVPvfl41NzdX3uzYsaO8GRwcLG927txZ3pw4caK8iWh7j3/kIx8pb1xJBeCyJwoAJFEAIIkCAEkUAEiiAEASBQCSKACQRAGAJAoAJFEAIIkCAMlBvKLrrruuvPnTn/5U3kxNTZU3ERG33XZbeTM+Pl7e9PfX3zqnTp0qbyLajgMODAyUN2+++WZ50/LcxsbGypuIiIWFhfJm69at5U3L+6HlQOIrr7xS3kREXH/99eVNy5G/y5VPCgAkUQAgiQIASRQASKIAQBIFAJIoAJBEAYAkCgAkUQAgiQIASRQASJf1QbyWw1qzs7PlTV9fX3mzsrJS3kREdDqd8mZ5ebm8mZiYKG8WFxfLm4iIbrdb3rQcnWt5zbdt21betBypi2g76tZysK/lcVr+3o6MjJQ3ERFvvPFGedPy9/aaa64pb1599dXy5lLjkwIASRQASKIAQBIFAJIoAJBEAYAkCgAkUQAgiQIASRQASKIAQBIFANJlfRDvyiuvLG9ajrO1HNZqPR539dVXlzdTU1PlzdzcXHnTquU1bzkE12JhYaG8aTmqGNH2OuzcubO8aTke13KAcGBgoLxp1fI67Nu3r7xxEA+ADUUUAEiiAEASBQCSKACQRAGAJAoAJFEAIIkCAEkUAEiiAEASBQCSKACQOqurq6tr+sJO50I/lw1r9+7d5c2WLVuaHutzn/tceTM4OFjenDhxoryZn58vbyIiZmZmypuWK6lr/FY4S6+u5ka0XRV95513ypvt27eXN9dee21588wzz5Q3EREnT54sb44dO9aTx7nUreU97pMCAEkUAEiiAEASBQCSKACQRAGAJAoAJFEAIIkCAEkUAEiiAEASBQCSg3gbzMTERHlz+PDh8uavf/1refP222+XNxFtR91ajsetrKyUNy3PrWUTETE2NtaTTctr9+STT5Y3U1NT5Q3/GwfxACgRBQCSKACQRAGAJAoAJFEAIIkCAEkUAEiiAEASBQCSKACQRAGA1H+xn8DF1HLkr1eHAVuPpnW73fJmjTcRz9LfX3/rtGwiIhYXF8ublqNuLcfjTp48Wd4MDQ2VNxERy8vL5U3La9fyOJf6cbuW79uW74uNwCcFAJIoAJBEAYAkCgAkUQAgiQIASRQASKIAQBIFAJIoAJBEAYAkCgCky/ogXouWQ3W9OqIXETE/P9+TTcvBuVYtB9pafkwtB9AGBwd78jgREZs3by5vRkdHy5uZmZny5lJ3uR63a+GTAgBJFABIogBAEgUAkigAkEQBgCQKACRRACCJAgBJFABIogBAEgUA0mV9EK9XR7Iu9WNcCwsL5U1/f/2t09fXV95ERAwPD5c3Q0ND5U3L4cKWTctRxVYjIyPlzenTpy/AM2G98EkBgCQKACRRACCJAgBJFABIogBAEgUAkigAkEQBgCQKACRRACCJAgBJFABIl/WVVP5teXm5vGm5XDo7O1veRLRdcW25XtpyWfVf//pXebNpU9vPxXp1xXV6erq8YePwSQGAJAoAJFEAIIkCAEkUAEiiAEASBQCSKACQRAGAJAoAJFEAIIkCAMlBPJqOpvX31986fX195U1E26G6FktLS+VNy3Nreb0j2l7zlsOFLQcS2Th8UgAgiQIASRQASKIAQBIFAJIoAJBEAYAkCgAkUQAgiQIASRQASKIAQHIQj1hZWSlvNm2q/3yi9RBcy2ONjo6WNy3H7ebm5sqbxcXF8qZVyxHClvcDG4dPCgAkUQAgiQIASRQASKIAQBIFAJIoAJBEAYAkCgAkUQAgiQIASRQASA7iEUtLS+XNyMhIedPf3/Z263a75c3AwEB5s7y8XN5MT0+XN+Pj4+VNRNtxu9bXnMuXTwoAJFEAIIkCAEkUAEiiAEASBQCSKACQRAGAJAoAJFEAIIkCAEkUAEiuZdGk0+n0ZBPRdgjuzJkz5c0VV1xR3rQet+uVoaGhnmzYOHxSACCJAgBJFABIogBAEgUAkigAkEQBgCQKACRRACCJAgBJFABIogBAEgUAkiupxNLSUnnT319/6ywvL5c3EREDAwM92QwPD5c3c3Nz5U232y1vIiIGBwebdlUtrx0bh08KACRRACCJAgBJFABIogBAEgUAkigAkEQBgCQKACRRACCJAgBJFABIDuIR8/Pz5U3L8bi+vr7yJiJidna2vOl0Oj15nJmZmfJmZGSkvImIWFlZ6cmm9XAhG4NPCgAkUQAgiQIASRQASKIAQBIFAJIoAJBEAYAkCgAkUQAgiQIASRQASA7i0XQ8bvPmzT3ZRLQd3xsfHy9vhoaGyptut9uTx2nV8linTp26AM/k3VredxERq6ur5/mZ8J98UgAgiQIASRQASKIAQBIFAJIoAJBEAYAkCgAkUQAgiQIASRQASKIAQHIQj6ajaQsLC+XNli1bypuIiL6+vvLmrbfeKm9anl8vj9u1GBsbK29aXjs2Dp8UAEiiAEASBQCSKACQRAGAJAoAJFEAIIkCAEkUAEiiAEASBQCSKACQRAGA5ErqJarT6TTtVldXy5uZmZny5tZbby1vfvnLX5Y3EREDAwPlTct10NHR0fKm2+2WNy2vd0TE8PBweTM+Pl7eTE9PlzdsHD4pAJBEAYAkCgAkUQAgiQIASRQASKIAQBIFAJIoAJBEAYAkCgAkUQAgdVbXeEGt9UAbG9PevXvLm6WlpabHuuaaa8qbycnJ8mb79u3lzcmTJ8ub1u+lt956q7w5ceJEeXP06NHyhvVhLf+490kBgCQKACRRACCJAgBJFABIogBAEgUAkigAkEQBgCQKACRRACCJAgCpf61fuMa7eQCsYz4pAJBEAYAkCgAkUQAgiQIASRQASKIAQBIFAJIoAJD+DweYWJOnM3TKAAAAAElFTkSuQmCC\n",
"text/plain": [
"
"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# Show a sample\n",
"torch.manual_seed(42)\n",
"random_idx = torch.randint(0, len(train_features_batch), size=[1]).item()\n",
"img, label = train_features_batch[random_idx], train_labels_batch[random_idx]\n",
"plt.imshow(img.squeeze(), cmap=\"gray\")\n",
"plt.title(class_names[label])\n",
"plt.axis(\"Off\");\n",
"print(f\"Image size: {img.shape}\")\n",
"print(f\"Label: {label}, label size: {label.shape}\")"
]
},
{
"cell_type": "markdown",
"id": "db1695cf-f53d-4c7c-ad39-dfed76533125",
"metadata": {
"id": "db1695cf-f53d-4c7c-ad39-dfed76533125"
},
"source": [
"## 3. Model 0: Build a baseline model\n",
"\n",
"Data loaded and prepared!\n",
"\n",
"Time to build a **baseline model** by subclassing `nn.Module`.\n",
"\n",
"A **baseline model** is one of the simplest models you can imagine.\n",
"\n",
"You use the baseline as a starting point and try to improve upon it with subsequent, more complicated models.\n",
"\n",
"Our baseline will consist of two [`nn.Linear()`](https://pytorch.org/docs/stable/generated/torch.nn.Linear.html) layers.\n",
"\n",
"We've done this in a previous section but there's going to one slight difference.\n",
"\n",
"Because we're working with image data, we're going to use a different layer to start things off.\n",
"\n",
"And that's the [`nn.Flatten()`](https://pytorch.org/docs/stable/generated/torch.nn.Flatten.html) layer.\n",
"\n",
"`nn.Flatten()` compresses the dimensions of a tensor into a single vector.\n",
"\n",
"This is easier to understand when you see it."
]
},
{
"cell_type": "code",
"execution_count": 13,
"id": "405319f1-f242-4bd9-90f5-3abdc50782ac",
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/"
},
"id": "405319f1-f242-4bd9-90f5-3abdc50782ac",
"outputId": "742cd0fe-c95f-4201-a469-f12733625784"
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Shape before flattening: torch.Size([1, 28, 28]) -> [color_channels, height, width]\n",
"Shape after flattening: torch.Size([1, 784]) -> [color_channels, height*width]\n"
]
}
],
"source": [
"# Create a flatten layer\n",
"flatten_model = nn.Flatten() # all nn modules function as a model (can do a forward pass)\n",
"\n",
"# Get a single sample\n",
"x = train_features_batch[0]\n",
"\n",
"# Flatten the sample\n",
"output = flatten_model(x) # perform forward pass\n",
"\n",
"# Print out what happened\n",
"print(f\"Shape before flattening: {x.shape} -> [color_channels, height, width]\")\n",
"print(f\"Shape after flattening: {output.shape} -> [color_channels, height*width]\")\n",
"\n",
"# Try uncommenting below and see what happens\n",
"#print(x)\n",
"#print(output)"
]
},
{
"cell_type": "markdown",
"id": "86bb7806-fca6-45af-8111-3e00e38f5be9",
"metadata": {
"id": "86bb7806-fca6-45af-8111-3e00e38f5be9"
},
"source": [
"The `nn.Flatten()` layer took our shape from `[color_channels, height, width]` to `[color_channels, height*width]`.\n",
"\n",
"Why do this?\n",
"\n",
"Because we've now turned our pixel data from height and width dimensions into one long **feature vector**.\n",
"\n",
"And `nn.Linear()` layers like their inputs to be in the form of feature vectors.\n",
"\n",
"Let's create our first model using `nn.Flatten()` as the first layer. "
]
},
{
"cell_type": "code",
"execution_count": 14,
"id": "1449f427-6859-41ae-8133-50b58ffbce72",
"metadata": {
"id": "1449f427-6859-41ae-8133-50b58ffbce72"
},
"outputs": [],
"source": [
"from torch import nn\n",
"class FashionMNISTModelV0(nn.Module):\n",
" def __init__(self, input_shape: int, hidden_units: int, output_shape: int):\n",
" super().__init__()\n",
" self.layer_stack = nn.Sequential(\n",
" nn.Flatten(), # neural networks like their inputs in vector form\n",
" nn.Linear(in_features=input_shape, out_features=hidden_units), # in_features = number of features in a data sample (784 pixels)\n",
" nn.Linear(in_features=hidden_units, out_features=output_shape)\n",
" )\n",
" \n",
" def forward(self, x):\n",
" return self.layer_stack(x)"
]
},
{
"cell_type": "markdown",
"id": "4d1b50bf-d00b-485c-be00-b3e4de156fab",
"metadata": {
"id": "4d1b50bf-d00b-485c-be00-b3e4de156fab"
},
"source": [
"Wonderful!\n",
"\n",
"We've got a baseline model class we can use, now let's instantiate a model.\n",
"\n",
"We'll need to set the following parameters:\n",
"* `input_shape=784` - this is how many features you've got going in the model, in our case, it's one for every pixel in the target image (28 pixels high by 28 pixels wide = 784 features).\n",
"* `hidden_units=10` - number of units/neurons in the hidden layer(s), this number could be whatever you want but to keep the model small we'll start with `10`.\n",
"* `output_shape=len(class_names)` - since we're working with a multi-class classification problem, we need an output neuron per class in our dataset.\n",
"\n",
"Let's create an instance of our model and send to the CPU for now (we'll run a small test for running `model_0` on CPU vs. a similar model on GPU soon)."
]
},
{
"cell_type": "code",
"execution_count": 15,
"id": "dd18384a-76f9-4b5a-a013-fda077f16865",
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/"
},
"id": "dd18384a-76f9-4b5a-a013-fda077f16865",
"outputId": "e4b63839-d012-40db-a7f7-967a146fe566"
},
"outputs": [
{
"data": {
"text/plain": [
"FashionMNISTModelV0(\n",
" (layer_stack): Sequential(\n",
" (0): Flatten(start_dim=1, end_dim=-1)\n",
" (1): Linear(in_features=784, out_features=10, bias=True)\n",
" (2): Linear(in_features=10, out_features=10, bias=True)\n",
" )\n",
")"
]
},
"execution_count": 15,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"torch.manual_seed(42)\n",
"\n",
"# Need to setup model with input parameters\n",
"model_0 = FashionMNISTModelV0(input_shape=784, # one for every pixel (28x28)\n",
" hidden_units=10, # how many units in the hiden layer\n",
" output_shape=len(class_names) # one for every class\n",
")\n",
"model_0.to(\"cpu\") # keep model on CPU to begin with "
]
},
{
"cell_type": "markdown",
"id": "03243179-1cdc-45d9-8b8c-82538ac02e9c",
"metadata": {
"id": "03243179-1cdc-45d9-8b8c-82538ac02e9c"
},
"source": [
"### 3.1 Setup loss, optimizer and evaluation metrics\n",
"\n",
"Since we're working on a classification problem, let's bring in our [`helper_functions.py` script](https://github.com/mrdbourke/pytorch-deep-learning/blob/main/helper_functions.py) and subsequently the `accuracy_fn()` we defined in [notebook 02](https://www.learnpytorch.io/02_pytorch_classification/).\n",
"\n",
"> **Note:** Rather than importing and using our own accuracy function or evaluation metric(s), you could import various evaluation metrics from the [TorchMetrics package](https://torchmetrics.readthedocs.io/en/latest/)."
]
},
{
"cell_type": "code",
"execution_count": 16,
"id": "31c91f17-d810-46a4-97c3-c734f93430b1",
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/"
},
"id": "31c91f17-d810-46a4-97c3-c734f93430b1",
"outputId": "d2333811-f5fa-426f-90a7-c884fe2493df"
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Downloading helper_functions.py\n"
]
}
],
"source": [
"import requests\n",
"from pathlib import Path \n",
"\n",
"# Download helper functions from Learn PyTorch repo (if not already downloaded)\n",
"if Path(\"helper_functions.py\").is_file():\n",
" print(\"helper_functions.py already exists, skipping download\")\n",
"else:\n",
" print(\"Downloading helper_functions.py\")\n",
" # Note: you need the \"raw\" GitHub URL for this to work\n",
" request = requests.get(\"https://raw.githubusercontent.com/mrdbourke/pytorch-deep-learning/main/helper_functions.py\")\n",
" with open(\"helper_functions.py\", \"wb\") as f:\n",
" f.write(request.content)"
]
},
{
"cell_type": "code",
"execution_count": 17,
"id": "ce3d13b8-f018-4b44-8bba-375074dc4c5f",
"metadata": {
"id": "ce3d13b8-f018-4b44-8bba-375074dc4c5f"
},
"outputs": [],
"source": [
"# Import accuracy metric\n",
"from helper_functions import accuracy_fn # Note: could also use torchmetrics.Accuracy(task = 'multiclass', num_classes=len(class_names)).to(device)\n",
"\n",
"# Setup loss function and optimizer\n",
"loss_fn = nn.CrossEntropyLoss() # this is also called \"criterion\"/\"cost function\" in some places\n",
"optimizer = torch.optim.SGD(params=model_0.parameters(), lr=0.1)"
]
},
{
"cell_type": "markdown",
"id": "4109f867-83f2-4394-a925-8acdc63ccffe",
"metadata": {
"id": "4109f867-83f2-4394-a925-8acdc63ccffe"
},
"source": [
"### 3.2 Creating a function to time our experiments\n",
"\n",
"Loss function and optimizer ready!\n",
"\n",
"It's time to start training a model.\n",
"\n",
"But how about we do a little experiment while we train.\n",
"\n",
"I mean, let's make a timing function to measure the time it takes our model to train on CPU versus using a GPU.\n",
"\n",
"We'll train this model on the CPU but the next one on the GPU and see what happens.\n",
"\n",
"Our timing function will import the [`timeit.default_timer()` function](https://docs.python.org/3/library/timeit.html#timeit.default_timer) from the Python [`timeit` module](https://docs.python.org/3/library/timeit.html)."
]
},
{
"cell_type": "code",
"execution_count": 18,
"id": "31adc3fe-ce90-4b4e-b0d4-3613abae5714",
"metadata": {
"id": "31adc3fe-ce90-4b4e-b0d4-3613abae5714"
},
"outputs": [],
"source": [
"from timeit import default_timer as timer \n",
"def print_train_time(start: float, end: float, device: torch.device = None):\n",
" \"\"\"Prints difference between start and end time.\n",
"\n",
" Args:\n",
" start (float): Start time of computation (preferred in timeit format). \n",
" end (float): End time of computation.\n",
" device ([type], optional): Device that compute is running on. Defaults to None.\n",
"\n",
" Returns:\n",
" float: time between start and end in seconds (higher is longer).\n",
" \"\"\"\n",
" total_time = end - start\n",
" print(f\"Train time on {device}: {total_time:.3f} seconds\")\n",
" return total_time"
]
},
{
"cell_type": "markdown",
"id": "07b9560e-f5dc-45d6-b3b2-ddae17a71b34",
"metadata": {
"id": "07b9560e-f5dc-45d6-b3b2-ddae17a71b34"
},
"source": [
"### 3.3 Creating a training loop and training a model on batches of data\n",
"\n",
"Beautiful!\n",
"\n",
"Looks like we've got all of the pieces of the puzzle ready to go, a timer, a loss function, an optimizer, a model and most importantly, some data.\n",
"\n",
"Let's now create a training loop and a testing loop to train and evaluate our model.\n",
"\n",
"We'll be using the same steps as the previous notebook(s), though since our data is now in batch form, we'll add another loop to loop through our data batches.\n",
"\n",
"Our data batches are contained within our `DataLoader`s, `train_dataloader` and `test_dataloader` for the training and test data splits respectively.\n",
"\n",
"A batch is `BATCH_SIZE` samples of `X` (features) and `y` (labels), since we're using `BATCH_SIZE=32`, our batches have 32 samples of images and targets.\n",
"\n",
"And since we're computing on batches of data, our loss and evaluation metrics will be calculated **per batch** rather than across the whole dataset.\n",
"\n",
"This means we'll have to divide our loss and accuracy values by the number of batches in each dataset's respective dataloader. \n",
"\n",
"Let's step through it: \n",
"1. Loop through epochs.\n",
"2. Loop through training batches, perform training steps, calculate the train loss *per batch*.\n",
"3. Loop through testing batches, perform testing steps, calculate the test loss *per batch*.\n",
"4. Print out what's happening.\n",
"5. Time it all (for fun).\n",
"\n",
"A fair few steps but...\n",
"\n",
"...if in doubt, code it out. "
]
},
{
"cell_type": "code",
"execution_count": 19,
"id": "c07bbf10-81e3-47f0-990d-9a4a838276ab",
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/",
"height": 587,
"referenced_widgets": [
"0bd8f8b5ff4d4b50b03e3a65cc1446f0",
"430d171cfd584196ad0fa3e1cd0a286c",
"618fb3cf63a94da9ad5f29a3d9a87ac3",
"3524e24faad44aa38926b40b2d590f6b",
"c01ca4def9224135ad367b6f8dbbae62",
"decc1966e6a84973839efc0c65f51790",
"39fc424b6cef4e98a80a342f530be99b",
"e929063168354b018bbf0bb45fdfef1f",
"d62646457b284fcb8aeac382b77eb942",
"5c0883aa74f94568850741dad118cb88",
"e44697d8dd41492e8619a860b3911e19"
]
},
"id": "c07bbf10-81e3-47f0-990d-9a4a838276ab",
"outputId": "3fb70da8-1a65-42bb-a684-85f0d1dd11c0"
},
"outputs": [
{
"data": {
"application/vnd.jupyter.widget-view+json": {
"model_id": "0bd8f8b5ff4d4b50b03e3a65cc1446f0",
"version_major": 2,
"version_minor": 0
},
"text/plain": [
" 0%| | 0/3 [00:00 pred_prob -> pred_labels)\n",
" \n",
" # Scale loss and acc to find the average loss/acc per batch\n",
" loss /= len(data_loader)\n",
" acc /= len(data_loader)\n",
" \n",
" return {\"model_name\": model.__class__.__name__, # only works when model was created with a class\n",
" \"model_loss\": loss.item(),\n",
" \"model_acc\": acc}\n",
"\n",
"# Calculate model 0 results on test dataset\n",
"model_0_results = eval_model(model=model_0, data_loader=test_dataloader,\n",
" loss_fn=loss_fn, accuracy_fn=accuracy_fn\n",
")\n",
"model_0_results"
]
},
{
"cell_type": "markdown",
"id": "a39c3042-1262-4d1f-b33e-c8e2ba6781d3",
"metadata": {
"id": "a39c3042-1262-4d1f-b33e-c8e2ba6781d3"
},
"source": [
"Looking good!\n",
"\n",
"We can use this dictionary to compare the baseline model results to other models later on."
]
},
{
"cell_type": "markdown",
"id": "3b76784d-4cdb-43d2-a6da-8e4da9a812a9",
"metadata": {
"id": "3b76784d-4cdb-43d2-a6da-8e4da9a812a9"
},
"source": [
"## 5. Setup device agnostic-code (for using a GPU if there is one)\n",
"We've seen how long it takes to train ma PyTorch model on 60,000 samples on CPU.\n",
"\n",
"> **Note:** Model training time is dependent on hardware used. Generally, more processors means faster training and smaller models on smaller datasets will often train faster than large models and large datasets.\n",
"\n",
"Now let's setup some [device-agnostic code](https://pytorch.org/docs/stable/notes/cuda.html#best-practices) for our models and data to run on GPU if it's available.\n",
"\n",
"If you're running this notebook on Google Colab, and you don't a GPU turned on yet, it's now time to turn one on via `Runtime -> Change runtime type -> Hardware accelerator -> GPU`. If you do this, your runtime will likely reset and you'll have to run all of the cells above by going `Runtime -> Run before`."
]
},
{
"cell_type": "code",
"execution_count": 21,
"id": "17b69fe9-f974-4538-922c-20c5cc8220cc",
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/",
"height": 35
},
"id": "17b69fe9-f974-4538-922c-20c5cc8220cc",
"outputId": "10c3b74b-4db7-4a30-8c3a-5a259d1f54b8"
},
"outputs": [
{
"data": {
"application/vnd.google.colaboratory.intrinsic+json": {
"type": "string"
},
"text/plain": [
"'cuda'"
]
},
"execution_count": 21,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Setup device agnostic code\n",
"import torch\n",
"device = \"cuda\" if torch.cuda.is_available() else \"cpu\"\n",
"device"
]
},
{
"cell_type": "markdown",
"id": "514021a8-d6f2-47f3-ab50-55f844e42310",
"metadata": {
"id": "514021a8-d6f2-47f3-ab50-55f844e42310"
},
"source": [
"Beautiful!\n",
"\n",
"Let's build another model."
]
},
{
"cell_type": "markdown",
"id": "d7893907-5f82-4c5e-8fde-fa542a9f25af",
"metadata": {
"id": "d7893907-5f82-4c5e-8fde-fa542a9f25af"
},
"source": [
"## 6. Model 1: Building a better model with non-linearity\n",
"\n",
"We learned about [the power of non-linearity in notebook 02](https://www.learnpytorch.io/02_pytorch_classification/#6-the-missing-piece-non-linearity).\n",
"\n",
"Seeing the data we've been working with, do you think it needs non-linear functions?\n",
"\n",
"And remember, linear means straight and non-linear means non-straight.\n",
"\n",
"Let's find out.\n",
"\n",
"We'll do so by recreating a similar model to before, except this time we'll put non-linear functions (`nn.ReLU()`) in between each linear layer."
]
},
{
"cell_type": "code",
"execution_count": 22,
"id": "2ccce5f2-b1e5-47a6-a7f3-6bc096b35ffb",
"metadata": {
"id": "2ccce5f2-b1e5-47a6-a7f3-6bc096b35ffb"
},
"outputs": [],
"source": [
"# Create a model with non-linear and linear layers\n",
"class FashionMNISTModelV1(nn.Module):\n",
" def __init__(self, input_shape: int, hidden_units: int, output_shape: int):\n",
" super().__init__()\n",
" self.layer_stack = nn.Sequential(\n",
" nn.Flatten(), # flatten inputs into single vector\n",
" nn.Linear(in_features=input_shape, out_features=hidden_units),\n",
" nn.ReLU(),\n",
" nn.Linear(in_features=hidden_units, out_features=output_shape),\n",
" nn.ReLU()\n",
" )\n",
" \n",
" def forward(self, x: torch.Tensor):\n",
" return self.layer_stack(x)"
]
},
{
"cell_type": "markdown",
"id": "4b4b7a2f-4834-4aa1-a8e2-b6e3e2b49224",
"metadata": {
"id": "4b4b7a2f-4834-4aa1-a8e2-b6e3e2b49224"
},
"source": [
"That looks good.\n",
"\n",
"Now let's instantiate it with the same settings we used before.\n",
"\n",
"We'll need `input_shape=784` (equal to the number of features of our image data), `hidden_units=10` (starting small and the same as our baseline model) and `output_shape=len(class_names)` (one output unit per class).\n",
"\n",
"> **Note:** Notice how we kept most of the settings of our model the same except for one change: adding non-linear layers. This is a standard practice for running a series of machine learning experiments, change one thing and see what happens, then do it again, again, again."
]
},
{
"cell_type": "code",
"execution_count": 23,
"id": "907091ec-7e46-470b-a305-788a3009b837",
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/"
},
"id": "907091ec-7e46-470b-a305-788a3009b837",
"outputId": "4cecd2df-2918-4368-fa33-7aea8f958d8f"
},
"outputs": [
{
"data": {
"text/plain": [
"device(type='cuda', index=0)"
]
},
"execution_count": 23,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"torch.manual_seed(42)\n",
"model_1 = FashionMNISTModelV1(input_shape=784, # number of input features\n",
" hidden_units=10,\n",
" output_shape=len(class_names) # number of output classes desired\n",
").to(device) # send model to GPU if it's available\n",
"next(model_1.parameters()).device # check model device"
]
},
{
"cell_type": "markdown",
"id": "b54a4e9d-a7ad-404c-920f-485fcff18a92",
"metadata": {
"id": "b54a4e9d-a7ad-404c-920f-485fcff18a92"
},
"source": [
"### 6.1 Setup loss, optimizer and evaluation metrics\n",
"\n",
"As usual, we'll setup a loss function, an optimizer and an evaluation metric (we could do multiple evaluation metrics but we'll stick with accuracy for now)."
]
},
{
"cell_type": "code",
"execution_count": 24,
"id": "fe7e463b-d46c-4f00-853c-fdf0a28d74c8",
"metadata": {
"id": "fe7e463b-d46c-4f00-853c-fdf0a28d74c8"
},
"outputs": [],
"source": [
"from helper_functions import accuracy_fn\n",
"loss_fn = nn.CrossEntropyLoss()\n",
"optimizer = torch.optim.SGD(params=model_1.parameters(), \n",
" lr=0.1)"
]
},
{
"cell_type": "markdown",
"id": "1eb30af6-a355-49a2-a59f-25169fd27a6e",
"metadata": {
"id": "1eb30af6-a355-49a2-a59f-25169fd27a6e"
},
"source": [
"### 6.2 Functionizing training and test loops\n",
"\n",
"So far we've been writing train and test loops over and over. \n",
"\n",
"Let's write them again but this time we'll put them in functions so they can be called again and again.\n",
"\n",
"And because we're using device-agnostic code now, we'll be sure to call `.to(device)` on our feature (`X`) and target (`y`) tensors.\n",
"\n",
"For the training loop we'll create a function called `train_step()` which takes in a model, a `DataLoader` a loss function and an optimizer.\n",
"\n",
"The testing loop will be similar but it'll be called `test_step()` and it'll take in a model, a `DataLoader`, a loss function and an evaluation function.\n",
"\n",
"> **Note:** Since these are functions, you can customize them in any way you like. What we're making here can be considered barebones training and testing functions for our specific classification use case."
]
},
{
"cell_type": "code",
"execution_count": 25,
"id": "3d239ed2-4028-4603-8db3-ffca2b727819",
"metadata": {
"id": "3d239ed2-4028-4603-8db3-ffca2b727819"
},
"outputs": [],
"source": [
"def train_step(model: torch.nn.Module,\n",
" data_loader: torch.utils.data.DataLoader,\n",
" loss_fn: torch.nn.Module,\n",
" optimizer: torch.optim.Optimizer,\n",
" accuracy_fn,\n",
" device: torch.device = device):\n",
" train_loss, train_acc = 0, 0\n",
" model.to(device)\n",
" for batch, (X, y) in enumerate(data_loader):\n",
" # Send data to GPU\n",
" X, y = X.to(device), y.to(device)\n",
"\n",
" # 1. Forward pass\n",
" y_pred = model(X)\n",
"\n",
" # 2. Calculate loss\n",
" loss = loss_fn(y_pred, y)\n",
" train_loss += loss\n",
" train_acc += accuracy_fn(y_true=y,\n",
" y_pred=y_pred.argmax(dim=1)) # Go from logits -> pred labels\n",
"\n",
" # 3. Optimizer zero grad\n",
" optimizer.zero_grad()\n",
"\n",
" # 4. Loss backward\n",
" loss.backward()\n",
"\n",
" # 5. Optimizer step\n",
" optimizer.step()\n",
"\n",
" # Calculate loss and accuracy per epoch and print out what's happening\n",
" train_loss /= len(data_loader)\n",
" train_acc /= len(data_loader)\n",
" print(f\"Train loss: {train_loss:.5f} | Train accuracy: {train_acc:.2f}%\")\n",
"\n",
"def test_step(data_loader: torch.utils.data.DataLoader,\n",
" model: torch.nn.Module,\n",
" loss_fn: torch.nn.Module,\n",
" accuracy_fn,\n",
" device: torch.device = device):\n",
" test_loss, test_acc = 0, 0\n",
" model.to(device)\n",
" model.eval() # put model in eval mode\n",
" # Turn on inference context manager\n",
" with torch.inference_mode(): \n",
" for X, y in data_loader:\n",
" # Send data to GPU\n",
" X, y = X.to(device), y.to(device)\n",
" \n",
" # 1. Forward pass\n",
" test_pred = model(X)\n",
" \n",
" # 2. Calculate loss and accuracy\n",
" test_loss += loss_fn(test_pred, y)\n",
" test_acc += accuracy_fn(y_true=y,\n",
" y_pred=test_pred.argmax(dim=1) # Go from logits -> pred labels\n",
" )\n",
" \n",
" # Adjust metrics and print out\n",
" test_loss /= len(data_loader)\n",
" test_acc /= len(data_loader)\n",
" print(f\"Test loss: {test_loss:.5f} | Test accuracy: {test_acc:.2f}%\\n\")"
]
},
{
"cell_type": "markdown",
"id": "e44121b6-c4be-4909-9175-dc9bd8dc6273",
"metadata": {
"id": "e44121b6-c4be-4909-9175-dc9bd8dc6273"
},
"source": [
"Woohoo!\n",
"\n",
"Now we've got some functions for training and testing our model, let's run them.\n",
"\n",
"We'll do so inside another loop for each epoch.\n",
"\n",
"That way for each epoch we're going a training and a testing step.\n",
"\n",
"> **Note:** You can customize how often you do a testing step. Sometimes people do them every five epochs or 10 epochs or in our case, every epoch.\n",
"\n",
"Let's also time things to see how long our code takes to run on the GPU."
]
},
{
"cell_type": "code",
"execution_count": 26,
"id": "2bb8094b-01a0-4b84-9526-ba8888d04901",
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/",
"height": 327,
"referenced_widgets": [
"3ee8f4a32dae40a2954869aa28d511af",
"9bdbfed6aaa64648ac9624541a719134",
"a7e31e6725a0417495bb5d8d9bb0eedb",
"8a07bf3a83cf44b09ebec23372699dd4",
"4da7f6dcecfc44928a784709a2f85c67",
"85241944b82749bda4b5b6ff50f484b2",
"b139c87d10be44229d2f65d356912c25",
"b684374f8a3c41cb887142dd2c4a0c94",
"325e5b7b95db4289b3ee1bd6dbfc4a6c",
"987db9e4bab746ff9d393aa1409cf628",
"dd5dcc8d0c424965ba5a329efbf725cc"
]
},
"id": "2bb8094b-01a0-4b84-9526-ba8888d04901",
"outputId": "83769d2d-6f3b-4704-e443-cfc4ef52cc81"
},
"outputs": [
{
"data": {
"application/vnd.jupyter.widget-view+json": {
"model_id": "3ee8f4a32dae40a2954869aa28d511af",
"version_major": 2,
"version_minor": 0
},
"text/plain": [
" 0%| | 0/3 [00:00 **Note:** The training time on CUDA vs CPU will depend largely on the quality of the CPU/GPU you're using. Read on for a more explained answer.\n",
"\n",
"> **Question:** \"I used a a GPU but my model didn't train faster, why might that be?\"\n",
">\n",
"> **Answer:** Well, one reason could be because your dataset and model are both so small (like the dataset and model we're working with) the benefits of using a GPU are outweighed by the time it actually takes to transfer the data there.\n",
"> \n",
"> There's a small bottleneck between copying data from the CPU memory (default) to the GPU memory.\n",
">\n",
"> So for smaller models and datasets, the CPU might actually be the optimal place to compute on.\n",
">\n",
"> But for larger datasets and models, the speed of computing the GPU can offer usually far outweighs the cost of getting the data there.\n",
">\n",
"> However, this is largely dependant on the hardware you're using. With practice, you will get used to where the best place to train your models is. \n",
"\n",
"Let's evaluate our trained `model_1` using our `eval_model()` function and see how it went."
]
},
{
"cell_type": "code",
"execution_count": 27,
"id": "32a544e3-9dbe-4aa1-b074-22e28b8f2f2a",
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/",
"height": 381
},
"id": "32a544e3-9dbe-4aa1-b074-22e28b8f2f2a",
"outputId": "bab29648-1e35-4f01-9efe-fa4d2030cddb"
},
"outputs": [
{
"ename": "RuntimeError",
"evalue": "ignored",
"output_type": "error",
"traceback": [
"\u001b[0;31m---------------------------------------------------------------------------\u001b[0m",
"\u001b[0;31mRuntimeError\u001b[0m Traceback (most recent call last)",
"\u001b[0;32m\u001b[0m in \u001b[0;36m\u001b[0;34m()\u001b[0m\n\u001b[1;32m 2\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 3\u001b[0m \u001b[0;31m# Note: This will error due to `eval_model()` not using device agnostic code\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m----> 4\u001b[0;31m model_1_results = eval_model(model=model_1, \n\u001b[0m\u001b[1;32m 5\u001b[0m \u001b[0mdata_loader\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mtest_dataloader\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 6\u001b[0m \u001b[0mloss_fn\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mloss_fn\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32m\u001b[0m in \u001b[0;36meval_model\u001b[0;34m(model, data_loader, loss_fn, accuracy_fn)\u001b[0m\n\u001b[1;32m 20\u001b[0m \u001b[0;32mfor\u001b[0m \u001b[0mX\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0my\u001b[0m \u001b[0;32min\u001b[0m \u001b[0mdata_loader\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 21\u001b[0m \u001b[0;31m# Make predictions with the model\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m---> 22\u001b[0;31m \u001b[0my_pred\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mmodel\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mX\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 23\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 24\u001b[0m \u001b[0;31m# Accumulate the loss and accuracy values per batch\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32m/usr/local/lib/python3.10/dist-packages/torch/nn/modules/module.py\u001b[0m in \u001b[0;36m_call_impl\u001b[0;34m(self, *args, **kwargs)\u001b[0m\n\u001b[1;32m 1499\u001b[0m \u001b[0;32mor\u001b[0m \u001b[0m_global_backward_pre_hooks\u001b[0m \u001b[0;32mor\u001b[0m \u001b[0m_global_backward_hooks\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 1500\u001b[0m or _global_forward_hooks or _global_forward_pre_hooks):\n\u001b[0;32m-> 1501\u001b[0;31m \u001b[0;32mreturn\u001b[0m \u001b[0mforward_call\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34m*\u001b[0m\u001b[0margs\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0;34m**\u001b[0m\u001b[0mkwargs\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 1502\u001b[0m \u001b[0;31m# Do not call functions when jit is used\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 1503\u001b[0m \u001b[0mfull_backward_hooks\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mnon_full_backward_hooks\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0;34m[\u001b[0m\u001b[0;34m]\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0;34m[\u001b[0m\u001b[0;34m]\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32m\u001b[0m in \u001b[0;36mforward\u001b[0;34m(self, x)\u001b[0m\n\u001b[1;32m 12\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 13\u001b[0m \u001b[0;32mdef\u001b[0m \u001b[0mforward\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mself\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mx\u001b[0m\u001b[0;34m:\u001b[0m \u001b[0mtorch\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mTensor\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m---> 14\u001b[0;31m \u001b[0;32mreturn\u001b[0m \u001b[0mself\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mlayer_stack\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mx\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m",
"\u001b[0;32m/usr/local/lib/python3.10/dist-packages/torch/nn/modules/module.py\u001b[0m in \u001b[0;36m_call_impl\u001b[0;34m(self, *args, **kwargs)\u001b[0m\n\u001b[1;32m 1499\u001b[0m \u001b[0;32mor\u001b[0m \u001b[0m_global_backward_pre_hooks\u001b[0m \u001b[0;32mor\u001b[0m \u001b[0m_global_backward_hooks\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 1500\u001b[0m or _global_forward_hooks or _global_forward_pre_hooks):\n\u001b[0;32m-> 1501\u001b[0;31m \u001b[0;32mreturn\u001b[0m \u001b[0mforward_call\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34m*\u001b[0m\u001b[0margs\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0;34m**\u001b[0m\u001b[0mkwargs\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 1502\u001b[0m \u001b[0;31m# Do not call functions when jit is used\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 1503\u001b[0m \u001b[0mfull_backward_hooks\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mnon_full_backward_hooks\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0;34m[\u001b[0m\u001b[0;34m]\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0;34m[\u001b[0m\u001b[0;34m]\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32m/usr/local/lib/python3.10/dist-packages/torch/nn/modules/container.py\u001b[0m in \u001b[0;36mforward\u001b[0;34m(self, input)\u001b[0m\n\u001b[1;32m 215\u001b[0m \u001b[0;32mdef\u001b[0m \u001b[0mforward\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mself\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0minput\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 216\u001b[0m \u001b[0;32mfor\u001b[0m \u001b[0mmodule\u001b[0m \u001b[0;32min\u001b[0m \u001b[0mself\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m--> 217\u001b[0;31m \u001b[0minput\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mmodule\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0minput\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 218\u001b[0m \u001b[0;32mreturn\u001b[0m \u001b[0minput\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 219\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32m/usr/local/lib/python3.10/dist-packages/torch/nn/modules/module.py\u001b[0m in \u001b[0;36m_call_impl\u001b[0;34m(self, *args, **kwargs)\u001b[0m\n\u001b[1;32m 1499\u001b[0m \u001b[0;32mor\u001b[0m \u001b[0m_global_backward_pre_hooks\u001b[0m \u001b[0;32mor\u001b[0m \u001b[0m_global_backward_hooks\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 1500\u001b[0m or _global_forward_hooks or _global_forward_pre_hooks):\n\u001b[0;32m-> 1501\u001b[0;31m \u001b[0;32mreturn\u001b[0m \u001b[0mforward_call\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34m*\u001b[0m\u001b[0margs\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0;34m**\u001b[0m\u001b[0mkwargs\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 1502\u001b[0m \u001b[0;31m# Do not call functions when jit is used\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 1503\u001b[0m \u001b[0mfull_backward_hooks\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mnon_full_backward_hooks\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0;34m[\u001b[0m\u001b[0;34m]\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0;34m[\u001b[0m\u001b[0;34m]\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32m/usr/local/lib/python3.10/dist-packages/torch/nn/modules/linear.py\u001b[0m in \u001b[0;36mforward\u001b[0;34m(self, input)\u001b[0m\n\u001b[1;32m 112\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 113\u001b[0m \u001b[0;32mdef\u001b[0m \u001b[0mforward\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mself\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0minput\u001b[0m\u001b[0;34m:\u001b[0m \u001b[0mTensor\u001b[0m\u001b[0;34m)\u001b[0m \u001b[0;34m->\u001b[0m \u001b[0mTensor\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m--> 114\u001b[0;31m \u001b[0;32mreturn\u001b[0m \u001b[0mF\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mlinear\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0minput\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mself\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mweight\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mself\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mbias\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 115\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 116\u001b[0m \u001b[0;32mdef\u001b[0m \u001b[0mextra_repr\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mself\u001b[0m\u001b[0;34m)\u001b[0m \u001b[0;34m->\u001b[0m \u001b[0mstr\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;31mRuntimeError\u001b[0m: Expected all tensors to be on the same device, but found at least two devices, cuda:0 and cpu! (when checking argument for argument mat1 in method wrapper_CUDA_addmm)"
]
}
],
"source": [
"torch.manual_seed(42)\n",
"\n",
"# Note: This will error due to `eval_model()` not using device agnostic code \n",
"model_1_results = eval_model(model=model_1, \n",
" data_loader=test_dataloader,\n",
" loss_fn=loss_fn, \n",
" accuracy_fn=accuracy_fn) \n",
"model_1_results "
]
},
{
"cell_type": "markdown",
"id": "6a3481a5-489d-4db9-ac95-c3ce385978b7",
"metadata": {
"id": "6a3481a5-489d-4db9-ac95-c3ce385978b7"
},
"source": [
"Oh no! \n",
"\n",
"It looks like our `eval_model()` function errors out with:\n",
"\n",
"> `RuntimeError: Expected all tensors to be on the same device, but found at least two devices, cuda:0 and cpu! (when checking argument for argument mat1 in method wrapper_addmm)`\n",
"\n",
"It's because we've setup our data and model to use device-agnostic code but not our evaluation function.\n",
"\n",
"How about we fix that by passing a target `device` parameter to our `eval_model()` function?\n",
"\n",
"Then we'll try calculating the results again."
]
},
{
"cell_type": "code",
"execution_count": 28,
"id": "f3665d99-1adc-4d9f-bfc6-e5601a80691c",
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/"
},
"id": "f3665d99-1adc-4d9f-bfc6-e5601a80691c",
"outputId": "05312922-d30b-4c09-9989-963a4a579bf8"
},
"outputs": [
{
"data": {
"text/plain": [
"{'model_name': 'FashionMNISTModelV1',\n",
" 'model_loss': 0.6850008964538574,\n",
" 'model_acc': 75.01996805111821}"
]
},
"execution_count": 28,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Move values to device\n",
"torch.manual_seed(42)\n",
"def eval_model(model: torch.nn.Module, \n",
" data_loader: torch.utils.data.DataLoader, \n",
" loss_fn: torch.nn.Module, \n",
" accuracy_fn, \n",
" device: torch.device = device):\n",
" \"\"\"Evaluates a given model on a given dataset.\n",
"\n",
" Args:\n",
" model (torch.nn.Module): A PyTorch model capable of making predictions on data_loader.\n",
" data_loader (torch.utils.data.DataLoader): The target dataset to predict on.\n",
" loss_fn (torch.nn.Module): The loss function of model.\n",
" accuracy_fn: An accuracy function to compare the models predictions to the truth labels.\n",
" device (str, optional): Target device to compute on. Defaults to device.\n",
"\n",
" Returns:\n",
" (dict): Results of model making predictions on data_loader.\n",
" \"\"\"\n",
" loss, acc = 0, 0\n",
" model.eval()\n",
" with torch.inference_mode():\n",
" for X, y in data_loader:\n",
" # Send data to the target device\n",
" X, y = X.to(device), y.to(device)\n",
" y_pred = model(X)\n",
" loss += loss_fn(y_pred, y)\n",
" acc += accuracy_fn(y_true=y, y_pred=y_pred.argmax(dim=1))\n",
" \n",
" # Scale loss and acc\n",
" loss /= len(data_loader)\n",
" acc /= len(data_loader)\n",
" return {\"model_name\": model.__class__.__name__, # only works when model was created with a class\n",
" \"model_loss\": loss.item(),\n",
" \"model_acc\": acc}\n",
"\n",
"# Calculate model 1 results with device-agnostic code \n",
"model_1_results = eval_model(model=model_1, data_loader=test_dataloader,\n",
" loss_fn=loss_fn, accuracy_fn=accuracy_fn,\n",
" device=device\n",
")\n",
"model_1_results"
]
},
{
"cell_type": "code",
"execution_count": 29,
"id": "a9e916cf-f873-4481-a983-bac26ce4cac2",
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/"
},
"id": "a9e916cf-f873-4481-a983-bac26ce4cac2",
"outputId": "5cdb9f7f-366c-4c14-9afa-f2d1d4e0267d"
},
"outputs": [
{
"data": {
"text/plain": [
"{'model_name': 'FashionMNISTModelV0',\n",
" 'model_loss': 0.47663894295692444,\n",
" 'model_acc': 83.42651757188499}"
]
},
"execution_count": 29,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Check baseline results\n",
"model_0_results"
]
},
{
"cell_type": "markdown",
"id": "340cbf14-e83f-4981-8a93-5fedb6b51418",
"metadata": {
"id": "340cbf14-e83f-4981-8a93-5fedb6b51418"
},
"source": [
"Woah, in this case, it looks like adding non-linearities to our model made it perform worse than the baseline.\n",
"\n",
"That's a thing to note in machine learning, sometimes the thing you thought should work doesn't. \n",
"\n",
"And then the thing you thought might not work does.\n",
"\n",
"It's part science, part art.\n",
"\n",
"From the looks of things, it seems like our model is **overfitting** on the training data.\n",
"\n",
"Overfitting means our model is learning the training data well but those patterns aren't generalizing to the testing data.\n",
"\n",
"Two of the main to fix overfitting include:\n",
"1. Using a smaller or different model (some models fit certain kinds of data better than others).\n",
"2. Using a larger dataset (the more data, the more chance a model has to learn generalizable patterns).\n",
"\n",
"There are more, but I'm going to leave that as a challenge for you to explore.\n",
"\n",
"Try searching online, \"ways to prevent overfitting in machine learning\" and see what comes up.\n",
"\n",
"In the meantime, let's take a look at number 1: using a different model."
]
},
{
"cell_type": "markdown",
"id": "ac22d685-1b8d-4215-90de-c0476cb0fbdf",
"metadata": {
"id": "ac22d685-1b8d-4215-90de-c0476cb0fbdf"
},
"source": [
"## 7. Model 2: Building a Convolutional Neural Network (CNN)\n",
"\n",
"Alright, time to step things up a notch.\n",
"\n",
"It's time to create a [Convolutional Neural Network](https://en.wikipedia.org/wiki/Convolutional_neural_network) (CNN or ConvNet).\n",
"\n",
"CNN's are known for their capabilities to find patterns in visual data.\n",
"\n",
"And since we're dealing with visual data, let's see if using a CNN model can improve upon our baseline.\n",
"\n",
"The CNN model we're going to be using is known as TinyVGG from the [CNN Explainer](https://poloclub.github.io/cnn-explainer/) website.\n",
"\n",
"It follows the typical structure of a convolutional neural network:\n",
"\n",
"`Input layer -> [Convolutional layer -> activation layer -> pooling layer] -> Output layer`\n",
"\n",
"Where the contents of `[Convolutional layer -> activation layer -> pooling layer]` can be upscaled and repeated multiple times, depending on requirements. "
]
},
{
"cell_type": "markdown",
"id": "9c358955-1d20-4903-b872-a239d2753d88",
"metadata": {
"id": "9c358955-1d20-4903-b872-a239d2753d88"
},
"source": [
"### What model should I use?\n",
"\n",
"> **Question:** Wait, you say CNN's are good for images, are there any other model types I should be aware of?\n",
"\n",
"Good question.\n",
"\n",
"This table is a good general guide for which model to use (though there are exceptions).\n",
"\n",
"| **Problem type** | **Model to use (generally)** | **Code example** |\n",
"| ----- | ----- | ----- |\n",
"| Structured data (Excel spreadsheets, row and column data) | Gradient boosted models, Random Forests, XGBoost | [`sklearn.ensemble`](https://scikit-learn.org/stable/modules/classes.html#module-sklearn.ensemble), [XGBoost library](https://xgboost.readthedocs.io/en/stable/) |\n",
"| Unstructured data (images, audio, language) | Convolutional Neural Networks, Transformers | [`torchvision.models`](https://pytorch.org/vision/stable/models.html), [HuggingFace Transformers](https://huggingface.co/docs/transformers/index) | \n",
"\n",
"> **Note:** The table above is only for reference, the model you end up using will be highly dependant on the problem you're working on and the constraints you have (amount of data, latency requirements).\n",
"\n",
"Enough talking about models, let's now build a CNN that replicates the model on the [CNN Explainer website](https://poloclub.github.io/cnn-explainer/).\n",
"\n",
"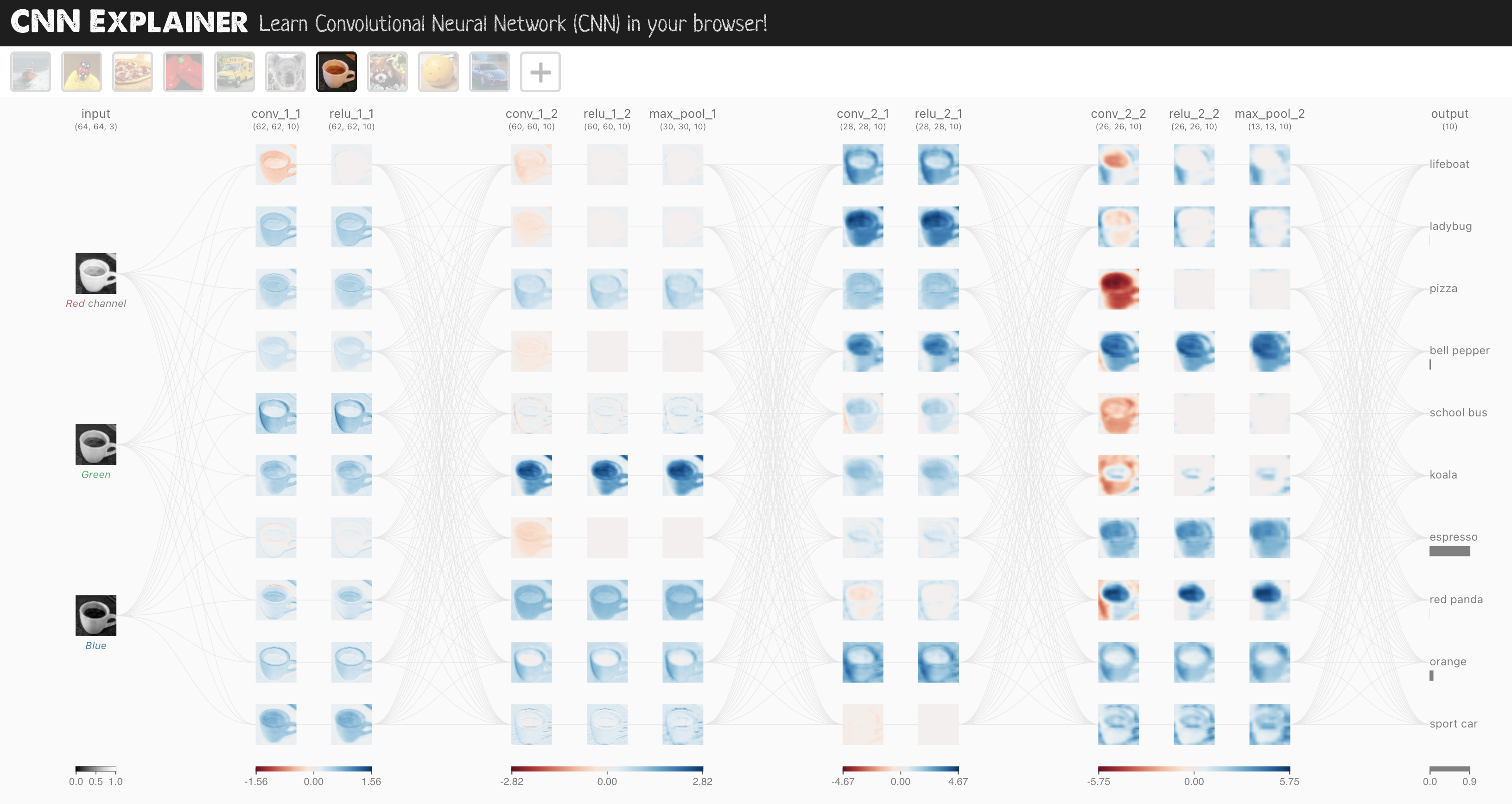\n",
"\n",
"To do so, we'll leverage the [`nn.Conv2d()`](https://pytorch.org/docs/stable/generated/torch.nn.Conv2d.html) and [`nn.MaxPool2d()`](https://pytorch.org/docs/stable/generated/torch.nn.MaxPool2d.html) layers from `torch.nn`.\n"
]
},
{
"cell_type": "code",
"execution_count": 30,
"id": "dce60214-63fd-46e2-89ba-125445ac76b7",
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/"
},
"id": "dce60214-63fd-46e2-89ba-125445ac76b7",
"outputId": "5ae97191-bb41-4e58-e7f1-914b612cbb60"
},
"outputs": [
{
"data": {
"text/plain": [
"FashionMNISTModelV2(\n",
" (block_1): Sequential(\n",
" (0): Conv2d(1, 10, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))\n",
" (1): ReLU()\n",
" (2): Conv2d(10, 10, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))\n",
" (3): ReLU()\n",
" (4): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)\n",
" )\n",
" (block_2): Sequential(\n",
" (0): Conv2d(10, 10, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))\n",
" (1): ReLU()\n",
" (2): Conv2d(10, 10, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))\n",
" (3): ReLU()\n",
" (4): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)\n",
" )\n",
" (classifier): Sequential(\n",
" (0): Flatten(start_dim=1, end_dim=-1)\n",
" (1): Linear(in_features=490, out_features=10, bias=True)\n",
" )\n",
")"
]
},
"execution_count": 30,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Create a convolutional neural network \n",
"class FashionMNISTModelV2(nn.Module):\n",
" \"\"\"\n",
" Model architecture copying TinyVGG from: \n",
" https://poloclub.github.io/cnn-explainer/\n",
" \"\"\"\n",
" def __init__(self, input_shape: int, hidden_units: int, output_shape: int):\n",
" super().__init__()\n",
" self.block_1 = nn.Sequential(\n",
" nn.Conv2d(in_channels=input_shape, \n",
" out_channels=hidden_units, \n",
" kernel_size=3, # how big is the square that's going over the image?\n",
" stride=1, # default\n",
" padding=1),# options = \"valid\" (no padding) or \"same\" (output has same shape as input) or int for specific number \n",
" nn.ReLU(),\n",
" nn.Conv2d(in_channels=hidden_units, \n",
" out_channels=hidden_units,\n",
" kernel_size=3,\n",
" stride=1,\n",
" padding=1),\n",
" nn.ReLU(),\n",
" nn.MaxPool2d(kernel_size=2,\n",
" stride=2) # default stride value is same as kernel_size\n",
" )\n",
" self.block_2 = nn.Sequential(\n",
" nn.Conv2d(hidden_units, hidden_units, 3, padding=1),\n",
" nn.ReLU(),\n",
" nn.Conv2d(hidden_units, hidden_units, 3, padding=1),\n",
" nn.ReLU(),\n",
" nn.MaxPool2d(2)\n",
" )\n",
" self.classifier = nn.Sequential(\n",
" nn.Flatten(),\n",
" # Where did this in_features shape come from? \n",
" # It's because each layer of our network compresses and changes the shape of our inputs data.\n",
" nn.Linear(in_features=hidden_units*7*7, \n",
" out_features=output_shape)\n",
" )\n",
" \n",
" def forward(self, x: torch.Tensor):\n",
" x = self.block_1(x)\n",
" # print(x.shape)\n",
" x = self.block_2(x)\n",
" # print(x.shape)\n",
" x = self.classifier(x)\n",
" # print(x.shape)\n",
" return x\n",
"\n",
"torch.manual_seed(42)\n",
"model_2 = FashionMNISTModelV2(input_shape=1, \n",
" hidden_units=10, \n",
" output_shape=len(class_names)).to(device)\n",
"model_2"
]
},
{
"cell_type": "markdown",
"id": "0a20f25e-cc16-4f85-a69b-62008c01d0ed",
"metadata": {
"id": "0a20f25e-cc16-4f85-a69b-62008c01d0ed"
},
"source": [
"Nice!\n",
"\n",
"Our biggest model yet!\n",
"\n",
"What we've done is a common practice in machine learning.\n",
"\n",
"Find a model architecture somewhere and replicate it with code. "
]
},
{
"cell_type": "markdown",
"id": "6478cc5a-7b33-425d-9ab3-6d40168a1aee",
"metadata": {
"id": "6478cc5a-7b33-425d-9ab3-6d40168a1aee"
},
"source": [
"### 7.1 Stepping through `nn.Conv2d()`\n",
"\n",
"We could start using our model above and see what happens but let's first step through the two new layers we've added:\n",
"* [`nn.Conv2d()`](https://pytorch.org/docs/stable/generated/torch.nn.Conv2d.html), also known as a convolutional layer.\n",
"* [`nn.MaxPool2d()`](https://pytorch.org/docs/stable/generated/torch.nn.MaxPool2d.html), also known as a max pooling layer.\n",
"\n",
"> **Question:** What does the \"2d\" in `nn.Conv2d()` stand for?\n",
">\n",
"> The 2d is for 2-dimensional data. As in, our images have two dimensions: height and width. Yes, there's color channel dimension but each of the color channel dimensions have two dimensions too: height and width.\n",
">\n",
"> For other dimensional data (such as 1D for text or 3D for 3D objects) there's also `nn.Conv1d()` and `nn.Conv3d()`. \n",
"\n",
"To test the layers out, let's create some toy data just like the data used on CNN Explainer."
]
},
{
"cell_type": "code",
"execution_count": 31,
"id": "058b01ac-3f6a-4472-bcbf-3377974e3254",
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/"
},
"id": "058b01ac-3f6a-4472-bcbf-3377974e3254",
"outputId": "c404a8dd-d804-4993-bc2b-e4fdbf02b62d"
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Image batch shape: torch.Size([32, 3, 64, 64]) -> [batch_size, color_channels, height, width]\n",
"Single image shape: torch.Size([3, 64, 64]) -> [color_channels, height, width]\n",
"Single image pixel values:\n",
"tensor([[[ 1.9269, 1.4873, 0.9007, ..., 1.8446, -1.1845, 1.3835],\n",
" [ 1.4451, 0.8564, 2.2181, ..., 0.3399, 0.7200, 0.4114],\n",
" [ 1.9312, 1.0119, -1.4364, ..., -0.5558, 0.7043, 0.7099],\n",
" ...,\n",
" [-0.5610, -0.4830, 0.4770, ..., -0.2713, -0.9537, -0.6737],\n",
" [ 0.3076, -0.1277, 0.0366, ..., -2.0060, 0.2824, -0.8111],\n",
" [-1.5486, 0.0485, -0.7712, ..., -0.1403, 0.9416, -0.0118]],\n",
"\n",
" [[-0.5197, 1.8524, 1.8365, ..., 0.8935, -1.5114, -0.8515],\n",
" [ 2.0818, 1.0677, -1.4277, ..., 1.6612, -2.6223, -0.4319],\n",
" [-0.1010, -0.4388, -1.9775, ..., 0.2106, 0.2536, -0.7318],\n",
" ...,\n",
" [ 0.2779, 0.7342, -0.3736, ..., -0.4601, 0.1815, 0.1850],\n",
" [ 0.7205, -0.2833, 0.0937, ..., -0.1002, -2.3609, 2.2465],\n",
" [-1.3242, -0.1973, 0.2920, ..., 0.5409, 0.6940, 1.8563]],\n",
"\n",
" [[-0.7978, 1.0261, 1.1465, ..., 1.2134, 0.9354, -0.0780],\n",
" [-1.4647, -1.9571, 0.1017, ..., -1.9986, -0.7409, 0.7011],\n",
" [-1.3938, 0.8466, -1.7191, ..., -1.1867, 0.1320, 0.3407],\n",
" ...,\n",
" [ 0.8206, -0.3745, 1.2499, ..., -0.0676, 0.0385, 0.6335],\n",
" [-0.5589, -0.3393, 0.2347, ..., 2.1181, 2.4569, 1.3083],\n",
" [-0.4092, 1.5199, 0.2401, ..., -0.2558, 0.7870, 0.9924]]])\n"
]
}
],
"source": [
"torch.manual_seed(42)\n",
"\n",
"# Create sample batch of random numbers with same size as image batch\n",
"images = torch.randn(size=(32, 3, 64, 64)) # [batch_size, color_channels, height, width]\n",
"test_image = images[0] # get a single image for testing\n",
"print(f\"Image batch shape: {images.shape} -> [batch_size, color_channels, height, width]\")\n",
"print(f\"Single image shape: {test_image.shape} -> [color_channels, height, width]\") \n",
"print(f\"Single image pixel values:\\n{test_image}\")"
]
},
{
"cell_type": "markdown",
"id": "bd3291c2-854e-4d0c-97b9-8bf46085fc43",
"metadata": {
"id": "bd3291c2-854e-4d0c-97b9-8bf46085fc43"
},
"source": [
"Let's create an example `nn.Conv2d()` with various parameters:\n",
"* `in_channels` (int) - Number of channels in the input image.\n",
"* `out_channels` (int) - Number of channels produced by the convolution.\n",
"* `kernel_size` (int or tuple) - Size of the convolving kernel/filter.\n",
"* `stride` (int or tuple, optional) - How big of a step the convolving kernel takes at a time. Default: 1.\n",
"* `padding` (int, tuple, str) - Padding added to all four sides of input. Default: 0.\n",
"\n",
"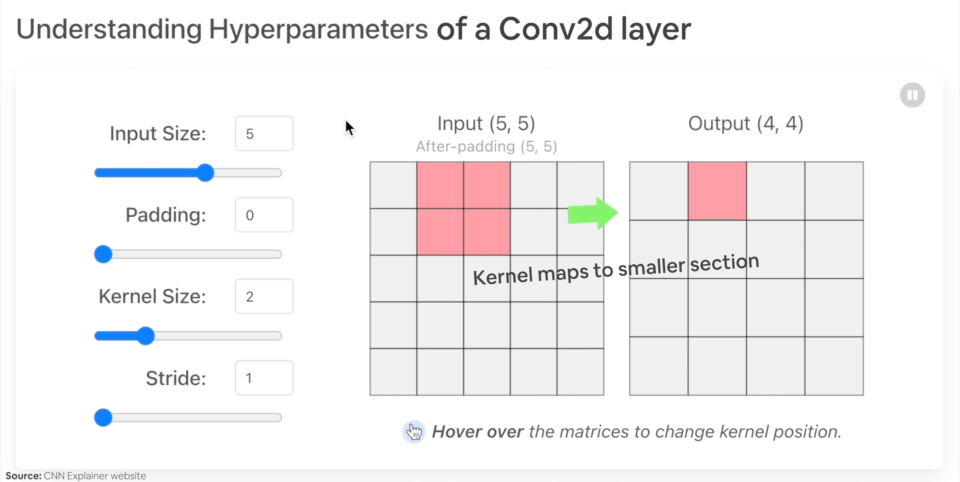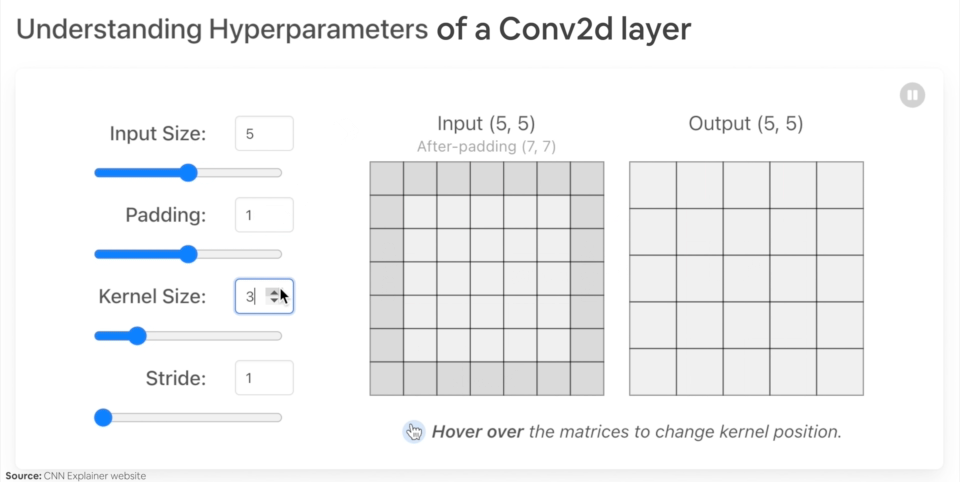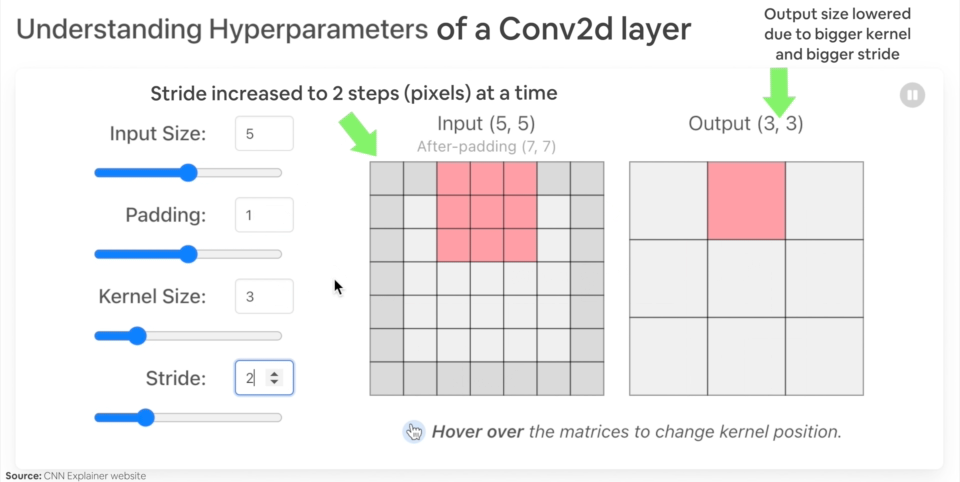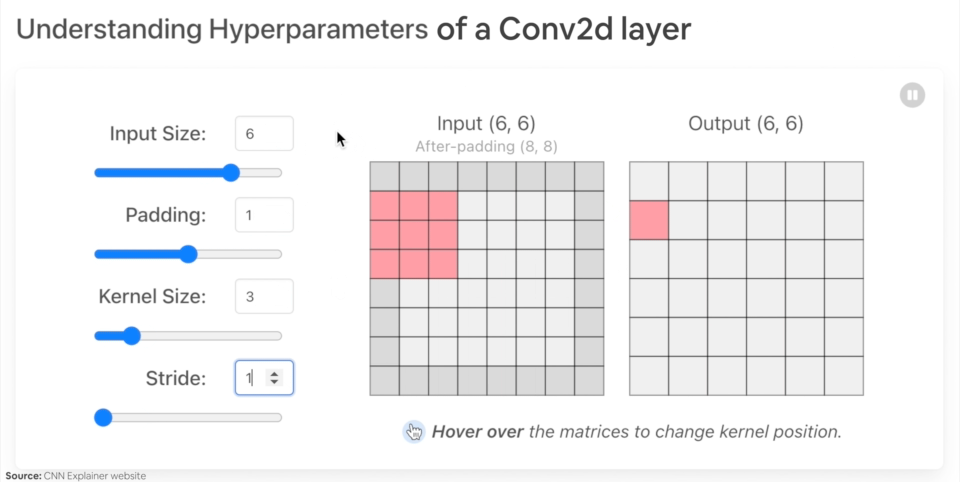\n",
"\n",
"*Example of what happens when you change the hyperparameters of a `nn.Conv2d()` layer.*"
]
},
{
"cell_type": "code",
"execution_count": 32,
"id": "ebd39562-1dad-40e3-90f5-750a5dac24e2",
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/"
},
"id": "ebd39562-1dad-40e3-90f5-750a5dac24e2",
"outputId": "b61154fb-c5f7-4c3f-c619-4bde6edb4d16"
},
"outputs": [
{
"data": {
"text/plain": [
"tensor([[[ 1.5396, 0.0516, 0.6454, ..., -0.3673, 0.8711, 0.4256],\n",
" [ 0.3662, 1.0114, -0.5997, ..., 0.8983, 0.2809, -0.2741],\n",
" [ 1.2664, -1.4054, 0.3727, ..., -0.3409, 1.2191, -0.0463],\n",
" ...,\n",
" [-0.1541, 0.5132, -0.3624, ..., -0.2360, -0.4609, -0.0035],\n",
" [ 0.2981, -0.2432, 1.5012, ..., -0.6289, -0.7283, -0.5767],\n",
" [-0.0386, -0.0781, -0.0388, ..., 0.2842, 0.4228, -0.1802]],\n",
"\n",
" [[-0.2840, -0.0319, -0.4455, ..., -0.7956, 1.5599, -1.2449],\n",
" [ 0.2753, -0.1262, -0.6541, ..., -0.2211, 0.1999, -0.8856],\n",
" [-0.5404, -1.5489, 0.0249, ..., -0.5932, -1.0913, -0.3849],\n",
" ...,\n",
" [ 0.3870, -0.4064, -0.8236, ..., 0.1734, -0.4330, -0.4951],\n",
" [-0.1984, -0.6386, 1.0263, ..., -0.9401, -0.0585, -0.7833],\n",
" [-0.6306, -0.2052, -0.3694, ..., -1.3248, 0.2456, -0.7134]],\n",
"\n",
" [[ 0.4414, 0.5100, 0.4846, ..., -0.8484, 0.2638, 1.1258],\n",
" [ 0.8117, 0.3191, -0.0157, ..., 1.2686, 0.2319, 0.5003],\n",
" [ 0.3212, 0.0485, -0.2581, ..., 0.2258, 0.2587, -0.8804],\n",
" ...,\n",
" [-0.1144, -0.1869, 0.0160, ..., -0.8346, 0.0974, 0.8421],\n",
" [ 0.2941, 0.4417, 0.5866, ..., -0.1224, 0.4814, -0.4799],\n",
" [ 0.6059, -0.0415, -0.2028, ..., 0.1170, 0.2521, -0.4372]],\n",
"\n",
" ...,\n",
"\n",
" [[-0.2560, -0.0477, 0.6380, ..., 0.6436, 0.7553, -0.7055],\n",
" [ 1.5595, -0.2209, -0.9486, ..., -0.4876, 0.7754, 0.0750],\n",
" [-0.0797, 0.2471, 1.1300, ..., 0.1505, 0.2354, 0.9576],\n",
" ...,\n",
" [ 1.1065, 0.6839, 1.2183, ..., 0.3015, -0.1910, -0.1902],\n",
" [-0.3486, -0.7173, -0.3582, ..., 0.4917, 0.7219, 0.1513],\n",
" [ 0.0119, 0.1017, 0.7839, ..., -0.3752, -0.8127, -0.1257]],\n",
"\n",
" [[ 0.3841, 1.1322, 0.1620, ..., 0.7010, 0.0109, 0.6058],\n",
" [ 0.1664, 0.1873, 1.5924, ..., 0.3733, 0.9096, -0.5399],\n",
" [ 0.4094, -0.0861, -0.7935, ..., -0.1285, -0.9932, -0.3013],\n",
" ...,\n",
" [ 0.2688, -0.5630, -1.1902, ..., 0.4493, 0.5404, -0.0103],\n",
" [ 0.0535, 0.4411, 0.5313, ..., 0.0148, -1.0056, 0.3759],\n",
" [ 0.3031, -0.1590, -0.1316, ..., -0.5384, -0.4271, -0.4876]],\n",
"\n",
" [[-1.1865, -0.7280, -1.2331, ..., -0.9013, -0.0542, -1.5949],\n",
" [-0.6345, -0.5920, 0.5326, ..., -1.0395, -0.7963, -0.0647],\n",
" [-0.1132, 0.5166, 0.2569, ..., 0.5595, -1.6881, 0.9485],\n",
" ...,\n",
" [-0.0254, -0.2669, 0.1927, ..., -0.2917, 0.1088, -0.4807],\n",
" [-0.2609, -0.2328, 0.1404, ..., -0.1325, -0.8436, -0.7524],\n",
" [-1.1399, -0.1751, -0.8705, ..., 0.1589, 0.3377, 0.3493]]],\n",
" grad_fn=)"
]
},
"execution_count": 32,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"torch.manual_seed(42)\n",
"\n",
"# Create a convolutional layer with same dimensions as TinyVGG \n",
"# (try changing any of the parameters and see what happens)\n",
"conv_layer = nn.Conv2d(in_channels=3,\n",
" out_channels=10,\n",
" kernel_size=3,\n",
" stride=1,\n",
" padding=0) # also try using \"valid\" or \"same\" here \n",
"\n",
"# Pass the data through the convolutional layer\n",
"conv_layer(test_image) # Note: If running PyTorch <1.11.0, this will error because of shape issues (nn.Conv.2d() expects a 4d tensor as input) "
]
},
{
"cell_type": "markdown",
"id": "cb0184ad-5c16-4e1c-bcfa-70ecf15377da",
"metadata": {
"id": "cb0184ad-5c16-4e1c-bcfa-70ecf15377da"
},
"source": [
"If we try to pass a single image in, we get a shape mismatch error:\n",
"\n",
"> `RuntimeError: Expected 4-dimensional input for 4-dimensional weight [10, 3, 3, 3], but got 3-dimensional input of size [3, 64, 64] instead`\n",
">\n",
"> **Note:** If you're running PyTorch 1.11.0+, this error won't occur.\n",
"\n",
"This is because our `nn.Conv2d()` layer expects a 4-dimensional tensor as input with size `(N, C, H, W)` or `[batch_size, color_channels, height, width]`.\n",
"\n",
"Right now our single image `test_image` only has a shape of `[color_channels, height, width]` or `[3, 64, 64]`.\n",
"\n",
"We can fix this for a single image using `test_image.unsqueeze(dim=0)` to add an extra dimension for `N`."
]
},
{
"cell_type": "code",
"execution_count": 33,
"id": "abba741d-a1ed-44ed-ba53-41d589433a2c",
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/"
},
"id": "abba741d-a1ed-44ed-ba53-41d589433a2c",
"outputId": "9dd8151d-376c-4342-c379-91fcb6468706"
},
"outputs": [
{
"data": {
"text/plain": [
"torch.Size([1, 3, 64, 64])"
]
},
"execution_count": 33,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Add extra dimension to test image\n",
"test_image.unsqueeze(dim=0).shape"
]
},
{
"cell_type": "code",
"execution_count": 34,
"id": "c7280a49-4ee0-452b-a514-61115b6a444c",
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/"
},
"id": "c7280a49-4ee0-452b-a514-61115b6a444c",
"outputId": "87bf7e37-c1a7-44a4-eef2-a02eb0489147"
},
"outputs": [
{
"data": {
"text/plain": [
"torch.Size([1, 10, 62, 62])"
]
},
"execution_count": 34,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Pass test image with extra dimension through conv_layer\n",
"conv_layer(test_image.unsqueeze(dim=0)).shape"
]
},
{
"cell_type": "markdown",
"id": "181df81b-7c5a-46cc-b8d5-a592bf755a13",
"metadata": {
"id": "181df81b-7c5a-46cc-b8d5-a592bf755a13"
},
"source": [
"Hmm, notice what happens to our shape (the same shape as the first layer of TinyVGG on [CNN Explainer](https://poloclub.github.io/cnn-explainer/)), we get different channel sizes as well as different pixel sizes.\n",
"\n",
"What if we changed the values of `conv_layer`?"
]
},
{
"cell_type": "code",
"execution_count": 35,
"id": "04445d45-cf2f-4c1d-b215-bc50865a207a",
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/"
},
"id": "04445d45-cf2f-4c1d-b215-bc50865a207a",
"outputId": "eaa97fb8-52c0-493d-eac3-f2e23df9b01c"
},
"outputs": [
{
"data": {
"text/plain": [
"torch.Size([1, 10, 30, 30])"
]
},
"execution_count": 35,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"torch.manual_seed(42)\n",
"# Create a new conv_layer with different values (try setting these to whatever you like)\n",
"conv_layer_2 = nn.Conv2d(in_channels=3, # same number of color channels as our input image\n",
" out_channels=10,\n",
" kernel_size=(5, 5), # kernel is usually a square so a tuple also works\n",
" stride=2,\n",
" padding=0)\n",
"\n",
"# Pass single image through new conv_layer_2 (this calls nn.Conv2d()'s forward() method on the input)\n",
"conv_layer_2(test_image.unsqueeze(dim=0)).shape"
]
},
{
"cell_type": "markdown",
"id": "b27dbdbb-3e32-4ffa-803e-cf943d96c72b",
"metadata": {
"id": "b27dbdbb-3e32-4ffa-803e-cf943d96c72b"
},
"source": [
"Woah, we get another shape change.\n",
"\n",
"Now our image is of shape `[1, 10, 30, 30]` (it will be different if you use different values) or `[batch_size=1, color_channels=10, height=30, width=30]`.\n",
"\n",
"What's going on here?\n",
"\n",
"Behind the scenes, our `nn.Conv2d()` is compressing the information stored in the image.\n",
"\n",
"It does this by performing operations on the input (our test image) against its internal parameters.\n",
"\n",
"The goal of this is similar to all of the other neural networks we've been building.\n",
"\n",
"Data goes in and the layers try to update their internal parameters (patterns) to lower the loss function thanks to some help of the optimizer.\n",
"\n",
"The only difference is *how* the different layers calculate their parameter updates or in PyTorch terms, the operation present in the layer `forward()` method.\n",
"\n",
"If we check out our `conv_layer_2.state_dict()` we'll find a similar weight and bias setup as we've seen before."
]
},
{
"cell_type": "code",
"execution_count": 36,
"id": "46027ed1-c3a7-46bd-bab7-17f8c20e354b",
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/"
},
"id": "46027ed1-c3a7-46bd-bab7-17f8c20e354b",
"outputId": "bc493b18-1ef3-41c6-9de9-5dfeaa4c259e"
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"OrderedDict([('weight', tensor([[[[ 0.0883, 0.0958, -0.0271, 0.1061, -0.0253],\n",
" [ 0.0233, -0.0562, 0.0678, 0.1018, -0.0847],\n",
" [ 0.1004, 0.0216, 0.0853, 0.0156, 0.0557],\n",
" [-0.0163, 0.0890, 0.0171, -0.0539, 0.0294],\n",
" [-0.0532, -0.0135, -0.0469, 0.0766, -0.0911]],\n",
"\n",
" [[-0.0532, -0.0326, -0.0694, 0.0109, -0.1140],\n",
" [ 0.1043, -0.0981, 0.0891, 0.0192, -0.0375],\n",
" [ 0.0714, 0.0180, 0.0933, 0.0126, -0.0364],\n",
" [ 0.0310, -0.0313, 0.0486, 0.1031, 0.0667],\n",
" [-0.0505, 0.0667, 0.0207, 0.0586, -0.0704]],\n",
"\n",
" [[-0.1143, -0.0446, -0.0886, 0.0947, 0.0333],\n",
" [ 0.0478, 0.0365, -0.0020, 0.0904, -0.0820],\n",
" [ 0.0073, -0.0788, 0.0356, -0.0398, 0.0354],\n",
" [-0.0241, 0.0958, -0.0684, -0.0689, -0.0689],\n",
" [ 0.1039, 0.0385, 0.1111, -0.0953, -0.1145]]],\n",
"\n",
"\n",
" [[[-0.0903, -0.0777, 0.0468, 0.0413, 0.0959],\n",
" [-0.0596, -0.0787, 0.0613, -0.0467, 0.0701],\n",
" [-0.0274, 0.0661, -0.0897, -0.0583, 0.0352],\n",
" [ 0.0244, -0.0294, 0.0688, 0.0785, -0.0837],\n",
" [-0.0616, 0.1057, -0.0390, -0.0409, -0.1117]],\n",
"\n",
" [[-0.0661, 0.0288, -0.0152, -0.0838, 0.0027],\n",
" [-0.0789, -0.0980, -0.0636, -0.1011, -0.0735],\n",
" [ 0.1154, 0.0218, 0.0356, -0.1077, -0.0758],\n",
" [-0.0384, 0.0181, -0.1016, -0.0498, -0.0691],\n",
" [ 0.0003, -0.0430, -0.0080, -0.0782, -0.0793]],\n",
"\n",
" [[-0.0674, -0.0395, -0.0911, 0.0968, -0.0229],\n",
" [ 0.0994, 0.0360, -0.0978, 0.0799, -0.0318],\n",
" [-0.0443, -0.0958, -0.1148, 0.0330, -0.0252],\n",
" [ 0.0450, -0.0948, 0.0857, -0.0848, -0.0199],\n",
" [ 0.0241, 0.0596, 0.0932, 0.1052, -0.0916]]],\n",
"\n",
"\n",
" [[[ 0.0291, -0.0497, -0.0127, -0.0864, 0.1052],\n",
" [-0.0847, 0.0617, 0.0406, 0.0375, -0.0624],\n",
" [ 0.1050, 0.0254, 0.0149, -0.1018, 0.0485],\n",
" [-0.0173, -0.0529, 0.0992, 0.0257, -0.0639],\n",
" [-0.0584, -0.0055, 0.0645, -0.0295, -0.0659]],\n",
"\n",
" [[-0.0395, -0.0863, 0.0412, 0.0894, -0.1087],\n",
" [ 0.0268, 0.0597, 0.0209, -0.0411, 0.0603],\n",
" [ 0.0607, 0.0432, -0.0203, -0.0306, 0.0124],\n",
" [-0.0204, -0.0344, 0.0738, 0.0992, -0.0114],\n",
" [-0.0259, 0.0017, -0.0069, 0.0278, 0.0324]],\n",
"\n",
" [[-0.1049, -0.0426, 0.0972, 0.0450, -0.0057],\n",
" [-0.0696, -0.0706, -0.1034, -0.0376, 0.0390],\n",
" [ 0.0736, 0.0533, -0.1021, -0.0694, -0.0182],\n",
" [ 0.1117, 0.0167, -0.0299, 0.0478, -0.0440],\n",
" [-0.0747, 0.0843, -0.0525, -0.0231, -0.1149]]],\n",
"\n",
"\n",
" [[[ 0.0773, 0.0875, 0.0421, -0.0805, -0.1140],\n",
" [-0.0938, 0.0861, 0.0554, 0.0972, 0.0605],\n",
" [ 0.0292, -0.0011, -0.0878, -0.0989, -0.1080],\n",
" [ 0.0473, -0.0567, -0.0232, -0.0665, -0.0210],\n",
" [-0.0813, -0.0754, 0.0383, -0.0343, 0.0713]],\n",
"\n",
" [[-0.0370, -0.0847, -0.0204, -0.0560, -0.0353],\n",
" [-0.1099, 0.0646, -0.0804, 0.0580, 0.0524],\n",
" [ 0.0825, -0.0886, 0.0830, -0.0546, 0.0428],\n",
" [ 0.1084, -0.0163, -0.0009, -0.0266, -0.0964],\n",
" [ 0.0554, -0.1146, 0.0717, 0.0864, 0.1092]],\n",
"\n",
" [[-0.0272, -0.0949, 0.0260, 0.0638, -0.1149],\n",
" [-0.0262, -0.0692, -0.0101, -0.0568, -0.0472],\n",
" [-0.0367, -0.1097, 0.0947, 0.0968, -0.0181],\n",
" [-0.0131, -0.0471, -0.1043, -0.1124, 0.0429],\n",
" [-0.0634, -0.0742, -0.0090, -0.0385, -0.0374]]],\n",
"\n",
"\n",
" [[[ 0.0037, -0.0245, -0.0398, -0.0553, -0.0940],\n",
" [ 0.0968, -0.0462, 0.0306, -0.0401, 0.0094],\n",
" [ 0.1077, 0.0532, -0.1001, 0.0458, 0.1096],\n",
" [ 0.0304, 0.0774, 0.1138, -0.0177, 0.0240],\n",
" [-0.0803, -0.0238, 0.0855, 0.0592, -0.0731]],\n",
"\n",
" [[-0.0926, -0.0789, -0.1140, -0.0891, -0.0286],\n",
" [ 0.0779, 0.0193, -0.0878, -0.0926, 0.0574],\n",
" [-0.0859, -0.0142, 0.0554, -0.0534, -0.0126],\n",
" [-0.0101, -0.0273, -0.0585, -0.1029, -0.0933],\n",
" [-0.0618, 0.1115, -0.0558, -0.0775, 0.0280]],\n",
"\n",
" [[ 0.0318, 0.0633, 0.0878, 0.0643, -0.1145],\n",
" [ 0.0102, 0.0699, -0.0107, -0.0680, 0.1101],\n",
" [-0.0432, -0.0657, -0.1041, 0.0052, 0.0512],\n",
" [ 0.0256, 0.0228, -0.0876, -0.1078, 0.0020],\n",
" [ 0.1053, 0.0666, -0.0672, -0.0150, -0.0851]]],\n",
"\n",
"\n",
" [[[-0.0557, 0.0209, 0.0629, 0.0957, -0.1060],\n",
" [ 0.0772, -0.0814, 0.0432, 0.0977, 0.0016],\n",
" [ 0.1051, -0.0984, -0.0441, 0.0673, -0.0252],\n",
" [-0.0236, -0.0481, 0.0796, 0.0566, 0.0370],\n",
" [-0.0649, -0.0937, 0.0125, 0.0342, -0.0533]],\n",
"\n",
" [[-0.0323, 0.0780, 0.0092, 0.0052, -0.0284],\n",
" [-0.1046, -0.1086, -0.0552, -0.0587, 0.0360],\n",
" [-0.0336, -0.0452, 0.1101, 0.0402, 0.0823],\n",
" [-0.0559, -0.0472, 0.0424, -0.0769, -0.0755],\n",
" [-0.0056, -0.0422, -0.0866, 0.0685, 0.0929]],\n",
"\n",
" [[ 0.0187, -0.0201, -0.1070, -0.0421, 0.0294],\n",
" [ 0.0544, -0.0146, -0.0457, 0.0643, -0.0920],\n",
" [ 0.0730, -0.0448, 0.0018, -0.0228, 0.0140],\n",
" [-0.0349, 0.0840, -0.0030, 0.0901, 0.1110],\n",
" [-0.0563, -0.0842, 0.0926, 0.0905, -0.0882]]],\n",
"\n",
"\n",
" [[[-0.0089, -0.1139, -0.0945, 0.0223, 0.0307],\n",
" [ 0.0245, -0.0314, 0.1065, 0.0165, -0.0681],\n",
" [-0.0065, 0.0277, 0.0404, -0.0816, 0.0433],\n",
" [-0.0590, -0.0959, -0.0631, 0.1114, 0.0987],\n",
" [ 0.1034, 0.0678, 0.0872, -0.0155, -0.0635]],\n",
"\n",
" [[ 0.0577, -0.0598, -0.0779, -0.0369, 0.0242],\n",
" [ 0.0594, -0.0448, -0.0680, 0.0156, -0.0681],\n",
" [-0.0752, 0.0602, -0.0194, 0.1055, 0.1123],\n",
" [ 0.0345, 0.0397, 0.0266, 0.0018, -0.0084],\n",
" [ 0.0016, 0.0431, 0.1074, -0.0299, -0.0488]],\n",
"\n",
" [[-0.0280, -0.0558, 0.0196, 0.0862, 0.0903],\n",
" [ 0.0530, -0.0850, -0.0620, -0.0254, -0.0213],\n",
" [ 0.0095, -0.1060, 0.0359, -0.0881, -0.0731],\n",
" [-0.0960, 0.1006, -0.1093, 0.0871, -0.0039],\n",
" [-0.0134, 0.0722, -0.0107, 0.0724, 0.0835]]],\n",
"\n",
"\n",
" [[[-0.1003, 0.0444, 0.0218, 0.0248, 0.0169],\n",
" [ 0.0316, -0.0555, -0.0148, 0.1097, 0.0776],\n",
" [-0.0043, -0.1086, 0.0051, -0.0786, 0.0939],\n",
" [-0.0701, -0.0083, -0.0256, 0.0205, 0.1087],\n",
" [ 0.0110, 0.0669, 0.0896, 0.0932, -0.0399]],\n",
"\n",
" [[-0.0258, 0.0556, -0.0315, 0.0541, -0.0252],\n",
" [-0.0783, 0.0470, 0.0177, 0.0515, 0.1147],\n",
" [ 0.0788, 0.1095, 0.0062, -0.0993, -0.0810],\n",
" [-0.0717, -0.1018, -0.0579, -0.1063, -0.1065],\n",
" [-0.0690, -0.1138, -0.0709, 0.0440, 0.0963]],\n",
"\n",
" [[-0.0343, -0.0336, 0.0617, -0.0570, -0.0546],\n",
" [ 0.0711, -0.1006, 0.0141, 0.1020, 0.0198],\n",
" [ 0.0314, -0.0672, -0.0016, 0.0063, 0.0283],\n",
" [ 0.0449, 0.1003, -0.0881, 0.0035, -0.0577],\n",
" [-0.0913, -0.0092, -0.1016, 0.0806, 0.0134]]],\n",
"\n",
"\n",
" [[[-0.0622, 0.0603, -0.1093, -0.0447, -0.0225],\n",
" [-0.0981, -0.0734, -0.0188, 0.0876, 0.1115],\n",
" [ 0.0735, -0.0689, -0.0755, 0.1008, 0.0408],\n",
" [ 0.0031, 0.0156, -0.0928, -0.0386, 0.1112],\n",
" [-0.0285, -0.0058, -0.0959, -0.0646, -0.0024]],\n",
"\n",
" [[-0.0717, -0.0143, 0.0470, -0.1130, 0.0343],\n",
" [-0.0763, -0.0564, 0.0443, 0.0918, -0.0316],\n",
" [-0.0474, -0.1044, -0.0595, -0.1011, -0.0264],\n",
" [ 0.0236, -0.1082, 0.1008, 0.0724, -0.1130],\n",
" [-0.0552, 0.0377, -0.0237, -0.0126, -0.0521]],\n",
"\n",
" [[ 0.0927, -0.0645, 0.0958, 0.0075, 0.0232],\n",
" [ 0.0901, -0.0190, -0.0657, -0.0187, 0.0937],\n",
" [-0.0857, 0.0262, -0.1135, 0.0605, 0.0427],\n",
" [ 0.0049, 0.0496, 0.0001, 0.0639, -0.0914],\n",
" [-0.0170, 0.0512, 0.1150, 0.0588, -0.0840]]],\n",
"\n",
"\n",
" [[[ 0.0888, -0.0257, -0.0247, -0.1050, -0.0182],\n",
" [ 0.0817, 0.0161, -0.0673, 0.0355, -0.0370],\n",
" [ 0.1054, -0.1002, -0.0365, -0.1115, -0.0455],\n",
" [ 0.0364, 0.1112, 0.0194, 0.1132, 0.0226],\n",
" [ 0.0667, 0.0926, 0.0965, -0.0646, 0.1062]],\n",
"\n",
" [[ 0.0699, -0.0540, -0.0551, -0.0969, 0.0290],\n",
" [-0.0936, 0.0488, 0.0365, -0.1003, 0.0315],\n",
" [-0.0094, 0.0527, 0.0663, -0.1148, 0.1059],\n",
" [ 0.0968, 0.0459, -0.1055, -0.0412, -0.0335],\n",
" [-0.0297, 0.0651, 0.0420, 0.0915, -0.0432]],\n",
"\n",
" [[ 0.0389, 0.0411, -0.0961, -0.1120, -0.0599],\n",
" [ 0.0790, -0.1087, -0.1005, 0.0647, 0.0623],\n",
" [ 0.0950, -0.0872, -0.0845, 0.0592, 0.1004],\n",
" [ 0.0691, 0.0181, 0.0381, 0.1096, -0.0745],\n",
" [-0.0524, 0.0808, -0.0790, -0.0637, 0.0843]]]])), ('bias', tensor([ 0.0364, 0.0373, -0.0489, -0.0016, 0.1057, -0.0693, 0.0009, 0.0549,\n",
" -0.0797, 0.1121]))])\n"
]
}
],
"source": [
"# Check out the conv_layer_2 internal parameters\n",
"print(conv_layer_2.state_dict())"
]
},
{
"cell_type": "markdown",
"id": "8b708eb6-ae46-4d8c-a8a4-1392827d3e37",
"metadata": {
"id": "8b708eb6-ae46-4d8c-a8a4-1392827d3e37"
},
"source": [
"Look at that! A bunch of random numbers for a weight and bias tensor.\n",
"\n",
"The shapes of these are manipulated by the inputs we passed to `nn.Conv2d()` when we set it up.\n",
"\n",
"Let's check them out."
]
},
{
"cell_type": "code",
"execution_count": 37,
"id": "e5518d61-c0b7-4351-b5ea-4d6b6144291a",
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/"
},
"id": "e5518d61-c0b7-4351-b5ea-4d6b6144291a",
"outputId": "14ef701e-c82d-4fae-9dd6-e18352817cf2"
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"conv_layer_2 weight shape: \n",
"torch.Size([10, 3, 5, 5]) -> [out_channels=10, in_channels=3, kernel_size=5, kernel_size=5]\n",
"\n",
"conv_layer_2 bias shape: \n",
"torch.Size([10]) -> [out_channels=10]\n"
]
}
],
"source": [
"# Get shapes of weight and bias tensors within conv_layer_2\n",
"print(f\"conv_layer_2 weight shape: \\n{conv_layer_2.weight.shape} -> [out_channels=10, in_channels=3, kernel_size=5, kernel_size=5]\")\n",
"print(f\"\\nconv_layer_2 bias shape: \\n{conv_layer_2.bias.shape} -> [out_channels=10]\")"
]
},
{
"cell_type": "markdown",
"id": "f0de23c7-4501-4156-80a4-ac889a636a42",
"metadata": {
"id": "f0de23c7-4501-4156-80a4-ac889a636a42"
},
"source": [
"> **Question:** What should we set the parameters of our `nn.Conv2d()` layers?\n",
">\n",
"> That's a good one. But similar to many other things in machine learning, the values of these aren't set in stone (and recall, because these values are ones we can set ourselves, they're referred to as \"**hyperparameters**\"). \n",
">\n",
"> The best way to find out is to try out different values and see how they effect your model's performance.\n",
">\n",
"> Or even better, find a working example on a problem similar to yours (like we've done with TinyVGG) and copy it. \n",
"\n",
"We're working with a different of layer here to what we've seen before.\n",
"\n",
"But the premise remains the same: start with random numbers and update them to better represent the data."
]
},
{
"cell_type": "markdown",
"id": "6370d45d-ca44-4fa0-a2d7-efaf0a207b91",
"metadata": {
"id": "6370d45d-ca44-4fa0-a2d7-efaf0a207b91"
},
"source": [
"### 7.2 Stepping through `nn.MaxPool2d()`\n",
"Now let's check out what happens when we move data through `nn.MaxPool2d()`."
]
},
{
"cell_type": "code",
"execution_count": 38,
"id": "1164c753-19d9-43b7-a04f-017d0f7188c3",
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/"
},
"id": "1164c753-19d9-43b7-a04f-017d0f7188c3",
"outputId": "9c46f08e-928d-4ee4-e43c-b402113fc2b4"
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Test image original shape: torch.Size([3, 64, 64])\n",
"Test image with unsqueezed dimension: torch.Size([1, 3, 64, 64])\n",
"Shape after going through conv_layer(): torch.Size([1, 10, 62, 62])\n",
"Shape after going through conv_layer() and max_pool_layer(): torch.Size([1, 10, 31, 31])\n"
]
}
],
"source": [
"# Print out original image shape without and with unsqueezed dimension\n",
"print(f\"Test image original shape: {test_image.shape}\")\n",
"print(f\"Test image with unsqueezed dimension: {test_image.unsqueeze(dim=0).shape}\")\n",
"\n",
"# Create a sample nn.MaxPoo2d() layer\n",
"max_pool_layer = nn.MaxPool2d(kernel_size=2)\n",
"\n",
"# Pass data through just the conv_layer\n",
"test_image_through_conv = conv_layer(test_image.unsqueeze(dim=0))\n",
"print(f\"Shape after going through conv_layer(): {test_image_through_conv.shape}\")\n",
"\n",
"# Pass data through the max pool layer\n",
"test_image_through_conv_and_max_pool = max_pool_layer(test_image_through_conv)\n",
"print(f\"Shape after going through conv_layer() and max_pool_layer(): {test_image_through_conv_and_max_pool.shape}\")"
]
},
{
"cell_type": "markdown",
"id": "de029abd-6674-4bfa-99ab-322f339f89f4",
"metadata": {
"id": "de029abd-6674-4bfa-99ab-322f339f89f4"
},
"source": [
"Notice the change in the shapes of what's happening in and out of a `nn.MaxPool2d()` layer.\n",
"\n",
"The `kernel_size` of the `nn.MaxPool2d()` layer will effects the size of the output shape.\n",
"\n",
"In our case, the shape halves from a `62x62` image to `31x31` image.\n",
"\n",
"Let's see this work with a smaller tensor."
]
},
{
"cell_type": "code",
"execution_count": 39,
"id": "e6a2b196-4845-4b40-9212-e75406e88875",
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/"
},
"id": "e6a2b196-4845-4b40-9212-e75406e88875",
"outputId": "5a5e5df1-8e25-4061-d223-398ecfc7ef4c"
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Random tensor:\n",
"tensor([[[[0.3367, 0.1288],\n",
" [0.2345, 0.2303]]]])\n",
"Random tensor shape: torch.Size([1, 1, 2, 2])\n",
"\n",
"Max pool tensor:\n",
"tensor([[[[0.3367]]]]) <- this is the maximum value from random_tensor\n",
"Max pool tensor shape: torch.Size([1, 1, 1, 1])\n"
]
}
],
"source": [
"torch.manual_seed(42)\n",
"# Create a random tensor with a similiar number of dimensions to our images\n",
"random_tensor = torch.randn(size=(1, 1, 2, 2))\n",
"print(f\"Random tensor:\\n{random_tensor}\")\n",
"print(f\"Random tensor shape: {random_tensor.shape}\")\n",
"\n",
"# Create a max pool layer\n",
"max_pool_layer = nn.MaxPool2d(kernel_size=2) # see what happens when you change the kernel_size value \n",
"\n",
"# Pass the random tensor through the max pool layer\n",
"max_pool_tensor = max_pool_layer(random_tensor)\n",
"print(f\"\\nMax pool tensor:\\n{max_pool_tensor} <- this is the maximum value from random_tensor\")\n",
"print(f\"Max pool tensor shape: {max_pool_tensor.shape}\")"
]
},
{
"cell_type": "markdown",
"id": "002e586e-dcb3-40fe-a7dd-a1c18a3b8da0",
"metadata": {
"id": "002e586e-dcb3-40fe-a7dd-a1c18a3b8da0"
},
"source": [
"Notice the final two dimensions between `random_tensor` and `max_pool_tensor`, they go from `[2, 2]` to `[1, 1]`.\n",
"\n",
"In essence, they get halved.\n",
"\n",
"And the change would be different for different values of `kernel_size` for `nn.MaxPool2d()`.\n",
"\n",
"Also notice the value leftover in `max_pool_tensor` is the **maximum** value from `random_tensor`.\n",
"\n",
"What's happening here?\n",
"\n",
"This is another important piece of the puzzle of neural networks.\n",
"\n",
"Essentially, **every layer in a neural network is trying to compress data from higher dimensional space to lower dimensional space**. \n",
"\n",
"In other words, take a lot of numbers (raw data) and learn patterns in those numbers, patterns that are predictive whilst also being *smaller* in size than the original values.\n",
"\n",
"From an artificial intelligence perspective, you could consider the whole goal of a neural network to *compress* information.\n",
"\n",
"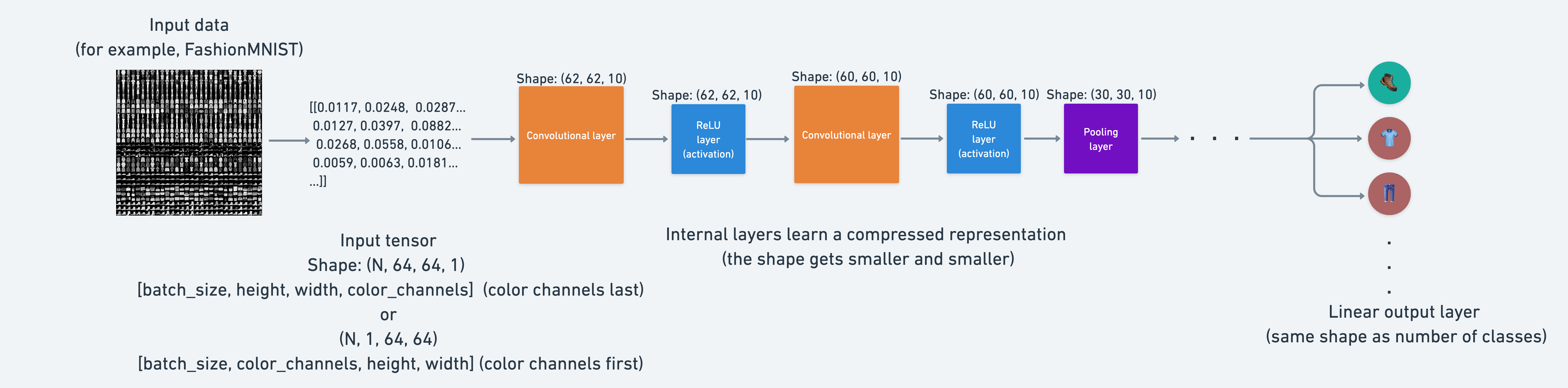\n",
"\n",
"This means, that from the point of view of a neural network, intelligence is compression.\n",
"\n",
"This is the idea of the use of a `nn.MaxPool2d()` layer: take the maximum value from a portion of a tensor and disregard the rest.\n",
"\n",
"In essence, lowering the dimensionality of a tensor whilst still retaining a (hopefully) significant portion of the information.\n",
"\n",
"It is the same story for a `nn.Conv2d()` layer.\n",
"\n",
"Except instead of just taking the maximum, the `nn.Conv2d()` performs a convolutional operation on the data (see this in action on the [CNN Explainer webpage](https://poloclub.github.io/cnn-explainer/)).\n",
"\n",
"> **Exercise:** What do you think the [`nn.AvgPool2d()`](https://pytorch.org/docs/stable/generated/torch.nn.AvgPool2d.html) layer does? Try making a random tensor like we did above and passing it through. Check the input and output shapes as well as the input and output values.\n",
"\n",
"> **Extra-curriculum:** Lookup \"most common convolutional neural networks\", what architectures do you find? Are any of them contained within the [`torchvision.models`](https://pytorch.org/vision/stable/models.html) library? What do you think you could do with these?"
]
},
{
"cell_type": "markdown",
"id": "39a3c646-52f0-4f4b-8527-2fc33d0dfb13",
"metadata": {
"id": "39a3c646-52f0-4f4b-8527-2fc33d0dfb13"
},
"source": [
"### 7.3 Setup a loss function and optimizer for `model_2`\n",
"\n",
"We've stepped through the layers in our first CNN enough.\n",
"\n",
"But remember, if something still isn't clear, try starting small.\n",
"\n",
"Pick a single layer of a model, pass some data through it and see what happens.\n",
"\n",
"Now it's time to move forward and get to training!\n",
"\n",
"Let's setup a loss function and an optimizer.\n",
"\n",
"We'll use the functions as before, `nn.CrossEntropyLoss()` as the loss function (since we're working with multi-class classification data).\n",
"\n",
"And `torch.optim.SGD()` as the optimizer to optimize `model_2.parameters()` with a learning rate of `0.1`."
]
},
{
"cell_type": "code",
"execution_count": 40,
"id": "06a76a1b-5f6f-4018-bf7b-8388b385476f",
"metadata": {
"id": "06a76a1b-5f6f-4018-bf7b-8388b385476f"
},
"outputs": [],
"source": [
"# Setup loss and optimizer\n",
"loss_fn = nn.CrossEntropyLoss()\n",
"optimizer = torch.optim.SGD(params=model_2.parameters(), \n",
" lr=0.1)"
]
},
{
"cell_type": "markdown",
"id": "758bc223-a244-4604-a07a-e2fc2f96c2f6",
"metadata": {
"id": "758bc223-a244-4604-a07a-e2fc2f96c2f6"
},
"source": [
"### 7.4 Training and testing `model_2` using our training and test functions\n",
"\n",
"Loss and optimizer ready!\n",
"\n",
"Time to train and test.\n",
"\n",
"We'll use our `train_step()` and `test_step()` functions we created before.\n",
"\n",
"We'll also measure the time to compare it to our other models."
]
},
{
"cell_type": "code",
"execution_count": 41,
"id": "861d126e-d876-40b3-9b7a-66cfc2f1bf05",
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/",
"height": 327,
"referenced_widgets": [
"2b9c90ceb8554eaaaaf33acacecbcc11",
"9051de473b1b456592576115260f0c48",
"a315b7b535e4461ca11a6d96ca74411c",
"4cd01ed6c2534d4e80a0af2e9da02052",
"eb3ca30526e24fff9194d4e82436df99",
"6117713ba6c9490fab837cfbad7d442b",
"d426a4e9fff447ea95c7256372e272b7",
"fdcf4db7208d42b5acb35bf56c72fd82",
"606df8221adf48308f48c86ac54475e8",
"ebc6218d07f54005b0e46553b83464e1",
"03435ac81db84ae6bb6cb99bb78167c2"
]
},
"id": "861d126e-d876-40b3-9b7a-66cfc2f1bf05",
"outputId": "77ae1601-bf72-4239-b3f6-9fb99a1c62c0"
},
"outputs": [
{
"data": {
"application/vnd.jupyter.widget-view+json": {
"model_id": "2b9c90ceb8554eaaaaf33acacecbcc11",
"version_major": 2,
"version_minor": 0
},
"text/plain": [
" 0%| | 0/3 [00:00\n",
"
\n",
" "
],
"text/plain": [
" model_name model_loss model_acc training_time\n",
"0 FashionMNISTModelV0 0.476639 83.426518 32.348722\n",
"1 FashionMNISTModelV1 0.685001 75.019968 36.877976\n",
"2 FashionMNISTModelV2 0.328570 88.378594 44.249765"
]
},
"execution_count": 44,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Add training times to results comparison\n",
"compare_results[\"training_time\"] = [total_train_time_model_0,\n",
" total_train_time_model_1,\n",
" total_train_time_model_2]\n",
"compare_results"
]
},
{
"cell_type": "markdown",
"id": "fbbe5832-1081-4c76-8d5b-06c7a06da7b9",
"metadata": {
"id": "fbbe5832-1081-4c76-8d5b-06c7a06da7b9"
},
"source": [
"It looks like our CNN (`FashionMNISTModelV2`) model performed the best (lowest loss, highest accuracy) but had the longest training time.\n",
"\n",
"And our baseline model (`FashionMNISTModelV0`) performed better than `model_1` (`FashionMNISTModelV1`).\n",
"\n",
"### Performance-speed tradeoff\n",
"\n",
"Something to be aware of in machine learning is the **performance-speed** tradeoff.\n",
"\n",
"Generally, you get better performance out of a larger, more complex model (like we did with `model_2`).\n",
"\n",
"However, this performance increase often comes at a sacrifice of training speed and inference speed.\n",
"\n",
"> **Note:** The training times you get will be very dependant on the hardware you use. \n",
">\n",
"> Generally, the more CPU cores you have, the faster your models will train on CPU. And similar for GPUs.\n",
"> \n",
"> Newer hardware (in terms of age) will also often train models faster due to incorporating technology advances.\n",
"\n",
"How about we get visual?"
]
},
{
"cell_type": "code",
"execution_count": 45,
"id": "5eb0df60-9318-47d0-adce-f8788ed3999e",
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/",
"height": 449
},
"id": "5eb0df60-9318-47d0-adce-f8788ed3999e",
"outputId": "d904e039-1544-49f5-bed7-b17555d03b5a"
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAr0AAAGwCAYAAACkUt2bAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/bCgiHAAAACXBIWXMAAA9hAAAPYQGoP6dpAAA9IklEQVR4nO3de1wWZd7H8S/KQQ6iIB5CQQkkRUFwzVRKH9RdZAnbLEtTsIDdLMxYz50WTQ1IqTyUbB7AntXUAjuYq2uaFqilGIrJqnkuj6sGHhFhnj96vLc7UBE1dPy8X695xT1zzTW/ueaVfu/xmsHGMAxDAAAAgInVqukCAAAAgJuN0AsAAADTI/QCAADA9Ai9AAAAMD1CLwAAAEyP0AsAAADTI/QCAADA9GxrugDgVlBeXq6DBw+qbt26srGxqelyAABAFRiGoVOnTsnT01O1al35Xi6hF5B08OBBeXl51XQZAACgGg4cOKBmzZpdsQ2hF5BUt25dST//T+Pq6lrD1QAAgKooLi6Wl5eX5e/xKyH0ApJlSoOrqyuhFwCA20xVpibyIBsAAABMj9ALAAAA0yP0AgAAwPQIvQAAADA9Qi8AAABMj9ALAAAA0yP0AgAAwPQIvQAAADA9Qi8AAABMj9ALAAAA0yP0AgAAwPQIvQAAADA9Qi8AAABMj9ALAAAA0yP0AgAAwPQIvQAAADA9Qi8AAABMj9ALAAAA0yP0AgAAwPQIvQAAADA9Qi8AAABMj9ALAAAA0yP0AgAAwPQIvQAAADA9Qi8AAABMj9ALAAAA0yP0AgAAwPQIvQAAADA925ouALiVtE1arloOTjVdBgAAprI3JbKmS+BOLwAAAMyP0AsAAADTI/QCAADA9Ai9AAAAMD1CLwAAAEyP0AsAAADTI/QCAADA9Ai9AAAAMD1CLwAAAEyP0AsAAADTI/QCAADA9Ai9AAAAMD1CLwAAAEyP0AsAAADTI/QCAADA9Ai9AAAAMD1CLwAAAEyP0AsAAADTI/QCAADA9Ai9AAAAMD1CLwAAAEyP0AsAAADTI/QCAADA9Ai9AAAAMD1CLwAAAEzPdKF39erVsrGx0U8//XTZNmPHjlVwcPBvVtOdqirX4tdatGiht95666bVBAAA7kw1GnqffPJJ2djYVFi+//77m3rcESNGaOXKlTe0z0sBz83NTefPn7fatmHDBsu5/bp9mzZtVFZWZtW+fv36yszMtHz+dRDcvHmzevfurUaNGqlOnTpq0aKFHn/8cR09elRjx46tdEx/uUj/HfvBgwdXOJeEhATZ2NjoySefvP6BqaYLFy7Iw8NDKSkplW4fP368GjdurNLSUmVnZ+v3v/+9GjZsKFdXV3Xu3FnLly//jSsGAAC3shq/09urVy8dOnTIavHx8bmpx3RxcVGDBg1uSt9169bV4sWLrdbNnj1b3t7elbbfvXu33nvvvSr3f+zYMfXo0UPu7u5avny5CgsLlZGRIU9PT505c0YjRoywGstmzZrp1VdftVp3iZeXlxYsWKBz585Z1p0/f17z58+/bL2/FXt7ew0cOFAZGRkVthmGoczMTMXExMjOzk5ffvmlfv/732vp0qXKy8tTWFiYoqKi9O2339ZA5QAA4FZU46HXwcFBTZo0sVqmTJmiwMBAOTs7y8vLS88++6xOnz5t2Wffvn2KioqSm5ubnJ2d1aZNGy1dutSq37y8PHXo0EFOTk7q0qWLtm/fbtn26+kN5eXlevXVV9WsWTM5ODgoODhYy5Yts2zfu3evbGxslJ2drbCwMDk5Oaldu3Zat25dhfMZNGiQ5syZY/l87tw5LViwQIMGDar0/J977jklJSWppKSkSuOVm5uroqIizZo1SyEhIfLx8VFYWJjefPNN+fj4yMXFxWosa9eurbp161qtu6R9+/by8vJSdna2ZV12dra8vb0VEhJiddySkhINHTrUcnf5/vvv14YNG6zaLF26VP7+/nJ0dFRYWJj27t1bof6cnBw98MADcnR0lJeXl4YOHaozZ85Ueq5xcXHasWOHcnJyrNavWbNGu3fvVlxcnCTprbfe0qhRo3TvvfeqZcuWeu2119SyZUt9+umnVRpTAABgfjUeeitTq1YtTZ06Vd99953mzp2rVatWadSoUZbtCQkJKikp0ZdffqmCggKlpqbKxcXFqo+XXnpJaWlp2rhxo2xtbRUbG3vZ402ZMkVpaWmaPHmytmzZovDwcPXu3Vs7d+6s0OeIESOUn58vf39/9e/fXxcvXrRqEx0dra+++kr79++XJGVlZalFixZq3759pcdOTEzUxYsXNW3atCqNTZMmTXTx4kUtXrxYhmFUaZ8riY2NtbqbOmfOHD311FMV2o0aNUpZWVmaO3euNm3aJD8/P4WHh+vEiROSpAMHDqhPnz6KiopSfn6+4uPjNWbMGKs+du3apV69eumRRx7Rli1btHDhQuXk5GjIkCGV1hYYGKh7773X6kuEJGVkZKhLly5q1apVpfuVl5fr1KlTcnd3v+x5l5SUqLi42GoBAADmVeOhd8mSJXJxcbEsffv2VWJiosLCwtSiRQt1795dEyZM0KJFiyz77N+/X6GhoQoMDNTdd9+tBx98UF27drXqd+LEierWrZsCAgI0ZswYrV27tsJc20smT56s0aNHq1+/frrnnnuUmpqq4ODgCg9UjRgxQpGRkfL399e4ceO0b9++CvOPGzVqpIiICMuc3Dlz5lwxcDs5OSkpKUnJyckqKiq66nh16tRJL774op544gl5eHgoIiJCkyZN0pEjR666b2UGDhyonJwc7du3T/v27VNubq4GDhxo1ebMmTOaMWOGJk2apIiICAUEBGjmzJlydHTU7NmzJUkzZsyQr6+v0tLSdM8992jAgAEV5gQnJydrwIABSkxMVMuWLdWlSxdNnTpV77333mWvTVxcnD744APLnf5Tp07pww8/vOKYTp48WadPn9Zjjz122TbJycmqV6+eZfHy8qrKcAEAgNtUjYfesLAw5efnW5apU6fq888/V48ePdS0aVPVrVtX0dHROn78uM6ePStJGjp0qCZMmKDQ0FAlJSVpy5YtFfoNCgqy/HzXXXdJko4ePVqhXXFxsQ4ePKjQ0FCr9aGhoSosLKxWn7GxscrMzNTu3bu1bt06DRgw4IpjEBcXpwYNGig1NfWK7S6ZOHGiDh8+rPT0dLVp00bp6elq1aqVCgoKqrT/LzVs2FCRkZHKzMxURkaGIiMj5eHhYdVm165dKi0ttRojOzs7dezY0TJGhYWFuu+++6z269y5s9XnzZs3KzMz0+pLTnh4uMrLy7Vnz55K6+vfv7/KysosX3oWLlyoWrVq6fHHH6+0/fz58zVu3DgtWrRIjRo1uux5v/DCCyoqKrIsBw4cuGxbAABw+6vx0Ovs7Cw/Pz/LUlJSogcffFBBQUHKyspSXl6e3n77bUk/P9EvSfHx8dq9e7eio6NVUFCgDh06VJgeYGdnZ/n50hsLysvLr6vWqvYZERGhc+fOKS4uTlFRUVd9aM7W1lYTJ07UlClTdPDgwSrV0qBBA/Xt21eTJ09WYWGhPD09NXny5Gs4m/+6FNLnzp17xTuo1+v06dN6+umnrb7kbN68WTt37pSvr2+l+7i6uurRRx+1TMHIyMjQY489VmE6iyQtWLBA8fHxWrRokXr27HnFWhwcHOTq6mq1AAAA86rx0PtreXl5Ki8vV1pamjp16iR/f/9Kg6CXl5cGDx6s7OxsDR8+XDNnzqzW8VxdXeXp6anc3Fyr9bm5uQoICKhWn7a2toqJidHq1aurHCL79u2rNm3aaNy4cdd8PHt7e/n6+l72gbCr6dWrly5cuKDS0lKFh4dX2O7r6yt7e3urMSotLdWGDRssY9S6dWt98803VvutX7/e6nP79u21bds2qy85lxZ7e/vL1hcXF6ecnBwtWbJEa9eutTzA9kvvv/++nnrqKb3//vuKjIy8pvMHAADmZ1vTBfyan5+fSktLNW3aNEVFRSk3N1fp6elWbRITExURESF/f3+dPHlSX3zxhVq3bl3tY44cOVJJSUny9fVVcHCwMjIylJ+fr3nz5lW7z/Hjx2vkyJHX9Gq0lJSUSkPnLy1ZskQLFixQv3795O/vL8Mw9Omnn2rp0qWVvt6rKmrXrm2ZplC7du0K252dnfXMM89o5MiRcnd3l7e3t15//XWdPXvWEkAHDx6stLQ0jRw5UvHx8crLy7N617AkjR49Wp06ddKQIUMUHx8vZ2dnbdu2TStWrND06dMvW1/Xrl3l5+enmJgYtWrVSl26dLHaPn/+fA0aNEhTpkzRfffdp8OHD0uSHB0dVa9evWqNCQAAMJdb7k5vu3bt9MYbbyg1NVVt27bVvHnzlJycbNWmrKxMCQkJat26tXr16iV/f3+988471T7m0KFDNWzYMA0fPlyBgYFatmyZPvnkE7Vs2bLafdrb28vDw8PqF1JcTffu3dW9e/cKb4T4pYCAADk5OWn48OEKDg5Wp06dtGjRIs2aNUvR0dHVrvdq/8SfkpKiRx55RNHR0Wrfvr2+//57LV++XG5ubpIkb29vZWVl6aOPPlK7du2Unp6u1157zaqPoKAgrVmzRjt27NADDzygkJAQ/e1vf5Onp+cVa7OxsVFsbKxOnjxZ6Z3zd999VxcvXlRCQoLuuusuy/L8889XYyQAAIAZ2Rg34r1XwG2uuLj457c4JC5SLQenmi4HAABT2Ztyc6YeXvr7u6io6KrP59xyd3oBAACAG43QCwAAANMj9AIAAMD0CL0AAAAwPUIvAAAATI/QCwAAANMj9AIAAMD0CL0AAAAwPUIvAAAATI/QCwAAANMj9AIAAMD0CL0AAAAwPUIvAAAATI/QCwAAANMj9AIAAMD0CL0AAAAwPUIvAAAATI/QCwAAANMj9AIAAMD0CL0AAAAwPUIvAAAATI/QCwAAANMj9AIAAMD0CL0AAAAwPduaLgC4lWwdFy5XV9eaLgMAANxg3OkFAACA6RF6AQAAYHqEXgAAAJgeoRcAAACmR+gFAACA6RF6AQAAYHqEXgAAAJgeoRcAAACmR+gFAACA6RF6AQAAYHqEXgAAAJgeoRcAAACmR+gFAACA6RF6AQAAYHqEXgAAAJgeoRcAAACmR+gFAACA6RF6AQAAYHqEXgAAAJgeoRcAAACmR+gFAACA6RF6AQAAYHqEXgAAAJgeoRcAAACmR+gFAACA6RF6AQAAYHqEXgAAAJgeoRcAAACmR+gFAACA6RF6AQAAYHqEXgAAAJgeoRcAAACmR+gFAACA6RF6AQAAYHqEXgAAAJgeoRcAAACmR+gFAACA6RF6AQAAYHqEXgAAAJgeoRcAAACmR+gFAACA6RF6AQAAYHqEXgAAAJgeoRcAAACmR+gFAACA6RF6AQAAYHqEXgAAAJgeoRcAAACmR+gFAACA6RF6AQAAYHqEXgAAAJgeoRcAAACmR+gFAACA6RF6AQAAYHqEXgAAAJgeoRcAAACmR+gFAACA6RF6AQAAYHqEXgAAAJgeoRcAAACmZ1vTBQC3krZJy1XLwammywAA3Gb2pkTWdAm4Cu70AgAAwPQIvQAAADA9Qi8AAABMj9ALAAAA0yP0AgAAwPQIvQAAADA9Qi8AAABMj9ALAAAA0yP0AgAAwPQIvQAAADA9Qi8AAABMj9ALAAAA0yP0AgAAwPRsq9rQzc1NNjY2VWp74sSJahcEAAAA3GhVDr1vvfXWTSwDAAAAuHmqHHoHDRp0M+sAAAAAbppqz+ndtWuXXn75ZfXv319Hjx6VJP3zn//Ud999d8OKAwAAAG6EaoXeNWvWKDAwUF9//bWys7N1+vRpSdLmzZuVlJR0QwsEAAAArle1Qu+YMWM0YcIErVixQvb29pb13bt31/r1629YcQAAAMCNUK3QW1BQoIcffrjC+kaNGuk///nPdRcFAAAA3EjVCr3169fXoUOHKqz/9ttv1bRp0+suCgAAALiRqhV6+/Xrp9GjR+vw4cOysbFReXm5cnNzNWLECMXExNzoGgEAAIDrUq3Q+9prr6lVq1by8vLS6dOnFRAQoK5du6pLly56+eWXb3SNAAAAwHWp8nt6f8ne3l4zZ87UK6+8oq1bt+r06dMKCQlRy5Ytb3R9AAAAwHWrVui9xNvbW97e3jeqFgAAAOCmqHLoHTZsWJU7feONN6pVzI2wevVqhYWF6eTJk6pfv36lbcaOHauPPvpI+fn5v2ltd5qqXItfa9GihRITE5WYmHhTawMAAHeWKs/p/fbbb62W2bNn6+9//7tWr16t1atX691339Xs2bOvKUg++eSTsrGxqbB8//331TmXKhsxYoRWrlx5Q/tcvXq1bGxs5ObmpvPnz1tt27Bhg+Xcft2+TZs2Kisrs2pfv359ZWZmWj63aNFCb731luXz5s2b1bt3bzVq1Eh16tRRixYt9Pjjj+vo0aMaO3ZspWP6y0X679gPHjy4wrkkJCTIxsZGTz755PUPTDVduHBBHh4eSklJqXT7+PHj1bhxY5WWlurQoUN64okn5O/vr1q1ahGYAQBABVUOvV988YVliYqKUrdu3fTDDz9o06ZN2rRpkw4cOKCwsDBFRkZeUwG9evXSoUOHrBYfH59rPpFr4eLiogYNGtyUvuvWravFixdbrZs9e/Zlp4Hs3r1b7733XpX7P3bsmHr06CF3d3ctX75chYWFysjIkKenp86cOaMRI0ZYjWWzZs306quvWq27xMvLSwsWLNC5c+cs686fP6/58+fX+LQVe3t7DRw4UBkZGRW2GYahzMxMxcTEyM7OTiUlJWrYsKFefvlltWvXrgaqBQAAt7pqvb0hLS1NycnJcnNzs6xzc3PThAkTlJaWdk19OTg4qEmTJlbLlClTFBgYKGdnZ3l5eenZZ5+1/KpjSdq3b5+ioqLk5uYmZ2dntWnTRkuXLrXqNy8vTx06dJCTk5O6dOmi7du3W7aNHTtWwcHBls/l5eV69dVX1axZMzk4OCg4OFjLli2zbN+7d69sbGyUnZ2tsLAwOTk5qV27dlq3bl2F8xk0aJDmzJlj+Xzu3DktWLBAgwYNqvT8n3vuOSUlJamkpKRK45Wbm6uioiLNmjVLISEh8vHxUVhYmN588035+PjIxcXFaixr166tunXrWq27pH379vLy8lJ2drZlXXZ2try9vRUSEmJ13JKSEg0dOtRyd/n+++/Xhg0brNosXbpU/v7+cnR0VFhYmPbu3Vuh/pycHD3wwANydHSUl5eXhg4dqjNnzlR6rnFxcdqxY4dycnKs1q9Zs0a7d+9WXFycpJ/vhE+ZMkUxMTGqV69elcYRAADcWaoVeouLi3Xs2LEK648dO6ZTp05df1G1amnq1Kn67rvvNHfuXK1atUqjRo2ybE9ISFBJSYm+/PJLFRQUKDU1VS4uLlZ9vPTSS0pLS9PGjRtla2ur2NjYyx5vypQpSktL0+TJk7VlyxaFh4erd+/e2rlzZ4U+R4wYofz8fPn7+6t///66ePGiVZvo6Gh99dVX2r9/vyQpKytLLVq0UPv27Ss9dmJioi5evKhp06ZVaWyaNGmiixcvavHixTIMo0r7XElsbKzV3dQ5c+boqaeeqtBu1KhRysrK0ty5c7Vp0yb5+fkpPDxcJ06ckCQdOHBAffr0UVRUlPLz8xUfH68xY8ZY9bFr1y716tVLjzzyiLZs2aKFCxcqJydHQ4YMqbS2wMBA3XvvvVZfIiQpIyNDXbp0UatWrap93iUlJSouLrZaAACAeVUr9D788MN66qmnlJ2drR9++EE//PCDsrKyFBcXpz59+lxTX0uWLJGLi4tl6du3rxITExUWFqYWLVqoe/fumjBhghYtWmTZZ//+/QoNDVVgYKDuvvtuPfjgg+ratatVvxMnTlS3bt0UEBCgMWPGaO3atRXm2l4yefJkjR49Wv369dM999yj1NRUBQcHW82jlX6eCxwZGSl/f3+NGzdO+/btqzD/uFGjRoqIiLDMyZ0zZ84VA7eTk5OSkpKUnJysoqKiq45Xp06d9OKLL+qJJ56Qh4eHIiIiNGnSJB05cuSq+1Zm4MCBysnJ0b59+7Rv3z7l5uZq4MCBVm3OnDmjGTNmaNKkSYqIiFBAQIBmzpwpR0dHzZ49W5I0Y8YM+fr6Ki0tTffcc48GDBhQYU5wcnKyBgwYoMTERLVs2VJdunTR1KlT9d5771322sTFxemDDz6w3Ok/deqUPvzwwyuOaVUkJyerXr16lsXLy+u6+gMAALe2aoXe9PR0RURE6IknnlDz5s3VvHlzPfHEE+rVq5feeeeda+orLCxM+fn5lmXq1Kn6/PPP1aNHDzVt2lR169ZVdHS0jh8/rrNnz0qShg4dqgkTJig0NFRJSUnasmVLhX6DgoIsP991112SpKNHj1ZoV1xcrIMHDyo0NNRqfWhoqAoLC6vVZ2xsrDIzM7V7926tW7dOAwYMuOIYxMXFqUGDBkpNTb1iu0smTpyow4cPKz09XW3atFF6erpatWqlgoKCKu3/Sw0bNlRkZKQyMzOVkZGhyMhIeXh4WLXZtWuXSktLrcbIzs5OHTt2tIxRYWGh7rvvPqv9OnfubPV58+bNyszMtPqSEx4ervLycu3Zs6fS+vr376+ysjLLl56FCxeqVq1aevzxx6/5XH/phRdeUFFRkWU5cODAdfUHAABubdUKvU5OTnrnnXd0/Phxy9scTpw4oXfeeUfOzs7X1Jezs7P8/PwsS0lJiR588EEFBQUpKytLeXl5evvttyX9/ES/JMXHx2v37t2Kjo5WQUGBOnToUGF6gJ2dneXnS28sKC8vr87pXnOfEREROnfunOLi4hQVFXXVh+ZsbW01ceJETZkyRQcPHqxSLQ0aNFDfvn01efJkFRYWytPTU5MnT76Gs/mvSyF97ty5130H9UpOnz6tp59+2upLzubNm7Vz5075+vpWuo+rq6seffRRyxSMjIwMPfbYYxWms1wrBwcHubq6Wi0AAMC8qhV6L3F2dpa7u7vc3d2vOexeTl5ensrLy5WWlqZOnTrJ39+/0iDo5eWlwYMHKzs7W8OHD9fMmTOrdTxXV1d5enoqNzfXan1ubq4CAgKq1aetra1iYmK0evXqKofIvn37qk2bNho3btw1H8/e3l6+vr6XfSDsanr16qULFy6otLRU4eHhFbb7+vrK3t7eaoxKS0u1YcMGyxi1bt1a33zzjdV+69evt/rcvn17bdu2zepLzqXF3t7+svXFxcUpJydHS5Ys0dq1ay0PsAEAAFRVtULvpbcd1KtXzzK9oX79+ho/fvx130318/NTaWmppk2bpt27d+t///d/lZ6ebtUmMTFRy5cv1549e7Rp0yZ98cUXat26dbWPOXLkSKWmpmrhwoXavn27xowZo/z8fD3//PPV7nP8+PE6duxYpSHyclJSUjRnzpwrhtclS5Zo4MCBWrJkiXbs2KHt27dr8uTJWrp0qR566KFq1Vq7dm0VFhZq27Ztql27doXtzs7OeuaZZzRy5EgtW7ZM27Zt05///GedPXvWEkAHDx6snTt3auTIkdq+fbvmz59v9a5hSRo9erTWrl2rIUOGKD8/Xzt37tTHH3982QfZLunatav8/PwUExOjVq1aqUuXLhXaXLpzfPr0aR07dkz5+fnatm1btcYDAACYT7V+DfFLL72k2bNnKyUlxTLPMycnR2PHjtX58+c1ceLEahfUrl07vfHGG0pNTdULL7ygrl27Kjk5WTExMZY2ZWVlSkhI0A8//CBXV1f16tVLb775ZrWPOXToUBUVFWn48OE6evSoAgIC9Mknn6hly5bV7tPe3r7C3Nir6d69u7p3765//etfl20TEBAgJycnDR8+XAcOHJCDg4NatmypWbNmKTo6utr1Xu2f91NSUlReXq7o6GidOnVKHTp00PLlyy2vrfP29lZWVpb++te/atq0aerYsaNee+01qzvdQUFBWrNmjV566SU98MADMgxDvr6+V52fa2Njo9jYWL344ot64YUXKm3zy1es5eXlaf78+WrevHmlr00DAAB3HhujGu+98vT0VHp6unr37m21/uOPP9azzz6rH3/88YYVCPwWiouLf36LQ+Ii1XJwqulyAAC3mb0p1/bLuXBjXPr7u6io6Ko38Ko1veHEiROVviO1VatWlve2AgAAALeKaoXedu3aafr06RXWT58+nV8DCwAAgFtOteb0vv7664qMjNTnn39ueRfrunXrtH//fv3zn/+8oQUCAAAA16tad3q7deum7du3q0+fPvrpp5/0008/qU+fPtqxY4ceeOCBG10jAAAAcF2qdadX+vmXI/Tu3VudOnWyvKZs48aNklThATcAAACgJlUr9C5btkwxMTE6fvy4fv3yBxsbG5WVld2Q4gAAAIAboVrTG5577jn17dtXBw8eVHl5udVC4AUAAMCtplqh98iRIxo2bJgaN258o+sBAAAAbrhqhd5HH31Uq1evvsGlAAAAADdHteb0Tp8+XX379tVXX32lwMBA2dnZWW0fOnToDSkOAAAAuBGqFXrff/99/etf/1KdOnW0evVq2djYWLbZ2NgQegEAAHBLqVbofemllzRu3DiNGTNGtWpVa4YEAAAA8JupVmK9cOGCHn/8cQIvAAAAbgvVSq2DBg3SwoULb3QtAAAAwE1RrekNZWVlev3117V8+XIFBQVVeJDtjTfeuCHFAQAAADdCtUJvQUGBQkJCJElbt2612vbLh9oAAACAW0G1Qu8XX3xxo+sAAAAAbhqeRAMAAIDpEXoBAABgeoReAAAAmB6hFwAAAKZH6AUAAIDpEXoBAABgeoReAAAAmF613tMLmNXWceFydXWt6TIAAMANxp1eAAAAmB6hFwAAAKZH6AUAAIDpEXoBAABgeoReAAAAmB6hFwAAAKZH6AUAAIDpEXoBAABgeoReAAAAmB6hFwAAAKZH6AUAAIDpEXoBAABgeoReAAAAmB6hFwAAAKZH6AUAAIDpEXoBAABgeoReAAAAmB6hFwAAAKZH6AUAAIDpEXoBAABgeoReAAAAmB6hFwAAAKZH6AUAAIDpEXoBAABgeoReAAAAmB6hFwAAAKZH6AUAAIDpEXoBAABgeoReAAAAmB6hFwAAAKZH6AUAAIDpEXoBAABgeoReAAAAmB6hFwAAAKZH6AUAAIDpEXoBAABgeoReAAAAmB6hFwAAAKZH6AUAAIDpEXoBAABgeoReAAAAmB6hFwAAAKZH6AUAAIDpEXoBAABgeoReAAAAmB6hFwAAAKZH6AUAAIDpEXoBAABgeoReAAAAmB6hFwAAAKZH6AUAAIDpEXoBAABgeoReAAAAmB6hFwAAAKZH6AUAAIDpEXoBAABgeoReAAAAmB6hFwAAAKZH6AUAAIDpEXoBAABgerY1XQBwK2mbtFy1HJxqugwAAG66vSmRNV3Cb4o7vQAAADA9Qi8AAABMj9ALAAAA0yP0AgAAwPQIvQAAADA9Qi8AAABMj9ALAAAA0yP0AgAAwPQIvQAAADA9Qi8AAABMj9ALAAAA0yP0AgAAwPQIvQAAADA9Qi8AAABMj9ALAAAA0yP0AgAAwPQIvQAAADA9Qi8AAABMj9ALAAAA0yP0AgAAwPQIvQAAADA9Qi8AAABMj9ALAAAA0yP0AgAAwPQIvQAAADA9Qi8AAABMz3Shd/Xq1bKxsdFPP/102TZjx45VcHDwb1bTnaoq1+LXWrRoobfeeuum1QQAAO5MNRp6n3zySdnY2FRYvv/++5t63BEjRmjlypU3tM9LAc/NzU3nz5+32rZhwwbLuf26fZs2bVRWVmbVvn79+srMzLR8/nUQ3Lx5s3r37q1GjRqpTp06atGihR5//HEdPXpUY8eOrXRMf7lI/x37wYMHVziXhIQE2djY6Mknn7z+gammCxcuyMPDQykpKZVuHz9+vBo3bqzS0lJJP49n+/bt5eDgID8/P6vxAwAAqPE7vb169dKhQ4esFh8fn5t6TBcXFzVo0OCm9F23bl0tXrzYat3s2bPl7e1dafvdu3frvffeq3L/x44dU48ePeTu7q7ly5ersLBQGRkZ8vT01JkzZzRixAirsWzWrJleffVVq3WXeHl5acGCBTp37pxl3fnz5zV//vzL1vtbsbe318CBA5WRkVFhm2EYyszMVExMjOzs7LRnzx5FRkYqLCxM+fn5SkxMVHx8vJYvX14DlQMAgFtRjYdeBwcHNWnSxGqZMmWKAgMD5ezsLC8vLz377LM6ffq0ZZ99+/YpKipKbm5ucnZ2Vps2bbR06VKrfvPy8tShQwc5OTmpS5cu2r59u2Xbr6c3lJeX69VXX1WzZs3k4OCg4OBgLVu2zLJ97969srGxUXZ2tsLCwuTk5KR27dpp3bp1Fc5n0KBBmjNnjuXzuXPntGDBAg0aNKjS83/uueeUlJSkkpKSKo1Xbm6uioqKNGvWLIWEhMjHx0dhYWF688035ePjIxcXF6uxrF27turWrWu17pL27dvLy8tL2dnZlnXZ2dny9vZWSEiI1XFLSko0dOhQy93l+++/Xxs2bLBqs3TpUvn7+8vR0VFhYWHau3dvhfpzcnL0wAMPyNHRUV5eXho6dKjOnDlT6bnGxcVpx44dysnJsVq/Zs0a7d69W3FxcZKk9PR0+fj4KC0tTa1bt9aQIUP06KOP6s0337zsOJaUlKi4uNhqAQAA5lXjobcytWrV0tSpU/Xdd99p7ty5WrVqlUaNGmXZnpCQoJKSEn355ZcqKChQamqqXFxcrPp46aWXlJaWpo0bN8rW1laxsbGXPd6UKVOUlpamyZMna8uWLQoPD1fv3r21c+fOCn2OGDFC+fn58vf3V//+/XXx4kWrNtHR0frqq6+0f/9+SVJWVpZatGih9u3bV3rsxMREXbx4UdOmTavS2DRp0kQXL17U4sWLZRhGlfa5ktjYWKu7qXPmzNFTTz1Vod2oUaOUlZWluXPnatOmTfLz81N4eLhOnDghSTpw4ID69OmjqKgo5efnKz4+XmPGjLHqY9euXerVq5ceeeQRbdmyRQsXLlROTo6GDBlSaW2BgYG69957rb5ESFJGRoa6dOmiVq1aSZLWrVunnj17WrUJDw+v9EvJJcnJyapXr55l8fLyusIoAQCA212Nh94lS5bIxcXFsvTt21eJiYkKCwtTixYt1L17d02YMEGLFi2y7LN//36FhoYqMDBQd999tx588EF17drVqt+JEyeqW7duCggI0JgxY7R27doKc20vmTx5skaPHq1+/frpnnvuUWpqqoKDgys8UDVixAhFRkbK399f48aN0759+yrMP27UqJEiIiIsc0rnzJlzxcDt5OSkpKQkJScnq6io6Krj1alTJ7344ot64okn5OHhoYiICE2aNElHjhy56r6VGThwoHJycrRv3z7t27dPubm5GjhwoFWbM2fOaMaMGZo0aZIiIiIUEBCgmTNnytHRUbNnz5YkzZgxQ76+vkpLS9M999yjAQMGVJgTnJycrAEDBigxMVEtW7ZUly5dNHXqVL333nuXvTZxcXH64IMPLHf6T506pQ8//NBqTA8fPqzGjRtb7de4cWMVFxdbTd34pRdeeEFFRUWW5cCBA9c0bgAA4PZS46H30jzMS8vUqVP1+eefq0ePHmratKnq1q2r6OhoHT9+XGfPnpUkDR06VBMmTFBoaKiSkpK0ZcuWCv0GBQVZfr7rrrskSUePHq3Qrri4WAcPHlRoaKjV+tDQUBUWFlarz9jYWGVmZmr37t1at26dBgwYcMUxiIuLU4MGDZSamnrFdpdMnDhRhw8fVnp6utq0aaP09HS1atVKBQUFVdr/lxo2bKjIyEhlZmYqIyNDkZGR8vDwsGqza9culZaWWo2RnZ2dOnbsaBmjwsJC3XfffVb7de7c2erz5s2blZmZafUlJzw8XOXl5dqzZ0+l9fXv319lZWWWLz0LFy5UrVq19Pjjj1/zuf6Sg4ODXF1drRYAAGBeNR56nZ2d5efnZ1lKSkr04IMPKigoSFlZWcrLy9Pbb78t6ecn+iUpPj5eu3fvVnR0tAoKCtShQ4cK0wPs7OwsP196Y0F5efl11VrVPiMiInTu3DnFxcUpKirqqg/N2draauLEiZoyZYoOHjxYpVoaNGigvn37avLkySosLJSnp6cmT558DWfzX5dC+ty5c694V/p6nT59Wk8//bTVl5zNmzdr586d8vX1rXQfV1dXPfroo5YpGBkZGXrsscesprM0adKkwp3uI0eOyNXVVY6OjjftfAAAwO2jxkPvr+Xl5am8vFxpaWnq1KmT/P39Kw2CXl5eGjx4sLKzszV8+HDNnDmzWsdzdXWVp6encnNzrdbn5uYqICCgWn3a2toqJiZGq1evrnKI7Nu3r9q0aaNx48Zd8/Hs7e3l6+t72QfCrqZXr166cOGCSktLFR4eXmG7r6+v7O3trcaotLRUGzZssIxR69at9c0331jtt379eqvP7du317Zt26y+5Fxa7O3tL1tfXFyccnJytGTJEq1du9byANslnTt3rvAKuhUrVlS40wwAAO5ctjVdwK/5+fmptLRU06ZNU1RUlHJzc5Wenm7VJjExUREREfL399fJkyf1xRdfqHXr1tU+5siRI5WUlCRfX18FBwcrIyND+fn5mjdvXrX7HD9+vEaOHHlNr0ZLSUmpNHT+0pIlS7RgwQL169dP/v7+MgxDn376qZYuXVrp672qonbt2pZpCrVr166w3dnZWc8884xGjhwpd3d3eXt76/XXX9fZs2ctAXTw4MFKS0vTyJEjFR8fr7y8vArvyh09erQ6deqkIUOGKD4+Xs7Oztq2bZtWrFih6dOnX7a+rl27ys/PTzExMWrVqpW6dOlitX3w4MGaPn26Ro0apdjYWK1atUqLFi3SZ599Vq3xAAAA5nPL3elt166d3njjDaWmpqpt27aaN2+ekpOTrdqUlZUpISFBrVu3Vq9eveTv76933nmn2sccOnSohg0bpuHDhyswMFDLli3TJ598opYtW1a7T3t7e3l4eFj9Qoqr6d69u7p3717hjRC/FBAQICcnJw0fPlzBwcHq1KmTFi1apFmzZik6Orra9V5tXmtKSooeeeQRRUdHq3379vr++++1fPlyubm5SZK8vb2VlZWljz76SO3atVN6erpee+01qz6CgoK0Zs0a7dixQw888IBCQkL0t7/9TZ6enleszcbGRrGxsTp58mSld859fHz02WefacWKFWrXrp3S0tI0a9asq36BAAAAdw4b40a89wq4zRUXF//86rLERarl4FTT5QAAcNPtTYms6RKu26W/v4uKiq76UPotd6cXAAAAuNEIvQAAADA9Qi8AAABMj9ALAAAA0yP0AgAAwPQIvQAAADA9Qi8AAABMj9ALAAAA0yP0AgAAwPQIvQAAADA9Qi8AAABMj9ALAAAA0yP0AgAAwPQIvQAAADA9Qi8AAABMj9ALAAAA0yP0AgAAwPQIvQAAADA9Qi8AAABMj9ALAAAA0yP0AgAAwPQIvQAAADA9Qi8AAABMz7amCwBuJVvHhcvV1bWmywAAADcYd3oBAABgeoReAAAAmB6hFwAAAKZH6AUAAIDpEXoBAABgeoReAAAAmB6hFwAAAKZH6AUAAIDpEXoBAABgeoReAAAAmB6hFwAAAKZH6AUAAIDpEXoBAABgeoReAAAAmB6hFwAAAKZH6AUAAIDpEXoBAABgeoReAAAAmB6hFwAAAKZH6AUAAIDpEXoBAABgeoReAAAAmB6hFwAAAKZH6AUAAIDpEXoBAABgeoReAAAAmB6hFwAAAKZH6AUAAIDpEXoBAABgerY1XQBwKzAMQ5JUXFxcw5UAAICquvT39qW/x6+E0AtIOn78uCTJy8urhisBAADX6tSpU6pXr94V2xB6AUnu7u6SpP3791/1fxrUrOLiYnl5eenAgQNydXWt6XJwBVyr2wfX6vbBtbJmGIZOnTolT0/Pq7Yl9AKSatX6eXp7vXr1+EPkNuHq6sq1uk1wrW4fXKvbB9fqv6p6s4oH2QAAAGB6hF4AAACYHqEXkOTg4KCkpCQ5ODjUdCm4Cq7V7YNrdfvgWt0+uFbVZ2NU5R0PAAAAwG2MO70AAAAwPUIvAAAATI/QCwAAANMj9AIAAMD0CL2ApLffflstWrRQnTp1dN999+mbb76p6ZLueMnJybr33ntVt25dNWrUSH/605+0fft2qzbnz59XQkKCGjRoIBcXFz3yyCM6cuRIDVUMSUpJSZGNjY0SExMt67hOt44ff/xRAwcOVIMGDeTo6KjAwEBt3LjRst0wDP3tb3/TXXfdJUdHR/Xs2VM7d+6swYrvTGVlZXrllVfk4+MjR0dH+fr6avz48frluwe4VteO0Is73sKFCzVs2DAlJSVp06ZNateuncLDw3X06NGaLu2OtmbNGiUkJGj9+vVasWKFSktL9Yc//EFnzpyxtPnrX/+qTz/9VB988IHWrFmjgwcPqk+fPjVY9Z1tw4YN+vvf/66goCCr9VynW8PJkycVGhoqOzs7/fOf/9S2bduUlpYmNzc3S5vXX39dU6dOVXp6ur7++ms5OzsrPDxc58+fr8HK7zypqamaMWOGpk+frsLCQqWmpur111/XtGnTLG24VtVgAHe4jh07GgkJCZbPZWVlhqenp5GcnFyDVeHXjh49akgy1qxZYxiGYfz000+GnZ2d8cEHH1jaFBYWGpKMdevW1VSZd6xTp04ZLVu2NFasWGF069bNeP755w3D4DrdSkaPHm3cf//9l91eXl5uNGnSxJg0aZJl3U8//WQ4ODgY77///m9RIv5fZGSkERsba7WuT58+xoABAwzD4FpVF3d6cUe7cOGC8vLy1LNnT8u6WrVqqWfPnlq3bl0NVoZfKyoqkiS5u7tLkvLy8lRaWmp17Vq1aiVvb2+uXQ1ISEhQZGSk1fWQuE63kk8++UQdOnRQ37591ahRI4WEhGjmzJmW7Xv27NHhw4etrlW9evV03333ca1+Y126dNHKlSu1Y8cOSdLmzZuVk5OjiIgISVyr6rKt6QKAmvSf//xHZWVlaty4sdX6xo0b69///ncNVYVfKy8vV2JiokJDQ9W2bVtJ0uHDh2Vvb6/69etbtW3cuLEOHz5cA1XeuRYsWKBNmzZpw4YNFbZxnW4du3fv1owZMzRs2DC9+OKL2rBhg4YOHSp7e3sNGjTIcj0q+/OQa/XbGjNmjIqLi9WqVSvVrl1bZWVlmjhxogYMGCBJXKtqIvQCuOUlJCRo69atysnJqelS8CsHDhzQ888/rxUrVqhOnTo1XQ6uoLy8XB06dNBrr70mSQoJCdHWrVuVnp6uQYMG1XB1+KVFixZp3rx5mj9/vtq0aaP8/HwlJibK09OTa3UdmN6AO5qHh4dq165d4UnyI0eOqEmTJjVUFX5pyJAhWrJkib744gs1a9bMsr5Jkya6cOGCfvrpJ6v2XLvfVl5eno4ePar27dvL1tZWtra2WrNmjaZOnSpbW1s1btyY63SLuOuuuxQQEGC1rnXr1tq/f78kWa4Hfx7WvJEjR2rMmDHq16+fAgMDFR0drb/+9a9KTk6WxLWqLkIv7mj29vb63e9+p5UrV1rWlZeXa+XKlercuXMNVgbDMDRkyBAtXrxYq1atko+Pj9X23/3ud7Kzs7O6dtu3b9f+/fu5dr+hHj16qKCgQPn5+ZalQ4cOGjBggOVnrtOtITQ0tMJr/3bs2KHmzZtLknx8fNSkSROra1VcXKyvv/6aa/UbO3v2rGrVso5otWvXVnl5uSSuVbXV9JN0QE1bsGCB4eDgYGRmZhrbtm0z/vKXvxj169c3Dh8+XNOl3dGeeeYZo169esbq1auNQ4cOWZazZ89a2gwePNjw9vY2Vq1aZWzcuNHo3Lmz0blz5xqsGoZhWL29wTC4TreKb775xrC1tTUmTpxo7Ny505g3b57h5ORk/OMf/7C0SUlJMerXr298/PHHxpYtW4yHHnrI8PHxMc6dO1eDld95Bg0aZDRt2tRYsmSJsWfPHiM7O9vw8PAwRo0aZWnDtbp2hF7AMIxp06YZ3t7ehr29vdGxY0dj/fr1NV3SHU9SpUtGRoalzblz54xnn33WcHNzM5ycnIyHH37YOHToUM0VDcMwKoZertOt49NPPzXatm1rODg4GK1atTLeffddq+3l5eXGK6+8YjRu3NhwcHAwevToYWzfvr2Gqr1zFRcXG88//7zh7e1t1KlTx7j77ruNl156ySgpKbG04VpdOxvD+MWv9wAAAABMiDm9AAAAMD1CLwAAAEyP0AsAAADTI/QCAADA9Ai9AAAAMD1CLwAAAEyP0AsAAADTI/QCAADA9Ai9AADcAF27dtX8+fOvq49OnTopKyvrBlUE4JcIvQAAXKdPPvlER44cUb9+/Szrhg0bJnd3d3l5eWnevHlW7T/44ANFRUVV6Ofll1/WmDFjVF5eftNrBu40/BpiAIAplJaWys7OrkaO3bNnT/Xs2VNjxoyRJH366af685//rCVLlmjnzp2KjY3VgQMH5OHhoaKiIt177736/PPP5e3tbdVPWVmZmjZtqtmzZysyMrImTgUwLe70AgCu2bJly3T//ferfv36atCggR588EHt2rXLqs0PP/yg/v37y93dXc7OzurQoYO+/vpry/ZPP/1U9957r+rUqSMPDw89/PDDlm02Njb66KOPrPqrX7++MjMzJUl79+6VjY2NFi5cqG7duqlOnTqaN2+ejh8/rv79+6tp06ZycnJSYGCg3n//fat+ysvL9frrr8vPz08ODg7y9vbWxIkTJUndu3fXkCFDrNofO3ZM9vb2WrlyZaVjcezYMa1atcrqzm1hYaH+53/+Rx06dFD//v3l6uqqPXv2SJJGjRqlZ555pkLglaTatWvrj3/8oxYsWFDpsQBUH6EXAHDNzpw5o2HDhmnjxo1auXKlatWqpYcfftjyz/KnT59Wt27d9OOPP+qTTz7R5s2bNWrUKMv2zz77TA8//LD++Mc/6ttvv9XKlSvVsWPHa65jzJgxev7551VYWKjw8HCdP39ev/vd7/TZZ59p69at+stf/qLo6Gh98803ln1eeOEFpaSk6JVXXtG2bds0f/58NW7cWJIUHx+v+fPnq6SkxNL+H//4h5o2baru3btXWkNOTo6cnJzUunVry7p27dpp48aNOnnypPLy8nTu3Dn5+fkpJydHmzZt0tChQy97Th07dtRXX311zWMB4CoMAACu07FjxwxJRkFBgWEYhvH3v//dqFu3rnH8+PFK23fu3NkYMGDAZfuTZCxevNhqXb169YyMjAzDMAxjz549hiTjrbfeumptkZGRxvDhww3DMIzi4mLDwcHBmDlzZqVtz507Z7i5uRkLFy60rAsKCjLGjh172f7ffPNN4+67766wPikpyfD19TXatm1rZGdnGyUlJUbbtm2NjRs3GtOmTTP8/f2NLl26GFu3brXa7+OPPzZq1apllJWVXfXcAFQdd3oBANds586d6t+/v+6++265urqqRYsWkqT9+/dLkvLz8xUSEiJ3d/dK98/Pz1ePHj2uu44OHTpYfS4rK9P48eMVGBgod3d3ubi4aPny5Za6CgsLVVJSctlj16lTR9HR0ZozZ44kadOmTdq6dauefPLJy9Zw7tw51alTp8L6sWPH6vvvv1dBQYEefvhhJScnq2fPnrKzs9OECROUk5Oj+Ph4xcTEWO3n6Oio8vJyq7vNAK6fbU0XAAC4/URFRal58+aaOXOmPD09VV5errZt2+rChQuSfg5uV3K17TY2NjJ+9Zx1aWlphXbOzs5WnydNmqQpU6borbfeUmBgoJydnZWYmFjluqSfpzgEBwfrhx9+UEZGhrp3767mzZtftr2Hh4dOnjx5xT7//e9/6x//+Ie+/fZbzZkzR127dlXDhg312GOPKTY2VqdOnVLdunUlSSdOnJCzs3OVagVQddzpBQBck+PHj2v79u16+eWX1aNHD7Vu3bpC6AsKClJ+fr5OnDhRaR9BQUGXfTBMkho2bKhDhw5ZPu/cuVNnz569am25ubl66KGHNHDgQLVr10533323duzYYdnesmVLOTo6XvHYgYGB6tChg2bOnKn58+crNjb2iscMCQnR4cOHLxt8DcPQ008/rTfeeEMuLi4qKyuzBPhL/y0rK7O037p1q0JCQq56rgCuDaEXAHBN3Nzc1KBBA7377rv6/vvvtWrVKg0bNsyqTf/+/dWkSRP96U9/Um5urnbv3q2srCytW7dOkpSUlKT3339fSUlJKiwsVEFBgVJTUy37d+/eXdOnT9e3336rjRs3avDgwVV6HVnLli21YsUKrV27VoWFhXr66ad15MgRy/Y6depo9OjRGjVqlN577z3t2rVL69ev1+zZs636iY+PV0pKigzDsHqrRGVCQkLk4eGh3NzcSrfPmjVLDRs2tLzdITQ0VKtWrdL69ev15ptvKiAgQPXr17e0/+qrr/SHP/zhqucK4BrV8JxiAMBtaMWKFUbr1q0NBwcHIygoyFi9enWFh8/27t1rPPLII4arq6vh5ORkdOjQwfj6668t27Oysozg4GDD3t7e8PDwMPr06WPZ9uOPPxp/+MMfDGdnZ6Nly5bG0qVLK32Q7dtvv7Wq6/jx48ZDDz1kuLi4GI0aNTJefvllIyYmxnjooYcsbcrKyowJEyYYzZs3N+zs7Axvb2/jtddes+rn1KlThpOTk/Hss89WaTxGjRpl9OvXr8L6w4cPG82bNzd+/PFHq/Xjxo0z3N3djVatWlmNyQ8//GDY2dkZBw4cqNJxAVQdv5wCAIBf2bt3r3x9fbVhwwa1b9/+qu0PHz6sNm3aaNOmTVec/3s1o0eP1smTJ/Xuu+9Wuw8AlWN6AwAA/6+0tFSHDx/Wyy+/rE6dOlUp8EpSkyZNNHv2bMtbIqqrUaNGGj9+/HX1AaBy3OkFAOD/rV69WmFhYfL399eHH36owMDAmi4JwA1C6AUAAIDpMb0BAAAApkfoBQAAgOkRegEAAGB6hF4AAACYHqEXAAAApkfoBQAAgOkRegEAAGB6hF4AAACY3v8BNb6X91LnJdoAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# Visualize our model results\n",
"compare_results.set_index(\"model_name\")[\"model_acc\"].plot(kind=\"barh\")\n",
"plt.xlabel(\"accuracy (%)\")\n",
"plt.ylabel(\"model\");"
]
},
{
"cell_type": "markdown",
"id": "0ba50d51-adb3-4e49-9b9a-85173e747352",
"metadata": {
"id": "0ba50d51-adb3-4e49-9b9a-85173e747352"
},
"source": [
"## 9. Make and evaluate random predictions with best model\n",
"\n",
"Alright, we've compared our models to each other, let's further evaluate our best performing model, `model_2`.\n",
"\n",
"To do so, let's create a function `make_predictions()` where we can pass the model and some data for it to predict on."
]
},
{
"cell_type": "code",
"execution_count": 46,
"id": "d1d5d3e7-9601-4141-8bd7-9abbd016bf6c",
"metadata": {
"id": "d1d5d3e7-9601-4141-8bd7-9abbd016bf6c"
},
"outputs": [],
"source": [
"def make_predictions(model: torch.nn.Module, data: list, device: torch.device = device):\n",
" pred_probs = []\n",
" model.eval()\n",
" with torch.inference_mode():\n",
" for sample in data:\n",
" # Prepare sample\n",
" sample = torch.unsqueeze(sample, dim=0).to(device) # Add an extra dimension and send sample to device\n",
"\n",
" # Forward pass (model outputs raw logit)\n",
" pred_logit = model(sample)\n",
"\n",
" # Get prediction probability (logit -> prediction probability)\n",
" pred_prob = torch.softmax(pred_logit.squeeze(), dim=0) # note: perform softmax on the \"logits\" dimension, not \"batch\" dimension (in this case we have a batch size of 1, so can perform on dim=0)\n",
"\n",
" # Get pred_prob off GPU for further calculations\n",
" pred_probs.append(pred_prob.cpu())\n",
" \n",
" # Stack the pred_probs to turn list into a tensor\n",
" return torch.stack(pred_probs)"
]
},
{
"cell_type": "code",
"execution_count": 47,
"id": "420c7461-eaa9-4459-9e68-53574c758765",
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/"
},
"id": "420c7461-eaa9-4459-9e68-53574c758765",
"outputId": "f3dd6437-4f0f-4bc2-f9e6-d0969df63a52"
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Test sample image shape: torch.Size([1, 28, 28])\n",
"Test sample label: 5 (Sandal)\n"
]
}
],
"source": [
"import random\n",
"random.seed(42)\n",
"test_samples = []\n",
"test_labels = []\n",
"for sample, label in random.sample(list(test_data), k=9):\n",
" test_samples.append(sample)\n",
" test_labels.append(label)\n",
"\n",
"# View the first test sample shape and label\n",
"print(f\"Test sample image shape: {test_samples[0].shape}\\nTest sample label: {test_labels[0]} ({class_names[test_labels[0]]})\")"
]
},
{
"cell_type": "code",
"execution_count": 48,
"id": "1DYqA0r4SkrV",
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/"
},
"id": "1DYqA0r4SkrV",
"outputId": "97bc573d-b39b-4eb2-caad-0379257b555e"
},
"outputs": [
{
"data": {
"text/plain": [
"tensor([[2.4012e-07, 6.5406e-08, 4.8069e-08, 2.1070e-07, 1.4175e-07, 9.9992e-01,\n",
" 2.1711e-07, 1.6177e-05, 3.7849e-05, 2.7548e-05],\n",
" [1.5646e-02, 8.9752e-01, 3.6928e-04, 6.7402e-02, 1.2920e-02, 4.9539e-05,\n",
" 5.6485e-03, 1.9456e-04, 2.0808e-04, 3.7861e-05]])"
]
},
"execution_count": 48,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Make predictions on test samples with model 2\n",
"pred_probs= make_predictions(model=model_2, \n",
" data=test_samples)\n",
"\n",
"# View first two prediction probabilities list\n",
"pred_probs[:2]"
]
},
{
"cell_type": "markdown",
"id": "e9f40dd9-7987-42a9-84cc-65dc912a6345",
"metadata": {
"id": "e9f40dd9-7987-42a9-84cc-65dc912a6345"
},
"source": [
"And now we can use our `make_predictions()` function to predict on `test_samples`."
]
},
{
"cell_type": "code",
"execution_count": 49,
"id": "79de2ac1-7d4b-4f81-ae8a-90099bca2a3d",
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/"
},
"id": "79de2ac1-7d4b-4f81-ae8a-90099bca2a3d",
"outputId": "918b07bc-4545-4401-84d5-8796ff5acf4c"
},
"outputs": [
{
"data": {
"text/plain": [
"tensor([[2.4012e-07, 6.5406e-08, 4.8069e-08, 2.1070e-07, 1.4175e-07, 9.9992e-01,\n",
" 2.1711e-07, 1.6177e-05, 3.7849e-05, 2.7548e-05],\n",
" [1.5646e-02, 8.9752e-01, 3.6928e-04, 6.7402e-02, 1.2920e-02, 4.9539e-05,\n",
" 5.6485e-03, 1.9456e-04, 2.0808e-04, 3.7861e-05]])"
]
},
"execution_count": 49,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Make predictions on test samples with model 2\n",
"pred_probs= make_predictions(model=model_2, \n",
" data=test_samples)\n",
"\n",
"# View first two prediction probabilities list\n",
"pred_probs[:2]"
]
},
{
"cell_type": "markdown",
"id": "22d3c080-4eb6-4b5d-a5c4-2319e78228af",
"metadata": {
"id": "22d3c080-4eb6-4b5d-a5c4-2319e78228af"
},
"source": [
"Excellent!\n",
"\n",
"And now we can go from prediction probabilities to prediction labels by taking the `torch.argmax()` of the output of the `torch.softmax()` activation function."
]
},
{
"cell_type": "code",
"execution_count": 50,
"id": "f9d97bcc-4310-4851-a1f8-6bcd757e9b26",
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/"
},
"id": "f9d97bcc-4310-4851-a1f8-6bcd757e9b26",
"outputId": "9d0f0bf9-a641-45e7-af77-6621fd1cfcc4"
},
"outputs": [
{
"data": {
"text/plain": [
"tensor([5, 1, 7, 4, 3, 0, 4, 7, 1])"
]
},
"execution_count": 50,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Turn the prediction probabilities into prediction labels by taking the argmax()\n",
"pred_classes = pred_probs.argmax(dim=1)\n",
"pred_classes"
]
},
{
"cell_type": "code",
"execution_count": 51,
"id": "1141af97-0990-4920-83d4-c13cca3f9abc",
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/"
},
"id": "1141af97-0990-4920-83d4-c13cca3f9abc",
"outputId": "c69cddd4-bbe9-495e-d477-6ea0a6c7d8de"
},
"outputs": [
{
"data": {
"text/plain": [
"([5, 1, 7, 4, 3, 0, 4, 7, 1], tensor([5, 1, 7, 4, 3, 0, 4, 7, 1]))"
]
},
"execution_count": 51,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Are our predictions in the same form as our test labels? \n",
"test_labels, pred_classes"
]
},
{
"cell_type": "markdown",
"id": "4ea04387-c9ad-424f-8297-defd7b685683",
"metadata": {
"id": "4ea04387-c9ad-424f-8297-defd7b685683"
},
"source": [
"Now our predicted classes are in the same format as our test labels, we can compare.\n",
"\n",
"Since we're dealing with image data, let's stay true to the data explorer's motto. \n",
"\n",
"\"Visualize, visualize, visualize!\""
]
},
{
"cell_type": "code",
"execution_count": 52,
"id": "679cb5f7-bb66-42dd-a4d6-400b27b7c019",
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/",
"height": 749
},
"id": "679cb5f7-bb66-42dd-a4d6-400b27b7c019",
"outputId": "3aae0abe-9c19-4054-d8db-7e00403666aa"
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAt0AAALcCAYAAAA7awxXAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/bCgiHAAAACXBIWXMAAA9hAAAPYQGoP6dpAACNV0lEQVR4nO3dd3gVZfr/8U8S0qv0TmhSLHSsCGIBEUXEzoqIFfva9bsqWNHFte2Kq6xgWUV3RVDqIhIEFEGRIgSkBRBDCwQICem/P/LjaIDnnnDCQALv13V5XZL7zDNz5swzc2fOOZ+EFBcXFwsAAACAb0KP9gYAAAAAxzqabgAAAMBnNN0AAACAz2i6AQAAAJ/RdAMAAAA+o+kGAAAAfEbTDQAAAPiMphsAAADwGU03AAAA4DOabgAAAMBnla7pHjhuoC4bc9nR3owyO9TtTctMU8jQEC3ctND5mNELR6vb6G7l3rbDYfTC0UoalnS0N6NchqQMUdu32h7SMiFDQzRu+Thftud4Udnmst9S0lKU/Gry0d4MSSXbEjI0RJl7M4/2pqCCqszztyzX2cOF67W/Ktu1uMrhGGTguIF6b9F7kqTw0HA1TGyoAW0G6PEuj6tK6GFZRbls3bNVT854UhNXTtTmPZt1QtQJalO7jZ4850md1fCso715h1VaZpoav9bYfMyoPqM0sO3AQx47+dVk3Xf6fbrv9PuC2zhDdn62npn5jD5d9qk27tqo+Mh4ta7RWveffr/6tOxz2NeHg6vIczlkaIhZf6rrUxrSbciR2ZijwK/n3210N7Wt3Vav9nw1uA0zxp25bqaz3rVRV6UMTDms6zzeVeT5Kx1f1+Ky4Hp9/Dlss7Bns54a1WeUcgtyNWnlJN056U6Fh4brsS6PHfDYvMI8RYRFHK5Ve+r3aT/lFebpvcveU5MTmmjzns2avma6MnIyjtg2HCkNEhoo/YH0wL+HfztcU1ZN0VcDvgr8LDEyMfD/hUWFCgkJUWjI0X3T4/YJt+v7jd/rjYveUOsarZWRnaFvN3x7TL5GFV1Fnct/PK4/+fkTPZnypFbctSLws7iIuMD/FxcXq7C4sEI0GvsLdp9Vtuc/9uqxyivMkyRt2LlBnUd21lfXf6WTap4kSQfsg/zCfIWHhR/x7fRypK9X5VVR5690bF+Lgzl+uV5XPH7PicP2ykWGRap2XG01SmqkwZ0G6/wm5+uLX76Q9PvbUM9985zqvlxXLf7eQlLJifiq/1ylpGFJqvpiVfUZ00dpmWmBMQuLCnX/1PuVNCxJ1V6qpoenPaxiFR/SdmXuzdSs9bP04vkv6tzG56pRUiN1rtdZj3V5TJe2uDTwuL999zedMuIUxT4fqwavNNAdE+9QVl5WoL7vbZmpq6aq1T9aKe75OPX8sKfSd/8+YcqyvVNWTdHZ754deEzvj3pr9fbVh/ScLGGhYaodVzvwX1xEnKqEVgn8e8qqKarzch19seILtf5Ha0U+G6n1O9er2+huum/KfaXGumzMZRo4bqCkkrtW63au05+n/lkhQ0MOuOtm7Zey+GLFF3r87MfVq3kvJSclq0PdDrr7tLs1qN2gwGM+WPSBOr7dUfEvxKv28Nq67rPrtGXPlkB931vi09dMV8e3OyrmuRid+a8ztWLbilLrGjZ7mGoNr6X4F+J10/ibtLdgb6n6/I3zdcEHF6j6S9WVOCxRXUd31YL0BYf0fCqzijqX/3hcJ0YlKkQhgX8v37Zc8S/Ea/LKyerwdgdFPhup2etnK7cgV/dMvkc1/1pTUc9G6ex3z9b8jfMDYx7s7dZxy8eVOr4XbVqkc987V/EvxCvhhQR1eLuDfvjth0B99vrZ6jKqi6Kfi1aDVxronsn3aE/enkA9+dVkPTPzGQ34fIASXkjQrV/eekjPuzzP/2AfAbhvyn2Bt7sHjhuometm6rXvXwvM6z++bj/+9qM5lyxVo6sGtq9GbA1JUrWYaoGfVXupmkbMH6FLP75Usc/H6rlZz0mSRswfoaavN1XEMxFq8fcW+mDRB4ExD/axgMy9mQoZGqKUtBRJ0o6cHeo/tr9q/LWGop+LVvM3mmvUT6MCj/c6Vl3HeGVRUedvWa/FIUNDNHLBSPX9pK9inotR8zea64sVX5Qa6+ctP+uif1+kuOfjVGt4LV3/+fXalr0tUD/U62xhUaEGjR+kln9vqfU710uSxi8fr/b/bK+oZ6PU5LUmGpoyVAVFBaW282DH76E4lq/Xya8m6/lZz2vQ+EGKfyFeDV9pqLd/fLvUOF7HXTDX4qdmPKU6L9fR4s2LJR2583NZ+fbrUnR4dOAuhyRNXztdKzJWaNr10zTh2gnKL8xXjw97KD4iXrNunKU5g+YoLqLkANi33MvfvazRC0fr3T7vavaNs7U9Z7s+T/281HpGLxxtvu0aFxGnuIg4jVs+TrkFuc7HhYaE6vWer2vpHUv13mXv6eu1X+vhaQ+Xekx2fraGfzdcH/T9QN/c+I3W71yvB6c9GKiXZXv35O3R/Wfcrx9u/UHTB0xXaEio+n7SV0XFRd479TDJzs/Wi3Ne1MhLR2rpHUtVM7am5zJjrx6r+gn19XS3p5X+QHqp38699su+ZviPk2l/teNqa9KqSdqdu9v5mPyifD1z7jNadPsijbtmnNIy0wInmT/6v6//Ty9f+LJ+uPUHVQmtokFf/H4i+HTppxqSMkTPd39eP9zyg+rE19Gb898stfzuvN26oc0Nmj1otubeNFfNqzZXr3/3MrftWFZR5nJZPDr9UQ07b5hS70zVqbVO1cPTHtZnqZ/pvcve04LbFqhZ1Wbq8WEPbc/ZXuYx+4/tr/oJ9TX/lvn68dYf9ehZjyo8tOSO1urtq9Xzw57q16qfFt++WJ9c8Ylmr5+tuybfVWqM4d8NV5tabfTTbT/piXOeKNdztOz//L281vM1nVH/DN3S/pbAvG6Q0CBQt+bSvgZ4X7MbjCEzh6hvy75aMniJBrUbpM9TP9e9U+7VA2c8oJ/v+Fm3dbhNN46/UTPWzijzmE/MeELLti7T5P6TlXpnqkZcPELVY6pLUpmOVenAY7wyqyjzt6zXYkkaOnOormp9lRYPXqxezXqp/9j+gTmbuTdT3d/rrna12+mHW3/QlP5TtDlrs676z1WB5Q/lOptbkKsr/3OlFm5aqFk3zlLDxIaatW6WBowboHtPu1fL7lymf/b+p0YvGq3nvindWO9//Pqhsl6vpZLjpmPdjvrptp90R6c7NHji4MAv7mU57g7lWlxcXKy7J92t9xe/r1k3ztKptU6tcOdn6TB+vGSf4uJiTV87XVNXTdXdne8O/Dw2PFYjLx0ZuG3/4eIPVVRcpJGXjlRISMlEHdVnlJKGJSklLUUXNr1Qr859VY+d/Zgub3W5JOmt3m9p6uqppdaXGJmoFtXcdyKqhFbR6D6jdcuXt+itH99S+zrt1bVRV11z8jWlLkp//NxTclKynu3+rG6fcLvevPj3hiy/KF9vXfyWmlZtKkm6q/Ndenrm04F6Wba3X+t+pf79bp93VeOvNbRs6zKdXPNk5/M4nPKL8vVmrzfVpnabMi9TNbqqwkLCFB8Zr9pxtQ8Yz9ovMeExalGtRaBROZi3L3lb/cf2V7WXqqlN7TY6u8HZuqL1FaU+5/fHk1qTE5ro9YteV6d3OikrL6vUW+vPdX9OXZO7SpIePftRXfzRxdpbsFdRVaL06txXdVO7m3RT+5skSc92f1Zfrfmq1N3u7o27H7BtScOSNHPdTPU+sXeZ91llV9Hmclk83e1pXdD0AkklF94RP4zQ6MtG66LmF0mS3rnkHU1bM03/WvAvPXTWQ2Uac/3O9XrozIfUsnpLSVLzas0DtRdmv6D+p/QPnD+aV2uu1y96XV1Hd9WIi0coqkqUpJJj6oEzHyjXcyuLPz7/skiMSlREWIRiwmMOmNeSPZfCQ8PVoloLxYTHBL291518nW5sd2Pg39d+dq0Gth2oOzrdIUm6/4z7NffXuRr+3XCd2/jcMo25fud6tavdTh3rdpRUcj7f55Oln3geq9KBx3hlVNHmb1mvxZI0sM1AXXvKtZKk5897Xq/Pe13zNs5Tz2Y99fd5f1e7Ou30/HnPBx7/bp931eCVBvol4xedWO3EMl9ns/KydPFHFyu3MFczbpihxKiSj3IMnTlUj571qG5oe4OkkuvNM+c+o4enPaynuj0VWH7/49cPlfV6LUm9mvcKzOVHznpEr8x9RTPSZqhF9RZlmotlvRYXFBXoT5//ST+l/6TZN85WvYR6kire+Vk6jE33hF8mKO75OOUX5auouEjXnXJdqS/1nFLrlFInsEWbFmnV9lWKfyG+1Dh7C/Zq9fbV2llvp9Kz0nVa/dN+39jQKupYt6OKi39/W6tvq77q26qvuW39WvfTxSderFnrZmnur3M1edVkvTTnJY28dGTgCwpfrflKL8x+Qcu3Ldeu3F0qKCrQ3oK9ys7PDlxUYsJjAgeqJNWJqxP4eMPOvWXb3pUZK/VkypP6/tfvtS17W+A37/U71x+xpjsiLKJMd8HKytovktS5Xmctv2u5OcY5jc7RmnvWaO6vc/Xthm81fe10vTbqNQ3tNlRPdC35zfPH337UkJlDtGjTIu3Yu6PUvmtdo3VgrD8+tzpxdSRJW/ZsUcPEhkrdlqrbO95eat1n1D9DM9J+v5O2OWuz/vL1X5SyLkVb9mxRYVGhsvOzA287Husq8lz2sq/RkqTVO1YrvyhfZzX4/UIQHhauzvU6K3VbapnHvP+M+3Xzlzfrg8Uf6Pwm5+vK1lcGjvdFmxdp8ebF+veSfwceX6xiFRUXae2OtWpVo1XJdtXpeNCxD7c/Pv/DwZpL9RLqec5rL/tvb+rWVN3avvTbu2c1OEuvff9amccc3HGw+n3aTwvSF+jCphfqspaX6cwGZ0ryPlb1/09j+x/jlUlFnr9luRZLpY+72IhYJUQmBK4pizYv0oy1MxT3fNz+w2v19tU6sdqJZb7OXvvZtaqfUF9fD/ha0eHRv++TzYs0Z8OcUh8ZKSwuPKAnONzz7WAq6/Vakk6t+ft2h4SUfBwu8DqWYS6W9Vr856l/VmRYpObePDfwrpZU8c7P0mFsus9tfK5GXDxCEWERqhtf94Av8MSGx5b6d1ZeljrU7aB/X/5v7a9GTI3DtVkBUVWidEHTC3RB0wv0RNcndPMXN+uplKc0sO1ApWWmqfdHvTW442A91/05VY2uqtnrZ+umL25SXmFeYILt/5tfSEjIIX+u7ZKPL1GjpEZ655J3VDe+roqKi3TyiJNLvf3nt+gq0YHfLPcJDQktdQKVSn4jLovDsV+kkoaoS6Mu6tKoix45+xE9+82zenrm03rk7EcCb0X1aNZD/77836oRW0Prd65Xjw97HLDv/vhlln3P81A+vnPDuBuUkZOh13q+pkaJjRRZJVJn/OuMI/oaHU0VfS5bYiNivR/0B6EhoQccq/mFpY/7Id2G6LpTrtPEXyZq8qrJeirlKY3pN0Z9W/VVVl6Wbutwm+457Z4Dxm6Y2DDo7QrW/uspy/OzlHcueQnm9ZJU6ly1//O5qPlFWnffOk1aOUnT1kzTee+fpzs73anhFw4v87G6/zFemVT0+Wtdi/fZ/wuJIQoJHHdZeVm6pMUlevH8Fw8Ye98vhmW9zvZq1ksfLvlQ3/36Xam7qll5WRrabWjgzv7+27/PkZjXlfF6ve+XOq/X0eu4K+u1+IImF+jjnz/W1FVT1f/U/oGfV7Tzs3QYm+7Y8Fg1q9qszI9vX6e9Pln6iWrG1lRCZMJBH1Mnro6+//V7ndPoHEklbyH8+NuPal+nfbm3t3WN1oFsxx9/+1FFxUV6ucfLgZP6p0s/PaTxEqMSPbc3IztDKzJW6J1L3lGXRl0klXzIvyKoEVtD6VmlvxT685afdW7y72/pRoRFqLCo8IhtU+sarQPvOKzMWKmMnAwNO2+YGiSWfOb0j19mK6tW1Vvp+1+/14A2AwI/m7txbqnHzNkwR2/2elO9mveSVPJljz9+SedYV9nmskvTE5oqIixCczbMUaOkRpJKGrT5G+cH3m6sEVNDu3N3a0/ensCJ92DZvSdWO1EnnnGi/nzGn3XtZ9dq1MJR6tuqr9rXaa9lW5cd0v46kmrE1NDPW34u9bOFmxeWuvAe6XltaVWjleZsmBN4W18qmY/73snadzFOz0pXO7WTdPDXq0ZsDd3Q9gbd0PYGdfmhix6a9pCGXzi8TMdqZVfZ5u8fr8Vl2t7a7fVZ6mdKTko+aDrPoVxnB3carJNrnqxLP75UE6+bGPgoVfs67bVi24qKO68r+PW6LO8SleW4K+u1+NIWl+qSEy/RdWOvU1homK45+ZrAOira+fmo5c70P7W/qsdUV58xfTRr3Syt3bFWKWkpumfyPfp116+SpHtPu1fD5gzTuOXjtHzbct0x8Y4D/ljD56mfq+XfWzrXk5Gdoe7vddeHiz/U4s2LtXbHWv1n6X/00pyX1KdFSZ5ks6rNlF+Urze+f0NrdqzRB4s+0Fs/vHXIz8lre0+IPkHVoqvp7QVva9X2Vfp67de6f+r9h7weP3RP7q6JKydq4i8TtXzbcg2eOPiAfZ2clKxv1n+jjbs2HlITOm/jPLX8e0tt3LXR+Zhuo7vpnz/8Uz/+9qPSMtM0aeUkPT79cZ3b+FwlRCaoYWJDRYRF6I15Ja/RFyu+0DPfPHPIz/Pe0+7Vuwvf1aifRumXjF/01IyntHTL0lKPaV61uT5Y/IFSt6bq+1+/V/+x/RVdJdoxIo7UXD5UsRGxGtxxsB6a9pCmrJqiZVuX6ZYvb1F2frZualfymf7T6p+mmPAYPT79ca3evlofLflIoxeNDoyRk5+juybdpZS0FK3LXKc56+do/sb5alW95G3JR856RN9u+FZ3TbpLCzct1MqMlRq/fLzumnTXwTbpiOveuLt++O0Hvb/ofa3MWKmnZjx1QBOenJSs7zd+r7TMtFJvxXvZuGujWv69peZtnHfYtvehMx/S6IWjNWL+CK3MWKm/ffc3jU0dqwfPLPmiV3R4tE6vf7qGzR6m1K2pmpk2U3+Z8ZdSYzw540mNXz5eq7av0tItSzVh5YTA28hlOVaPNxXpWlwWd3a+U9tztuvaz67V/I3ztXr7ak1dNVU3jr9RhUWFh3ydvfu0u/Vs92fV++Pegeb8yXOe1PuL39fQlKFaumWpUremaszPY/SXr//iHOdIqujX67Ioy3F3KNfivq366oO+H+jG8Tfqv8v+K6linp+PWohrTHiMvrnxGz3y1SO6/NPLtTt3t+ol1NN5jc8LvGgPnPmA0rPSdcO4GxQaEqpBbQepb6u+2rl3Z2Ccnbk7tSLDHWMVFxGn0+qdplfmvqLV20s+49kgoYFuaX+LHu/yuCSpTe02+tuFf9OLc17UY9Mf0zmNztEL572gAeMGOMc9GK/tDQ0J1Zgrxuieyffo5DdPVovqLfR6z9fV7b1uh7bzfDCo3SAt2rxIA8YNUJXQKvrz6X8u9VuzJD197tO6bcJtavp6U+UW5qr4qbK9JZWdn60VGSvMt796NO2h9xa9p8e/flzZ+dmqG19XvZv31pNdn5RU8pv96D6j9fjXj+v1719X+zrtNfyC4bp0zKXOMQ/m6pOv1uodq/XwVw9rb8Fe9WvVT4M7Di71paB/Xfov3TrhVrV/u70aJDTQ8+c9rwf/96Ax6vHtSM3lYAw7f5iKiot0/efXa3fubnWs21FT/zRVJ0SfIKnkC0cfXv6hHpr2kN5Z8I7Oa3KehnQdolsnlHyuOCw0TBk5GRrw+QBt3rNZ1WOq6/KWl2vouUMllXz2dObAmfq/r/9PXUZ1UXFxsZpWbaqrT7r6sD6PYPVo1kNPnPOEHp5WcrwPajdIA04doCVblgQe8+CZD+qGcTeo9T9aK6cgR2vvXVumsfOL8rUiY4Wy87MP2/Ze1vIyvdbzNQ3/brjunXKvGp/QWKP6jFK35G6Bx7x76bu66Yub1OHtDmpRvYVeOv8lXfjhhYF6RFiEHpv+mNIy0xQdHq0uDbtoTL8xksp2rB5vKtK1uCzqxtfVnEFz9MhXj+jCDy9UbkGuGiU1Us+mPRUaEqqQkJBDvs7ed/p9KiouUq9/99KUP01Rj2Y9NOHaCXr6m6f14pwXFR4WrpbVW+rmdjeXeTv9VNGv12VRluPuUK/FV7S+InC+Dw0J1eWtLq9w5+eQ4v0/GIQKb/TC0Rq9cDR/zQ04hqSkpWjguIFKuy/taG8KgMOE6zX+6Oj+WSMAAADgOEDTDQAAAPiMprsSalu7bal4JQCVX3JScqk/0gWg8uN6jT/iM90AAACAz7jTDQAAAPiMphsAAADwWZlzuvf/M6QA3CrLp7aY1yWs/WC9lnFxcc5ar169zHVu3rzZWSssdP8ludBQ+15JUZH7j9uEhYUFtc5atWqZ6/zmm2+cta1bt5rLVibMa+DYcyTnNXe6AQAAAJ/RdAMAAAA+o+kGAAAAfEbTDQAAAPiMphsAAADwGU03AAAA4LMyRwYCwLHKiuGzovRq1qzprHXt2tVc59q1a501K8LKigT0Wtaq5eTkOGvW85Ts+MNjKTIQAMqDO90AAACAz2i6AQAAAJ/RdAMAAAA+o+kGAAAAfEbTDQAAAPiMphsAAADwGU03AAAA4DNyugEc96wsbsuaNWuctWnTppnLbtq0yVmLjIx01kJCQsxxrXpiYmJQy+Xn55vr9MoOBwBwpxsAAADwHU03AAAA4DOabgAAAMBnNN0AAACAz2i6AQAAAJ/RdAMAAAA+IzIQwDHv5JNPNusPP/yws7ZhwwZnrU6dOs5a7dq1zXVmZGQ4a1FRUc5aWFiYOa4V/Tdq1ChzWRevSMDY2NigxgWA4wl3ugEAAACf0XQDAAAAPqPpBgAAAHxG0w0AAAD4jKYbAAAA8BlNNwAAAOAzIgMBHPMuv/xys37FFVc4azt37gxqnXFxcWY9OzvbWbNiAXft2mWO27hxY2dt7Nixzlp6erqzFh8fb66zShUuJQDghTvdAAAAgM9ougEAAACf0XQDAAAAPqPpBgAAAHxG0w0AAAD4jKYbAAAA8Bk5T5VASEhIULWioiI/Nkehoe7f1SIiIsxl9+7de7g3x9M555zjrH3zzTdHcEtwtFStWtWsZ2RkOGuZmZlBrXPHjh1mvbCw0FkrLi4OqibZ21urVi1nbcOGDc6ata2Sf+caADiWcKcbAAAA8BlNNwAAAOAzmm4AAADAZzTdAAAAgM9ougEAAACf0XQDAAAAPqPpBgAAAHxGTncFYGVtS8Fn9lapYr+8VvautWx+fr6z5lcO90UXXWTWb7nlFmetU6dOztpNN93krP3vf/8z1xkeHm7WUXHUqVMn6GWtDOqYmBhnLScnxxzXmmPWOcFrXGt74+PjnTVr7nqdo45G/j6A8omMjDTrubm5QY3rdb7wQ1hYmFkvKCg4Qlti4043AAAA4DOabgAAAMBnNN0AAACAz2i6AQAAAJ/RdAMAAAA+o+kGAAAAfEZk4CEKDXX/nmJFdVnxYOWJsklISHDWdu3aFfS4ViygFTvWuHFjc1xrP3zyySdBrVOSMjMznbUdO3Y4ay+//LKzdsYZZ5jrzMrKMuuoOKx5K9lz14rWtOaJFScoSXl5eWbdxSueLyIiwlnziggL1p49e3wZF0CJYHsPy5dffmnW3333XWdtzJgxzpoVZeyXihIJ6IU73QAAAIDPaLoBAAAAn9F0AwAAAD6j6QYAAAB8RtMNAAAA+IymGwAAAPAZkYGH6GjEAr744ovO2iWXXOKsXXvttea4ixYtctZuvPFGZ+3mm2921jp16mSu87XXXnPWrNi/VatWmePWqVPHWbPiBidNmuSsEQl47PCKsLLmp7WsFfsXFRVlrjMsLMxZs84z0dHR5rhWxGFOTk5Q67S2VZKys7PNOgApJCQk6GWDjQUcP368s3bqqaeay953333O2rx585y1nTt3muPGxsY6ayeddJKzdtlllzlrXvtn8ODBZv1I4U43AAAA4DOabgAAAMBnNN0AAACAz2i6AQAAAJ/RdAMAAAA+o+kGAAAAfEbTDQAAAPiMnO7DKNgs7nvuucesd+7c2VlLTU111r777jtz3FdeecVZe+ihh4Ia18q9lqQGDRo4a8uWLXPW2rdvb44bGur+/fHSSy911pYuXWqOi2ODV460lbG/fft2Z61evXrOWmRkpLlOK8c7IyPDWfN6Lnv27HHWrFxxi1fO+e7du4MaFzieeM0jP8Z98803nbX09HRz3PPPP99ZmzNnjrOWn59vjrt3715nzeqjrHPquHHjzHVWFNzpBgAAAHxG0w0AAAD4jKYbAAAA8BlNNwAAAOAzmm4AAADAZzTdAAAAgM+IDDxEVjRdUVGRs9a3b19n7brrrjPXmZaW5qzVqFHDWVu5cqU57oABA5y1Z555xlm75ZZbnLX169eb67QiA61lP/roI3PcF154wazj+Pbbb7+ZdSuKyprz8fHxztrUqVPNdZ599tnOWkREhLMWFhZmjhsSEuKs7dq1y1mznqfXOjMzM806AFuzZs3MuhXVO2bMGGfNmvOtWrUy12nN+23btjlrhYWF5ri5ublB1axxExMTzXVWFNzpBgAAAHxG0w0AAAD4jKYbAAAA8BlNNwAAAOAzmm4AAADAZzTdAAAAgM+IDNyPFdUlSXl5ec6aFfnzyiuvOGvz588319mwYUOz7rJixYqgxz3vvPOctU8++cRZmzRpkrnOGTNmmHXAD+np6Wbdigy0zglWbc2aNeY6mzdv7qwlJyc7a1ZUl2THamVnZztrVjyYFYfqNS5QEVnRmsXFxUGPa82jBQsWOGvh4eHmuNa8/+qrr5y1iy++2Fm76KKLzHV6RQC7eEWMWvXo6GhnLT8/31k74YQTvDesAuBONwAAAOAzmm4AAADAZzTdAAAAgM9ougEAAACf0XQDAAAAPqPpBgAAAHxWaSMDvSJpQkPdv09YkVpWJKCXVatWOWtvvfWWs3brrbea4+7cudNZq127trO2YcMGc9y9e/c6a+3atXPWzjzzTGetevXq5jqDjQxs27atWW/cuLGzdvbZZztrJ510krPWpEkTc51erxsqDmtuSlKVKu5TYUFBgbNmRYvt2bPHXGdWVpazZp3frPOXJOXm5jprOTk5zpoVWea1Tq86ECzrWu4V7WfVg40FvOSSS8z6Rx995KxZ56Fdu3aZ444dO9ZZe/DBB501K0rPq0ew9pEV32f1FpJ9rrHiSa1zZs2aNc11VhTc6QYAAAB8RtMNAAAA+IymGwAAAPAZTTcAAADgM5puAAAAwGc03QAAAIDPaLoBAAAAn1XonO6QkBBnza/c2NjYWLPulb3rMmzYMGfNytGUpIcffthZW716tbPWu3dvc1wr/3vlypXOmpVb/Kc//clcZ/fu3Z01K2czKirKHNfKV1+zZo2zZj0XK0tUsrPBUbFY80Syc7FjYmKcNSvfOzMz01zn5s2bnbWIiAhnzetvFFh5v1aGd2RkpLNmZfKicrGuq5J9fFnLWvnKXpnY1jr9Ovasv3Fh/V0Nr/P+ggULnLV169Y5az/++KM5buvWrZ01qy+x9r1Xn2RdH61eKTEx0Rx3/fr1zpp1TrWOk9NOO81c54UXXmjWjxTudAMAAAA+o+kGAAAAfEbTDQAAAPiMphsAAADwGU03AAAA4DOabgAAAMBnZY4MtKJaQkOD792tSBor6sYrkuaCCy5w1qzIn4EDB5rjzpkzx1m79dZbzWVdHnnkEbOek5PjrD3xxBPO2k8//WSOa0XzWDFpVrTYDz/8YK7TGjcjI8NZ84pqDDYi0ooFrFu3rrnshg0bglonjjyvyEDrPGRFoVm1vXv3muvcvXu3s2ZFs3mdb63zhfU8rXG9It9QeXi9ltYx4hdrHlm8YuCs6/m1117rrH333XfO2m+//Wau07oG1qpVy1m7/vrrzXGbNm3qrO3YscNZ2759u7NmXcslOxZwyZIlztqyZcvMcfv16+esWfHASUlJzppXxO8111xj1o8U7nQDAAAAPqPpBgAAAHxG0w0AAAD4jKYbAAAA8BlNNwAAAOAzmm4AAADAZ2WODLQi2YKNayuPYcOGmXUrYm7t2rXO2tdff22Oe9dddzlrwUYGehkyZIizdsIJJzhrN954ozluamqqs5afn++sbdq0yVmzIoYkKTc311mzYtK8oo2Cja3Mzs521iIiIsxlrX2EisXrHGVFbllxqeWJDLSOH2ueWHNekr799ltnzYopjI+PN8fF8cE6h1txbjt37nTWvGII4+LinLURI0Y4a3/605/McWfMmOGsvfTSS86atb1ez6VJkybOmhVlvGvXLnPc9PR0Zy0vL89Zs15P65rrVa9WrZqzdvrpp5vjtmjRwlmzzovW9drrfNupUyezfqRwpxsAAADwGU03AAAA4DOabgAAAMBnNN0AAACAz2i6AQAAAJ/RdAMAAAA+o+kGAAAAfFbmnO769es7a1YupST98ssvztrmzZudteLiYmetWbNm5jotXbp0cdbKk1XbsGFDZ239+vVBj2tlkg8aNMhZW7hwoTmulV1cr149Z61Dhw7OmvV6StLWrVudNStn08pKluznYh1HFq/ljkY+PfyRmZnprIWHhztrVgaudaxLdraudbxb2yPZf4fAyhi2svC9solRebz33ntmvXbt2s6a9fcvrGO2UaNG5jqTkpKcte+++85Zu//++81xrWPa6iFq1KjhrDVu3NhcZ0JCgrOWkZHhrFmZ/5K9f63naY3rtc6cnBxnrX379s6aVx9lnW+tc411TfbKHK8o12vudAMAAAA+o+kGAAAAfEbTDQAAAPiMphsAAADwGU03AAAA4DOabgAAAMBnZY4MvPzyy521m266yVw2KirKWbOi9CZMmOCsWZF2ktSqVStn7ddff3XWvKLprG06/fTTnbW//OUvztq1115rrtPy888/O2txcXHmsm3btnXW1qxZ46z179/fWZs5c6a5Tiv+KTc311nziizzigvyg1fcEiqPnTt3OmuJiYnOmnVc/vbbb0FvT5Uq7lNzdna2uawVvWltr7VOa0xUPH379nXWvK6dVpxbTEyMs2bFuaWnp5vr/PHHH501K1qzZcuW5rhW9J9VsyLvIiIizHXu3r3brAfLj8g7r2uYVbfiI72ux6Gh7vu9Vr9o7YOj9bocKu50AwAAAD6j6QYAAAB8RtMNAAAA+IymGwAAAPAZTTcAAADgM5puAAAAwGdljgxcuHChs+YVYWXVa9as6azde++9ztr27dvNdf7000/OmhVnY0XZSHYU4VtvvRXUuL/88ou5TiuuKykpyVmzonckqXfv3s7axIkTzWWDVb16dWfNio/0igOyWFFWwdYk7xhDVB7Wa2nFVFmRWlb0mmTHFHqdhyxW9F+wkYEc65XLjh07nDXrmiHZUXA5OTnOmnX8eB3PDRo0cNaio6OdNa/jsmrVqs7aCSec4KxZ11yva5FVt/aRV3yfdT0KNr7W6xpnxTXm5+c7a17xhl7RzC7lOd9afdbZZ58d1PYEgzvdAAAAgM9ougEAAACf0XQDAAAAPqPpBgAAAHxG0w0AAAD4jKYbAAAA8FmZIwOtSJ+4uDhz2aysLGfNiiAKNp5IknJzc521yMjIoJbz2qZ169Y5a1Z8X3lij6ZPn+6s3XPPPea4frD2rWRHCVmvqRXzKNmvW7BRVl6vCzFqxw4rlsxiRVhZkYCStHv3bmct2JhCyY4ss87F1jnKOu+h4klJSXHWfvjhB3NZKxY3ISHBWQv2Oi/Z528rHtgritCKtUtPT3fWrGuGV2Sg9Vysa4ZXfJ/FOl9Y8XxefZS1vcHGrHrVrfOb9XqGh4eb6/TqIY4U7nQDAAAAPqPpBgAAAHxG0w0AAAD4jKYbAAAA8BlNNwAAAOAzmm4AAADAZzTdAAAAgM/KnNM9depUZ+3RRx81l61Tp46ztnXrVmfNyqe2MkElO0vTypf0yv20sh6t7bWyJ63lJKlWrVrO2tlnn20ua7FyLYPNE/XKOf/pp5+cNSvvPS8vzxy3Zs2azpqV82rlfm7YsMFcp9exgspjz549zpqV4W2dD7yyardt2+asWedFr5xga65Yx3tMTIyztnfvXnOdqDxuv/32oJe9+uqrnbWbbrrJWTv55JPNca05Zl3rd+3aZY5rZVRby1rXRq/8fSvv3qpZ2yrZmdrWstb5wq/saq9zlLW91nnT6j28/kbIF198YdaPFLoGAAAAwGc03QAAAIDPaLoBAAAAn9F0AwAAAD6j6QYAAAB8RtMNAAAA+KzMkYFWvNUpp5wS9AZcc801zlrHjh2dtR49epjj5uTkOGudOnVy1qyoLsmONsrMzAyq9txzz5nrnDhxorNmxRdZsUeSHR9mxRNZcYJeUUHnnHOOs/af//zHWbvyyivNcb/88ktnrVevXs5aamqqs+YVcxUbG2vWUXlY5zcrjrI8kVtWlKUVMeoVLbZ7925nzZq71rhEBkKSPvnkk6BqXk4//XRnrVWrVs5aw4YNzXETEhKcNetabsVnel3jrNhcK/7QK27XijW15qcVjeh1/rLi+6zIXGtbJfu5WrGAVr9jnfckafbs2c7aLbfcYi57OHGnGwAAAPAZTTcAAADgM5puAAAAwGc03QAAAIDPaLoBAAAAn9F0AwAAAD4rc2SgFQ9jxVt5GTNmTFC1Bx98MOh11qlTx1nbsWOHuWzdunWdtTVr1gS9TX6wIgG9WLE9lry8PLN+7rnnOmspKSnOWocOHcxxf/zxR2etadOmzlp8fLyzZsU8SlJaWppZR+WxfPlyZ82KLvWK77NkZ2cHvaxl48aNzpoVAWbxijMDymPu3LlB1YDKhjvdAAAAgM9ougEAAACf0XQDAAAAPqPpBgAAAHxG0w0AAAD4jKYbAAAA8BlNNwAAAOCzMud0W1ncISEh5rJWvTwZ38FKT08Pelk/sritDHSvekFBQdDrtV6XYPN8vVhZ3BYrh9vL6tWrg14Wx4fZs2c7a3/605+ctWXLlgW9Tq9Mexev88WKFSuctSpV3Kf8Ro0aOWuxsbHeGwYAMHGnGwAAAPAZTTcAAADgM5puAAAAwGc03QAAAIDPaLoBAAAAn9F0AwAAAD4rc2Sgpbi4uFz1451XbKJfsYq8LkCJ5cuXO2vW/CvPHJo3b56ztnfvXmctPDzcHHf79u3O2qZNm5y1d99911n75ZdfzHUCALxxpxsAAADwGU03AAAA4DOabgAAAMBnNN0AAACAz2i6AQAAAJ/RdAMAAAA+OyyRgQBQmf3666/O2p49e5w1v+I8s7OznbW4uDhz2by8vKDWuXjx4qCWAwCUDXe6AQAAAJ/RdAMAAAA+o+kGAAAAfEbTDQAAAPiMphsAAADwGU03AAAA4DMiAwHAkJ+f76wlJCT4sk4rijA+Pt5cNicnJ6h1VqnivhwUFBQENSYA4Hfc6QYAAAB8RtMNAAAA+IymGwAAAPAZTTcAAADgM5puAAAAwGc03QAAAIDPaLoBAAAAn5HTDQCGSZMmOWuNGzf2ZZ1jxoxx1lq2bGkuG2xOd2FhYVDLAQDKhjvdAAAAgM9ougEAAACf0XQDAAAAPqPpBgAAAHxG0w0AAAD4jKYbAAAA8FlIcXFx8dHeCAAAAOBYxp1uAAAAwGc03QAAAIDPaLoBAAAAn9F0AwAAAD6j6QYAAAB8RtMNAAAA+IymGwAAAPAZTTcAAADgM5puAAAAwGc03QAAAIDPaLoBAAAAn9F0AwAAAD6j6QYAAAB8RtMNAAAA+IymGwAAAPAZTTcAAADgM5puAAAAwGc03QAAAIDPaLoBAAAAn9F0AwAAAD6j6QYAAAB8dlw13QPHDdRlYy472ptRbkNShmjguIFHezMklWxL27faHu3NwDHuWJm7luRXk5WSlnK0N0NSyba8OvfVo70ZOAKO9twqyzWk2+huum/KfUdkew63lLQUJb+afLQ3Q1LJtoQMDVHm3syjvSkBZdmmY6nPqHK0N2DguIF6b9F7kqTw0HA1TGyoAW0G6PEuj6tK6FHfPEnSpqxNeu6b5zRx5URt3L1RNWNrqm3ttrrvtPt0XpPzDtt6kl9N1n2n36f7Tr8v6DFS0lJ07nvnmo+ZccMMdUvudshjhwwN0edXf67LWl4W3MZ5qEz7GRV/7v5x+6qEVlHV6Ko6tdapuvbkazWw7UCFhlSeew5/fC4H0yixkdLuSzvkcUcvHK37ptynzEczg984Q8jQkMD/x4THqG58XZ3V4Czd3fludajbwZd1Hgsq8tz642t6ME91fUpDug05rOsce/VYhYeGm49Jy0xT49ca66fbflLb2m0PqA9NGaqV21fqw8s/9P1adij82p/dRndT29pt9WrPV4PbMGPcmetmOutdG3VVysCUw7rOB898UHd3vtvzcda1fWbaTP3p8z9pw583+LZvyuLoXxkl9WzWU6P6jFJuQa4mrZykOyfdqfDQcD3W5bEDHptXmKeIsIgjtm1pmWk6692zlBSVpL9e8FedUusU5Rfma+rqqbpz0p1aftfyI7YtZXFmgzOV/kB64N/3TrlXu3J3aVSfUYGfVY2uGvj/I70/XSrbfkaJijx3/7h9hUWF2rxns6asmqJ7p9yr/y77r7649gtnA5NfmK/wMPsifyS91vM1DTt/WODfdV6uo1F9Rqlns56SpLCQsFKPryjzWlJgO/cW7NUvGb/o7R/f1mkjT9O7fd7VgDYDDrpMYVGhQkJCKtUvRodbRZ1bf7y+fPLzJ3oy5UmtuGtF4GdxEXGHfZ1/vGYdTF5hnucY41eM16NnP3q4NumwOZT9WVxcrMLiwqP6i9fYq8cG9veGnRvUeWRnfXX9Vzqp5kmS5MtxGBcRZx5XZTn+x68Yr0tOvORwb9ohqxBntMiwSNWOq61GSY00uNNgnd/kfH3xyxeSfn/r67lvnlPdl+uqxd9bSCp5sa/6z1VKGpakqi9WVZ8xfZSWmRYYs7CoUPdPvV9Jw5JU7aVqenjawypW8SFv2x0T71CIQjTv5nnq17qfTqx2ok6qeZLuP+N+zb15buBx63euV58xfRT3fJwSXkjQVf+5SpuzNgfqq7evVp8xfVRreC3FPR+nTu900ldrvgrUu43upnU71+nPU/+skKEhnr/9ukSERah2XO3Af9FVogP7t3Zcbb31w1vq/E5njVwwUo1fa6yoZ6MkHfzt5LZvtdWQlCGBuiT1/aSvQoaGHPB22QeLPlDyq8lKHJaoa/57jXbn7j6k7a5s+xklKvLc/eP21Uuop/Z12uvxLo9r/DXjNXnVZI1eODrwuJChIRoxf4Qu/fhSxT4fq+dmPSdJGr98vNr/s72ino1Sk9eaaGjKUBUUFUgquQAOSRmihq80VOSzkar7cl3dM/mewJhvzn9Tzd9orqhno1RreC1d8ekVQT0HSUqMSiw1ryUpKSop8O9O73TSMzOf0YDPByjhhQTd+uWtB33bduGmhQoZGqK0zDSlpKXoxvE3amfuzsBc2DffJSk7P1uDxg9S/AvxavhKQ73949tBbfu+7UxOStaFTS/Uf6/6r/qf2l93TbpLO3J2SCq54540LElfrPhCrf/RWpHPRmr9zvXKLcjVg/97UPX+Vk+xz8fqtJGnlfoIzrrMdbrk40t0wosnKPb5WJ305kmatHKSJGlHzg71H9tfNf5aQ9HPRav5G8016qdRB9vECqmizq0/HoeJUYkKUUipnx2sOUpJS1Hndzor9vlYJQ1L0lnvnqV1metKPca6huz/8ZLkV5MPON4bv9ZYktTun+0UMjRE3UZ3Czx+w84NWrp1qXo262ley0bMH6GmrzdVxDMRavH3Fvpg0QeltnHfeeKif1+k6Oei1eS1Jvrvsv8e0v7bn7U/l29brvgX4jV55WR1eLuDIp+N1Oz1sw/6kaD7ptwXeM4Dxw3UzHUz9dr3rwXm9h+Pgx9/+1Ed3+6omOdidOa/ztSKbStUVlWjqwa2r0ZsDUlStZhqgZ8d7Bcka56WZZv2/3jJwY5/r2v7Fyu+0KUtLjX3zcy0mer8TmdFPhupOi/X0aNfPRo430slx+Fdk+7SXZPuUuKwRFV/qbqe+PoJFReXfQ5ViKZ7f9Hh0aV+c52+drpWZKzQtOunacK1E5RfmK8eH/ZQfES8Zt04S3MGzVFcRJx6ftgzsNzL372s0QtH690+72r2jbO1PWe7Pk/9vNR6Ri8cbTZd23O2a8qqKbqz052KjYg9oJ4UlSRJKiouUp8xfbQ9Z7tmDpypaddP05oda3T1f68OPDYrL0u9mvXS9AHT9dNtP6ln05665ONLtH7nekklvz3WT6ivp7s9rfQH0kv99nu4rdq+Sp+lfqaxV43VwtsXlmmZ+bfMl1Ry1yr9gfTAvyVp9Y7VGrdinCZcN0ETrp2gmetmatjs3+/KHa/7+XhUUeaupXvj7mpTq43Gpo4t9fMhM4eob8u+WjJ4iQa1G6RZ62ZpwLgBuve0e7XszmX6Z+9/avSi0Xrum5KG/LPUz/TK3Ff0z97/1Mq7V2rcNeN0Ss1TJEk//PaD7pl8j57u9rRW3LVCU/pP0TmNzglqe8tq+HfD1aZWG/1020964pwnPB9/ZoMz9WqPV5UQmRCYCw+e+WCg/vJ3L6tj3Y766bafdEenOzR44uBSF8Juo7sF/d2SP5/+Z+3O261pa6YFfpadn60X57yokZeO1NI7lqpmbE3dNekufffrdxrTb4wW375YV7a+Uj0/7KmVGSslSXdOulO5Bbn6ZuA3WjJ4iV48/8VA0/fEjCe0bOsyTe4/Wal3pmrExSNUPaZ6UNtbEVSGuXUwBUUFumzMZeraqKsW375Y3930nW5tf6tCQn5fh9c15GD2P97n3TxPkvTV9V8p/YF0jb369/n9xYov1C25mxIiE5zXss9TP9e9U+7VA2c8oJ/v+Fm3dbhNN46/UTPWzii13idmPKF+rfpp0e2L1P+U/rrmv9codWvqYdlXLo9Of1TDzhum1DtTdWqtUz0f/1rP13RG/TN0S/tbAnO7QUKDQP3/vv4/vXzhy/rh1h9UJbSKBn0xKFBLy0xTyNCQw/r9EmuelmWbDmb/49+6ti/dslRb9mxR98bdnftm466N6vVRL3Wq20mLbl+kEReP0L9++pee/ebZUut9b9F7qhJaRfNunqfXer6mv839m0YuGFnmfVEhPl6yT3Fxsaavna6pq6aW+vxObHisRl46MvD2wYeLP1RRcZFGXjoyMHFH9RmlpGFJSklL0YVNL9Src1/VY2c/pstbXS5Jeqv3W5q6emqp9SVGJqpFtRbO7Vm1fZWKVayW1Vua2z19zXQt2bxEa+9dqwaJJQf2+33f10lvnqT5G+erU71OalO7jdrUbhNY5pnuz+jz5Z/rixVf6K7Od6lqdFWFhYQpPjI+cCfLL3mFeXr/svcDv6WWxb7H7rtr9UdFxUUa3We04iPjJUnXn3q9pq+drudU0pwcr/v5eFLR5q6XltVbavHmxaV+dt3J1+nGdjcG/j1o/CA9etajuqHtDZKkJic00TPnPqOHpz2sp7o9pfU716t2XG2d3+R8hYeVfO62c73OkkrekYmNiFXvE3srPjJejZIaqV2ddkFvb1l0b9xdD5z5QODfG3ZtMB8fERZR6s7a/no176U7Ot0hSXrkrEf0ytxXNCNthlpUL9nvDRMbqk5cnaC2dd9c/+Pdt/yifL3Z683A/F2/c71GLRyl9X9er7rxdSWVfLZzyqopGrVwlJ4/73mt37le/Vr10ym1Sn7ZaXJCk8B463euV7va7dSxbkdJUnJSclDberRVtrm1v125u7Qzd6d6n9hbTas2lSS1qtGq1GO8riEHs//xHpZZ8hGrfXdd/2j8ivHq06KPJPe1bPh3wzWw7cDAMX//Gfdr7q9zNfy74Tq38e/fk7qy9ZW6uf3NkkquL9PWTNMb897Qmxe/eQh75dA83e1pXdD0gjI/PjEqURFhEYoJjzno3H6u+3PqmtxVkvTo2Y/q4o8u1t6CvYqqEqXw0HC1qNZCMeExh237rXlalm06mP2Pf0nOa/v4FePVo1kPRYRFBP7bf9+8Of9NNUhooL/3+rtCQkLUsnpL/bb7Nz3y1SN6suuTgY+6NUhooFd6vKKQkBC1qN5CS7Ys0StzX9EtHW4p076oEE33hF8mKO75OOUX5auouEjXnXJdqS8OnFLrlFI7dtGmRVq1fZXiX4gvNc7egr1avX21dtbbqfSsdJ1W/7RArUpoFXWs27HU2wB9W/VV31Z9ndtV1rcMUrelqkFig0AjKEmta7RWUlSSUrelqlO9TsrKy9KQlCGauHKi0nenq6CoQDkFOYE7sEdSo6RGh9Rwe0lOSg6cLCWpTlwdbdmzJfDv43U/Hw8q6tz1UqziUnfaJAWas8C2bl6kORvmBD5qIkmFxYXaW7BX2fnZurL1lXp17qtq8noT9WzaU72a99IlLS5RldAquqDJBWqU2Kik1qynejbtqb6t+h7WC9n+Otbp6P2gQ3Bqzd/vqIWElDTmf5zX7/d9P+ix972WIfr9NYgIiyh1F2/J5iUqLC7UiW+cWGrZ3MJcVYupJkm657R7NHjiYP1vzf90fuPz1a91v8AYgzsOVr9P+2lB+gJd2PRCXdbyMp3Z4Mygt/lIq4xza/3O9Wr9j9aBfz/e5XE93uVxDWw7UD0+7KELml6g8xufr6tOukp14n//hc3rGnIwZT3ed+Xu0sx1M/WvS/9lPi51a6pubX9rqZ+d1eAsvfb9a6V+dkaDM0r/u/4ZWrh5YZm2JVj7n5vK64/zbN8vzlv2bFHDxIaql1CvXN+hOunNkwIfHerSqIsm959sztOybNPB7H/8W8avGK+7Ot1lPiZ1W6rOaHBGqevCWQ3OUlZeln7d9WtgO06vf3qpx5xR/wy9/N3LKiwqVFho2AHj7q9CNN3nNj5XIy4eoYiwCNWNr3vAlwRiw0t/5CArL0sd6nbQvy//9wFj1Yg5fM1k82rNFaIQLd9W/i/xPfi/BzVtzTQNv2C4mlVtpujwaF3x6RVl+gLI4bb//pSk0JDQA5rf/KL8Mo23/7fKQ0JCVFRcVObtOVb38/Ggos5dL6lbU9U4qXGpn+3/0aasvCwN7TY0cFfwj6KqRKlBYgOtuGuFvlrzlaatmaY7Jt2hv377V80cOFPxkfFacNsCpaSl6H+r/6cnU57UkJlDNP+W+YGPSx1u+2//vjszf5zX+YVlm9OSDvgiaYgObV5bUreVvB3f+ITfX4PoKtGlLmZZeVkKCwnTj7f+eMDFbN9b0ze3v1k9mvbQxJUT9b/V/9MLs1/Qyxe+rLtPu1sXNb9I6+5bp0krJ2nammk67/3zdGenOzX8wuGH5Tn4rTLOrbrxdUt9ZHHf53tH9RmlezrfoymrpuiTpZ/oLzP+omnXT9Pp9U+XFNw15GAfRTyYySsnq3WN1qVu1lQ2B5vb+38WP9i5vW/OHa65Pem6SYHeIbpKtCR7nga7TQfrYw4mfXe6fkr/SRefePEhPxc/VIjPdMeGx6pZ1WZqmNiwTN/KbV+nvVZmrFTN2JpqVrVZqf8SoxKVGJWoOnF19P2v3weWKSgq0I+//XhI21U1uqp6NOuhf8z/h/bk7Tmgvu8LSq2qt9KGnRu0Yefvb+cu27pMmXsz1bpGyW/9czbM0cA2A9W3VV+dUusU1Y6rXeqtVankTk9hUeEhbePhUiO2htKzfv8M1K7cXVq7Y22px4SHhvuyfcfTfj7WVNS5a/l67ddasmWJ+rXq57mtK7atOGA7m1VtFmhoo8OjdUmLS/T6Ra8r5YYUfffrd1qyZYmkkruI5zc5Xy9d8JIW375YaZlp+nrt14fteXjZ12j9cV4v3LSw1GMiwiJUWHzk58Krc0s+S35+k/Odj2lXp50Kiwu1Zc+WA/b/H98WbpDYQLd3vF1jrx6rB854QO8seCdQqxFbQze0vUEfXv6hXu3xatBfBj0aKuPcqhJapdR6//ilunZ12umxLo/p25u+1ck1T9ZHSz46bOuVfk/N2P/c/sePluxzsGtZqxqtNGfDnFI/m7NhTuDass/cX+eW/vfGuWpVvfTHZfxWI6aG0neX/j7S/nfbj9Z1rlFSo8DrXy+hXuDn1jw9XA72nL/85Uud2eDMUsfiwR7Xqnorfbfhu1I3KeZsmKP4iHjVT6gf+Nn3G78vtdzcX+eqedXmZbrLLVWQpvtQ9T+1v6rHVFefMX00a90srd2xVilpKbpn8j36ddevkqR7T7tXw+YM07jl47R823LdMfGOA8LXP0/9XC3/bn+O+B+9/qHC4kJ1HtlZny37TCszVip1a6pe//51nfGvkreZzm9yvk6pdYr6j+2vBekLNG/jPA34fIC6NuoaeFuoedXmGrt8rBZuWqhFmxbpus+uO+C3uOSkZH2z/htt3LVR27K3Haa9VTbdk7vrg8UfaNa6WVqyeYluGHfDAQdRclKypq+drk1ZmwKpA2XBfsY+R3LuSiUfRdiUtUkbd23UgvQFen7W8+ozpo96n9jbGVe3z5PnPKn3F7+voSlDtXTLUqVuTdWYn8foL1//RVLJF87+teBf+nnLz1qzY40+XPyhoqtEq1FiI034ZYJe//51Ldy0UOsy1+n9Re+rqLjosH5W1kuzqs3UIKGBhqQM0cqMlZr4y0S9/N3LpR6TnJSsrLwsTV8zXduytyk7P7vM4w/4fIAe++rA+Lr9Ze7N1KasTVqXuU7TVk/TFZ9eoY+WfKQRF48w7/qfWO1E9T+lvwaMG6CxqWO1dsdazds4Ty/MekETf5koqSSxYeqqqVq7Y60WpC/QjLQZgc8LPznjSY1fPl6rtq/S0i1LNWHlhAM+S3wsOdJzq6zW7lirx756TN9t+E7rMtfpf6v/p5UZKw97o1oztqaiq0Rryqop2py1WTv37lRBUYEmr5qsS1tcWuqxB7uWPXTmQxq9cLRGzB+hlRkr9bfv/qaxqWNLfblYkv6z7D9696d39UvGL3pqxlOat3Ge7upsf3ThcOveuLt++O0Hvb/ofa3MWKmnZjyln7f8XOoxyUnJ+n7j90rLTNO27G1lvpO9cddGtfx7S83bOO+wba81Tw+ng13b96WW7P+4/ffNHZ3u0IZdG3T35Lu1fNtyjV8+Xk+lPKX7z7i/VHTp+p3rdf/U+7Vi2wp9vORjvTHvDd172r1l3sYK8fGSQxUTHqNvbvxGj3z1iC7/9HLtzt2tegn1dF7j85QQmSBJeuDMB5Sela4bxt2g0JBQDWo7SH1b9dXOvTsD4+zM3akVGXZUTpMTmmjBrQv03Kzn9MD/SsasEVNDHep20IiLR0gqeStk/DXjdffku3XOqHMUGhKqns166o2L3giM87cef9Og8YN05r/OVPWY6nrkrEe0K3dXqXU9fe7Tum3CbWr6elPlFuaq+KngYtKC8ViXx7Q2c616f9xbiZGJeubcZw640/3yhS/r/v/dr3cWvKN68fXK/Mc42M/Y50jOXUmasmqK6rxcR1VCq+iEqBPUpnYbvd7zdd3Q9gbPDOgezXpowrUT9PQ3T+vFOS8qPCxcLau31M3tSr5ElRSVpGGzh+n+/92vwqJCnVLrFH157ZeqFlNNSVFJGps6VkNShmhvwV41r9ZcH/f7OJBleySEh4Xr434fa/DEwTr1rVPVqW4nPdv9WV35nysDjzmzwZm6vcPtuvq/VysjJ+OQ/hDH+p3ry5SjfeP4ki+nRlWJUr34ejq74dmad8s8ta/T3nPZUX1G6dlvntUD/3tAG3dtVPWY6jq9/unqfWJvSSV3Ne+cdKd+3fWrEiIT1LNZT73S4xVJJXezHpv+mNIy0xQdHq0uDbtoTL8xZXpuldGRnluHsl3LM5brvU/fU0ZOhurE1dGdne7UbR1vO2zrkErusr9+0et6eubTejLlSXVp2EVPnPOE4iLiDjjWDnYtu6zlZXqt52sa/t1w3TvlXjU+obFG9Rl1wB+SG9ptqMb8PEZ3TLxDdeLr6ON+Hx9wN9xvPZr10BPnPKGHpz2svQV7NajdIA04dUDgXTap5EvHN4y7Qa3/0Vo5BTlae+9aY8Tf5Rfla0XGikP6BdyLNU8Pp/2v7VmPZWn62ukH/BGcg+2b5KRkTbpukh6a9pDavNVGVaOr6qZ2N+kv5/yl1LIDTh2gnPwcdR7ZWWEhYbr3tHt1a4fS3wWwhBQfSsAgKoQhKUOUlpmm0ZeNPtqbAuAwSX41WaMvGx3UX4sFcKB7Jt+jgqKCw5YsEsxfskxJS9HAcQOD+ouxKJ+xqWP1l6//omV3Ljss4x2Ov2RZKe90AwAAWE6uebLOqH+G9wNxTIqLiNOL5794tDejFJpuAABwzDmUt/1x7Lmw6YVHexMOQNNdCXVL7nbAl18AVG73nX5fpf0DLsDxIJjv/yQnJeu+0+87/BuDIy5lYEq5x+Az3QAAAIDPKmVkIAAAAFCZ0HQDAAAAPqPpBgAAAHxW5i9ShoSE+LkdFUZYmP2nPAsLg/uzqiNGjHDWTjrJ/oMZ2dnukHqrtmvXLmdNkjIzM521adOmOWsTJ040x7VYx9Gx9PWCyvJcjpd57SU01H3/oaiobH/J7VANHDjQWcvPz3fW9u7da46bnJzsrL388svOmsXaP1782n9HA/P6+NCvXz9n7cQTTzSXzcnJCWqdZ5xhRxvOmDHDWXvrrbeCWidKHMl5zZ1uAAAAwGc03QAAAIDPaLoBAAAAn9F0AwAAAD6j6QYAAAB8Vua/SMm3ob29+eabztptt93mrFkJJJL97f+oqKigx42Li3PWrBSXwYMHO2v//Oc/zXWSXlKxMK/9c99995n1rl27Omu//fabs9auXTtz3PDwcGftb3/7m7P28ccfm+OCeV3RnHrqqWb9sssuc9YuuOACZ62goMBZS0hIMNeZlpbmrDVr1sxZs67lkrR27dqgtslKG5s5c6a5ztmzZ5v1YwXpJQAAAMAxhKYbAAAA8BlNNwAAAOAzmm4AAADAZzTdAAAAgM9ougEAAACf0XQDAAAAPiOn+zCaMmWKs3b66ac7a6tXrzbHbdiwobNm5Wnn5+eb427evNlZq1GjhrO2cuVKZ+2cc84x12kpT4Z3Rcv/Js+3crFy9Pv16+esWVm/77//vrlOK3d34MCBzpqV4e213h49ejhr5557rrP2xhtvmOt8/fXXnbWtW7eay1Ymx/u8tsa1atbfmpCkpk2bOmtPPfWUsxYREWGOa9X37NnjrFmvs3XNlexrZ/Xq1Z21efPmmeNa4uPjnTUrt9/rddm9e7ezdsstt3hvWCVBTjcAAABwDKHpBgAAAHxG0w0AAAD4jKYbAAAA8BlNNwAAAOAzmm4AAADAZ8dlZKAV+VNYWGgue/LJJztr33zzjbOWl5fnrG3ZssVcpxVBtGPHDmetWrVq5rjWemvXru2sWRFEHTt2NNe5atUqZ61KlSrOWkFBgTkukYHBOZbmteWdd94x61deeaWztnPnTmfNOi69jtmEhARnLTTUfT8kOzvbHDc2NtZZs55LZGRkUDVJys3Nddb+9Kc/OWvWObMiYl7746WXXnLWWrVq5axZ8bWSHaVnXetjYmKctaysLHOd1nXXuj7OmjXLHNfa3sTERGctPT3dHNfSsmVLZ23SpEnO2iuvvBL0Oo8GIgMBAACAYwhNNwAAAOAzmm4AAADAZzTdAAAAgM9ougEAAACf0XQDAAAAPnNntB3DvGIBLVb0WFRUlLNmRTiddNJJ5jqtaL+tW7c6a/Xr1zfHbdasmbMWbLTYI488Yq7zlltucda8ItYslSXKC/6Jjo521s4//3xzWStWq6ioyFmz4ketmiTl5OQ4a9a83rt3rzlu48aNnTVrnuzZs8dZs6JJJSkuLs5ZGz16tLPWpEkTc1xULFaUpTVP6tWrZ45rHbPbtm1z1qxoPyn4+Rns3JTsWOEGDRo4a159SUpKirO2fv16Z82KE6xZs6a5zqSkJGetXbt2zlqtWrXMcTdv3mzWj2Xc6QYAAAB8RtMNAAAA+IymGwAAAPAZTTcAAADgM5puAAAAwGc03QAAAIDPKm1koBVdJNnxRdayS5YsMce1InasWK3Y2FhnbdeuXeY6LVbMnlcEkRVjuHv3bmfNivs5/fTTzXX+8ssvztrQoUOdtX//+9/muMCQIUOcNa9oMStKLy8vL6jtKc/8syL44uPjzXGtc4I1r61xq1SxLxVZWVnOWkREhLNWtWpVc9zt27ebdRxZ1nXVct1115l1KwbTOn4yMjLMca24PGvOW3PI2h6vZbOzs50163wgSbVr13bWTjnlFGfNikO14ogl+/W2zm+DBg0yx33hhRfM+rGMO90AAACAz2i6AQAAAJ/RdAMAAAA+o+kGAAAAfEbTDQAAAPiMphsAAADwGU03AAAA4LNKm9MdbF6oJI0bN85Za926tblsZmams2Zl2VoZnDk5OeY6rWWt/GGvfWRlo1qZvdb2WNmnkp0/bGV3zp071xx39erVZh3HvrPPPttZ8zourTxfK4Payt0NCwsz12nl+VrLeuV/h4eHO2s///yzs9ayZUtnzZq3kp23be3bv/71r+a4N910k1lHxWFdM0488URzWSs/vl69es5afn6+Oa51Tbbmn/W3PLyuq1Z2uHWdys3NNcdNSEhw1rp27eqsWeeSn376yVxnZGSks2ZlfDdr1swct3r16s7atm3bzGUrO+50AwAAAD6j6QYAAAB8RtMNAAAA+IymGwAAAPAZTTcAAADgM5puAAAAwGeVNjLQixVr165dO2dt+/bt5rhW/I5XRJiLVxyXFRGWl5fnrJUnJs2KL7Kii6wYIcnev1a8U//+/c1xn376abOOY9+bb77prHXv3t1ctlevXs6aFcFnzTGvaDFrWatmndskO+LQihazziVWdJgkLV261FkbP368szZr1ixzXFQeV1xxhbMWERFhLmtFBlrXm+joaHNcaw5aNetabsWESlLNmjWdtfbt2ztrXrG4//nPf5y1xYsXO2vWddXqASTpqquuctasa71XL3T11Vc7a//4xz/MZSs77nQDAAAAPqPpBgAAAHxG0w0AAAD4jKYbAAAA8BlNNwAAAOAzmm4AAADAZ8dsZGCLFi2ctaSkJGctJycn6HVaMTmhoe7fb6yaJBUUFDhrderUcda8YprK81xdvCKIrChCa9kOHToEvU04Pvz73/8OquYlJSXFWTvppJOctd9++80c14ryslgRopIdKbhjxw5nLSYmJqgxJalnz55mHce+Cy64wFnLyMgwl7ViOa3j3bqeSPY10DqmreW8rtdWFKF1zfV6LgMGDHDWrNhhK0I0Pz/fXOe2bducNWv/WRGQktSsWTOzfizjTjcAAADgM5puAAAAwGc03QAAAIDPaLoBAAAAn9F0AwAAAD6j6QYAAAB8RtMNAAAA+OyYzemuX7++s2ZlgnrlS1qZ2QkJCc6alVO6d+9ec51WTqmV++mVwx0dHR30si5WJqgkxcfHO2tWbnFycnJQ24Nji1detEtxcXHQ61y1apWzZv09AK91Wnm+Vhaw17jW3wuwlrXmn5XXWx7lyTzGkTdw4EBnzbpmeF0XLNY1OTIy0lw2Ly/PWbOuq9ZxV6NGDXOdixYtCqq2Z88ec1zrem09F+ua68V63azt9fobBHXr1nXWHn74YWftpZdeMsetDLjTDQAAAPiMphsAAADwGU03AAAA4DOabgAAAMBnNN0AAACAz2i6AQAAAJ8ds5GBF1xwgbNmxY55RVhZsUhWhI4V4xUbG2uuc/v27c7a/PnznbWOHTua45588snOmhWNaD0Xr4gvK0rI2rf16tUzx8XxIdjoP+uYlezILSvu01KeODNrnnidoyz5+flBrXPGjBlBr9NCJGDlUrt2bWfNiqbzusZZc8GKyvM6H1jHdEREhLNm9Qhex6w1x6xxk5KSzHF37doV1LjW/vOKcmzSpImzZr2mXjHIO3fudNasfudYwJ1uAAAAwGc03QAAAIDPaLoBAAAAn9F0AwAAAD6j6QYAAAB8RtMNAAAA+OyYjQxs1KhRUMtZcT+SHYWzZcsWZ61OnTpBjSlJzZs3d9asODOvmL3s7GxnzdoPVrxaTExM0Ou0Yt22bdtmjgtYgo0alKRNmzY5a1bsmBcr+i/Ympfw8PCgxp07d27Q67TmtXUuQcUzbNiwoJY7/fTTzbp1vb766qudNa9YTisSz4o4tMbdvXu3uU5rjllxg9a10WtcK67YihOsXr26uc6lS5c6a59++qmztmbNGnNcKx74WMedbgAAAMBnNN0AAACAz2i6AQAAAJ/RdAMAAAA+o+kGAAAAfEbTDQAAAPjsmI0MtCL6rAgdrzguKxLPitnLy8sLqibZcUDlWc6KL8rNzXXWrPi1KlXsQ8qKPbJER0ebdet18YpiAiyZmZnOmhWH53UuCXYuWOcvyZ6f1rLWcl5RqoDFK3LSqltRvA8//LA57rJly5w16/pXUFDgrHld46wIYCti1DqXeImKinLWgo0JlaTJkyc7a1acINy40w0AAAD4jKYbAAAA8BlNNwAAAOAzmm4AAADAZzTdAAAAgM9ougEAAACf0XQDAAAAPjtmc7p37drlrFkZnF7Z1oWFhc5a1apVnbXdu3c7a165u9Y6rcxQr2zdhIQEZ83aR8Hmm0pSWlqas9a0aVNnLTIy0hy3YcOGztry5cvNZXHsszKovfz666/OmnW8lyd31yu7P1hWLq81r9PT0/3YHFQyXtcqF69Meut4r127trO2detWc1xre62/7ZCTk2OOa4mLi3PWrOdpZXhLdv63xToPeZ0X69evH9Q6vbLMvfqEYxl3ugEAAACf0XQDAAAAPqPpBgAAAHxG0w0AAAD4jKYbAAAA8BlNNwAAAOCzYzYy0IrtseKLFixYYI5rRRTdeeedzpoVO+YVh2dFeVnPxSveyVrWihu0opY2btxorvMf//iHs/bKK684a16RU7Vq1XLWiAxEeSIDO3To4KxZ88SK+iyPYGPbJHs/WOO2bt3aHPf777931vzaDzjygp1H5TkGrHg5r+2xrp3Z2dnOWrBxupId7Wddx7z2kRXDZ0UclmffH43X+1jHnW4AAADAZzTdAAAAgM9ougEAAACf0XQDAAAAPqPpBgAAAHxG0w0AAAD47JiNDIyNjXXWrDibzMxMc9xFixY5a8FGeZUn2s96LlZckiSFhrp/5/Ja1sUrYujbb7911sLCwoJapyQlJSUFvSyODX4cz5L0wAMPOGu7d+921ryOZytu0IoRtaLOvFjnGutccvvtt5vjjho1KuhtAix5eXnOmjXnpeCPd6tmRQJKdrRfeeIP/Ti/Wdsq2fHAlvJEtB7ruNMNAAAA+IymGwAAAPAZTTcAAADgM5puAAAAwGc03QAAAIDPaLoBAAAAn9F0AwAAAD47ZnO6rZxbKx9306ZN5rhedRcra9QrpzsiIsJZs3I2vcb1yht12bZtm7Nm5RZL0m+//easxcfHO2s7d+40x01ISDDrOPYFm5MvSa1bt3bWrHlizWuvjFvrPFSeTF5rWeu8mJub66xZ+6c8vHKWy5OvjmODdVx6sY4fK0ffmpvW382QpKysLGctLi7OWfM6f1nnGmteW6zeQpISExODGhdu3OkGAAAAfEbTDQAAAPiMphsAAADwGU03AAAA4DOabgAAAMBnNN0AAACAz47ZyECvKBwXr2g6Ky7PYkX7FRcXm8vm5OQ4a1bMkFcEUUFBQVDLlieez+u5BrtcsJFJgCR17tzZWbOixY4Gr5g9izVPsrOznTWv816dOnWctfT0dGetPDGPOD5Yx4jXdSHY48uaY15jWtf68vQBXlGFwfB6LtHR0Yd9ncc77nQDAAAAPqPpBgAAAHxG0w0AAAD4jKYbAAAA8BlNNwAAAOAzmm4AAADAZ8dsZGBUVJSzVlhY6Kxt2rTJHNeK9cnPz3fWioqKnDUruk+S9u7d66zl5uY6a17RYlb0nxW5mJWV5axZ8YaSVKtWLWdt+/btzppXbFtsbKxZx7HPmtdeOnXq5KxZsVrWcWnN+aPFOidY22tFnUlS48aNnTUrMjDYCFFA8o68s453q2ZdV8tzLbLG9bp2Vq9e3Vmzeg+r5oVIz8OPO90AAACAz2i6AQAAAJ/RdAMAAAA+o+kGAAAAfEbTDQAAAPiMphsAAADw2TEbGWhFXFnRWF4xXyeffLKz9ttvvzlr0dHRzppXbJYVKWiN6yU7O9tZCzZy0eu5nHrqqc6atf+Sk5PNcRMTE806YLGOS2v+WecZrwhDK47LqnlFgQY7P60oNK91WufFb7/9NqjtAbx4HZfh4eHOmnXsxcTEOGuZmZnmOq3zhTWu1/nCihu0nqfFa/4RxXv4cacbAAAA8BlNNwAAAOAzmm4AAADAZzTdAAAAgM9ougEAAACf0XQDAAAAPqPpBgAAAHx2zOZ0W5mzVt6llV0tSb169QpqWSuf0ysbPNgMTmsfSHYuqFXbu3evsxYXF2eu84QTTghqXK99VJ68clQeVi6v1zFiOeWUU5y17du3O2uRkZHOmte5xMriLk9mtrUfrHldnn3bpUsXZ+3tt9921sjpPj749TqXZ85b22TVrDkv2f2FNf/Kcw2z/q7Gnj17nDWvc4nVtyA43OkGAAAAfEbTDQAAAPiMphsAAADwGU03AAAA4DOabgAAAMBnNN0AAACAzyptZKBXlI0Vs5eTk+OsJSUlmeO2atXKWbMif6xoo927d5vrtJ5rfn6+s2bFCEl2XJAVk2Ztj1dkYEJCgrMWbISh1zYBXvGZGRkZzpo1d63YPy/lWdZixZ1Z67TOmV7zr3379t4bBgQhIiLCWfOKvLPq1rXTWqcVbStJeXl5zpp1fbSWk4KPG7TmtVfkYmxsrFnHoeNONwAAAOAzmm4AAADAZzTdAAAAgM9ougEAAACf0XQDAAAAPqPpBgAAAHxWaSMD4+PjzXqwUUFt27Y1x61evbqzZsXvZGdnO2tecWbWuFWquF9Crzgla9lg4w/37NljrrNp06ZBjWvFoEnezxXHhmBj9ho3bmzWrWisXbt2BbU9Xtsa7HMpT9RgsOeSgoICc9yGDRsGvU2AxYrv8+J1bXWx4vu85p+1vdZ11SuK0DpHWXPX6ne8okCtuEEEh04FAAAA8BlNNwAAAOAzmm4AAADAZzTdAAAAgM9ougEAAACf0XQDAAAAPqPpBgAAAHxWaXO6vbIyg8183rRpkzmulWtp1azt8crKtDKorRxSr2xdK7/TqlnjeuV6WnnlVjaqV053YmKiWcexwes4cOnatatZt3JuLcFujxT8vPbKHrbOjdZ5yNoer3NURkaGs9asWTNnbdWqVea4ODaUZ55UrVrVWfPqA6y5Yl3jrHG9not1HbOyuL3Gzc3NddYSEhLMZV28/r7Fjh07ghrXS3n2b2XHnW4AAADAZzTdAAAAgM9ougEAAACf0XQDAAAAPqPpBgAAAHxG0w0AAAD4rNJGBnpF5AQbfxUfH2+Oa0UKJiUlOWsRERHOWrBxZVLwEWBerGWtmlfcT2RkpLO2Zs0aZ61NmzbmuI0aNTLrOL6ddNJJZj3Y4708cyzYWECvyECr7hWxFuxyUVFRzlqrVq2cNSIDjw/liYGLi4tz1rzmnzUXrGuRtZzX9To2NjaoZa0ewWubrJ4m2GhSqXy9CQ6OO90AAACAz2i6AQAAAJ/RdAMAAAA+o+kGAAAAfEbTDQAAAPiMphsAAADwWaXNg0lLSzPru3btcta2bNnirC1YsMAc9y9/+YuzZsUJhoeHm+NarMif7OzsoNcZbPRfXl6es2bFJUlSgwYNnLWRI0c6a3379jXH3bZtm1nHscGKyLRYx51kR25Z9u7d66xZ88Rrndbz3LNnjzmuNXcLCgrMZYPZHq91WnGNX375ZVDbg+OHNce85m1ubq6zZh3TWVlZQa/TmvfWsl6xilZ8nzWuFefpJT8/P+hlcXDc6QYAAAB8RtMNAAAA+IymGwAAAPAZTTcAAADgM5puAAAAwGc03QAAAIDPKm1kYHnidWrUqOGsTZs2zRy3ffv2zlqtWrWcNSuez4v1XHbs2BH0OiMiIoLanpycnKBqkh3J+PTTTztriYmJ5rjliUXCsa9du3Zm3ZoL1rFXvXp1Zy3YeEMvXuc+qx4SEhJUbevWreY64+PjnbVLL73UWRs2bJg5LlC7dm1nrUmTJuay6enpzprVB1gRfF4xel5RoS5hYWFm3TpHnXDCCc6atQ+8ziU4/LjTDQAAAPiMphsAAADwGU03AAAA4DOabgAAAMBnNN0AAACAz2i6AQAAAJ/RdAMAAAA+q7Q53V5ZmZ9++mlQy+7Zs8ccd+HChWYdwZs9e7azNnbsWHPZjz/++HBvDo4hXjnd9erVc9aSk5OdtQYNGjhrVnauJFWrVs1Zi46OdtasPG3Jzt7duXOns5adne2seZ0XrZz877//3lwWsEycONFZW7Rokbms9XcsEhISnLXw8HBnrWrVquY6rblrZXh75XuXZ1kX6xwkec/7YB3P+eDc6QYAAAB8RtMNAAAA+IymGwAAAPAZTTcAAADgM5puAAAAwGc03QAAAIDPQoqP5+wWAAAA4AjgTjcAAADgM5puAAAAwGc03QAAAIDPaLoBAAAAn9F0AwAAAD6j6QYAAAB8RtMNAAAA+IymGwAAAPAZTTcAAADgM5puAAAAwGc03QAAAIDPaLoBAAAAn9F0AwAAAD6j6QYAAAB8RtMNAAAA+IymGwAAAPAZTTcAAADgM5puAAAAwGc03QAAAIDPaLoBAAAAn9F0AwAAAD6j6QYAAAB8dlw13QPHDdRlYy472ptRbkNShmjguIFHezMklWxL27faHu3NQAVWmeddWmaaQoaGaOGmhb6va/TC0eo2upvv6ymL0QtHK2lY0tHejMMqZGiIxi0fd7Q345hXmee7H1LSUpT8avLR3gxJJdsSMjREmXszj/amHLeqHO0NGDhuoN5b9J4kKTw0XA0TG2pAmwF6vMvjqhJ61DdPkrQpa5Oe++Y5TVw5URt3b1TN2JpqW7ut7jvtPp3X5LzDtp7kV5N13+n36b7T7wt6jJS0FJ373rnmY2bcMEPdkrsd8tghQ0P0+dWf67KWlwW3cR4q036u7Cr6vNu6Z6uenPGkJq6cqM17NuuEqBPUpnYbPXnOkzqr4VlHe/OOuLTMNDV+rbH5mFF9Rmlg24GHPLaf8yE7P1vPzHxGny77VBt3bVR8ZLxa12it+0+/X31a9jns68PBVeT5HjI0xKw/1fUpDek25MhszFHg1/PvNrqb2tZuq1d7vhrchhnjzlw301nv2qirUgamHNZ1HkuO/tVVUs9mPTWqzyjlFuRq0spJunPSnQoPDddjXR474LF5hXmKCIs4YtuWlpmms949S0lRSfrrBX/VKbVOUX5hvqaunqo7J92p5XctP2LbUhZnNjhT6Q+kB/5975R7tSt3l0b1GRX4WdXoqoH/P9L706Wy7edjQUWed/0+7ae8wjy9d9l7anJCE23es1nT10xXRk7GEdsGv+QX5is8LPyQlmmQ0KDUvB7+7XBNWTVFXw34KvCzxMjEwP8XFhUqJCREoSFH983M2yfcru83fq83LnpDrWu0VkZ2hr7d8O0x8TpWlHNnWVXU+f7H4/qTnz/RkylPasVdKwI/i4uIC/x/cXGxCosLj/ovCgcT7D6rbM9/7NVjlVeYJ0nasHODOo/srK+u/0on1TxJkg7YB8Gc746EozV/K8THSyLDIlU7rrYaJTXS4E6DdX6T8/XFL19I+v2tque+eU51X66rFn9vIankxb7qP1cpaViSqr5YVX3G9FFaZlpgzMKiQt0/9X4lDUtStZeq6eFpD6tYxYe8bXdMvEMhCtG8m+epX+t+OrHaiTqp5km6/4z7NffmuYHHrd+5Xn3G9FHc83FKeCFBV/3nKm3O2hyor96+Wn3G9FGt4bUU93ycOr3TSV+t+f2C2W10N63buU5/nvpnhQwN8fzt1yUiLEK142oH/ouuEh3Yv7XjauutH95S53c6a+SCkWr8WmNFPRslqeRu16tzXy01Vtu32mpIypBAXZL6ftJXIUNDDni77INFHyj51WQlDkvUNf+9Rrtzdx/Sdle2/XwsqKjzLnNvpmatn6UXz39R5zY+V42SGqlzvc56rMtjurTFpYHHhQwN0cgFI9X3k76KeS5Gzd9ori9WfFFqrJ+3/KyL/n2R4p6PU63htXT959drW/a2QH3Kqik6+92zA9vb+6PeWr19tXPbCosKNWj8ILX8e0ut37lekjR++Xi1/2d7RT0bpSavNdHQlKEqKCootZ0j5o/QpR9fqtjnY/XcrOcOaX9IUlhoWKl5HRcRpyqhVQL/nrJqiuq8XEdfrPhCrf/RWpHPRmr9zvXqNrqb7ptyX6mxLhtzWeDjaV7zYeqqqWr1j1aKez5OPT/sqfTd6ToUX6z4Qo+f/bh6Ne+l5KRkdajbQXefdrcGtRsUeEzyq8l6ftbzGjR+kOJfiFfDVxrq7R/fLjWO13E3f+N8XfDBBar+UnUlDktU19FdtSB9gbltT814SnVerqPFmxdLkmavn60uo7oo+rloNXilge6ZfI/25O0ptZ3PzHxGAz4foIQXEnTrl7ce0r442irqfP/jcZ0YlagQhQT+vXzbcsW/EK/JKyerw9sdFPlspGavn63cglzdM/ke1fxrTUU9G6Wz3z1b8zfOD4x5sI9HjVs+rtTxvWjTIp373rmKfyFeCS8kqMPbHfTDbz8E6kfqeAjm+R/sIzz3Tbkv8PG0geMGaua6mXrt+9cC8/qPr9uPv/2ojm93VMxzMTrzX2dqxbYVKquq0VUD21cjtoYkqVpMtcDPqr1U7aDnuxHzR6jp600V8UyEWvy9hT5Y9EFgzIN9jC9zb6ZChoYoJS1FkrQjZ4f6j+2vGn+toejnotX8jeYa9dPvNxO9jlXXMX6kVYime3/R4dGB36Qkafra6VqRsULTrp+mCddOUH5hvnp82EPxEfGadeMszRk0R3ERJReFfcu9/N3LGr1wtN7t865m3zhb23O26/PUz0utZ/TC0WbTtT1nu6asmqI7O92p2IjYA+pJUUmSpKLiIvUZ00fbc7Zr5sCZmnb9NK3ZsUZX//fqwGOz8rLUq1kvTR8wXT/d9pN6Nu2pSz6+JHDhHnv1WNVPqK+nuz2t9AfSS/32e7it2r5Kn6V+prFXjdXC2xeWaZn5t5Sc0Eb1GaX0B9ID/5ak1TtWa9yKcZpw3QRNuHaCZq6bqWGzhwXqx+t+rmwqyryLi4hTXEScxi0fp9yCXHObh84cqqtaX6XFgxerV7Ne6j+2v7bnbJdUctLu/l53tavdTj/c+oOm9J+izVmbddV/rgosvydvj+4/4379cOsPmj5gukJDQtX3k74qKi46YF25Bbm68j9XauGmhZp14yw1TGyoWetmacC4Abr3tHu17M5l+mfvf2r0otF67pvSjfWQmUPUt2VfLRm8pFTDeThl52frxTkvauSlI7X0jqWqGVvTcxlrPmTnZ2v4d8P1Qd8P9M2N32j9zvV6cNqDgfq+z4f+8cK2v9pxtTVp1STPX8Jf/u5ldazbUT/d9pPu6HSHBk8cHGgEynLc7c7brRva3KDZg2Zr7k1z1bxqc/X6d6+Drre4uFh3T7pb7y9+X7NunKVTa52q1dtXq+eHPdWvVT8tvn2xPrniE81eP1t3Tb6r1LLDvxuuNrXa6KfbftIT5zzhuX8rsooy38vi0emPath5w5R6Z6pOrXWqHp72sD5L/UzvXfaeFty2QM2qNlOPD3sE5n5Z9B/bX/UT6mv+LfP1460/6tGzHlV4aMkd2Yp2POz//L281vM1nVH/DN3S/pbAvG6Q0CBQ/7+v/08vX/iyfrj1B1UJraJBX/x+TtrXAO9rdoOx//nu89TPde+Ue/XAGQ/o5zt+1m0dbtON42/UjLUzyjzmEzOe0LKtyzS5/2Sl3pmqERePUPWY6pLKdo6QDjzGj4YK9R5NcXGxpq+drqmrpuruzncHfh4bHquRl44MvBXw4eIPVVRcpJGXjlRISMlkHtVnlJKGJSklLUUXNr1Qr859VY+d/Zgub3W5JOmt3m9p6uqppdaXGJmoFtXcv+2s2r5KxSpWy+otze2evma6lmxeorX3rlWDxJID+/2+7+ukN0/S/I3z1aleJ7Wp3UZtarcJLPNM92f0+fLP9cWKL3RX57tUNbqqwkLCFB8Zr9pxtQ9hrx26vMI8vX/Z+4HfUsti32OTopIO2L6i4iKN7jNa8ZHxkqTrT71e09dO13MqaTyO1/1cWVS0eVcltIpG9xmtW768RW/9+Jba12mvro266pqTrznggjOwzUBde8q1kqTnz3ter897XfM2zlPPZj3193l/V7s67fT8ec8HHv9un3fV4JUG+iXjF51Y7UT1a92v1Hjv9nlXNf5aQ8u2LtPJNU8O/DwrL0sXf3SxcgtzNeOGGUqMKvkox9CZQ/XoWY/qhrY3SJKanNBEz5z7jB6e9rCe6vZUYPnrTr5ON7a70XoZyi2/KF9v9nqz1PHvxZoP+UX5euvit9S0alNJ0l2d79LTM58O1GPCY9SiWotAo3Iwb1/ytvqP7a9qL1VTm9ptdHaDs3VF6ysO+Fx+r+a9dEenOyRJj5z1iF6Z+4pmpM1Qi+ot9MnSTzyPu+6Nux+w3qRhSZq5bqZ6n9g78POCogL96fM/6af0nzT7xtmql1BPkvTC7BfU/5T+gc+1N6/WXK9f9Lq6ju6qERePUFSVkncEuzfurgfOfKDM+7ciqmjzvSye7va0Lmh6gaSSX5RH/DBCoy8brYuaXyRJeueSdzRtzTT9a8G/9NBZD5VpzPU71+uhMx8KXHeaV2seqFW04+GPz78sEqMSFREWoZjwmINe557r/py6JneVJD169qO6+KOLtbdgr6KqRCk8NFwtqrVQTHhM0Nu7//nu2s+u1cC2AwNz/P4z7tfcX+dq+HfDdW5j+zto+6zfuV7tardTx7odJUnJScmBWlnOEdKBx/jRUCGa7gm/TFDc83HKL8pXUXGRrjvlulJfHDil1imldtKiTYu0avsqxb8QX2qcvQV7tXr7au2st1PpWek6rf5pgVqV0CrqWLejiot/f+urb6u+6tuqr3O7/vhYS+q2VDVIbBBoBCWpdY3WSopKUuq2VHWq10lZeVkakjJEE1dOVPrudBUUFSinICdwB/ZIapTU6JAabi/JScmBhluS6sTV0ZY9WwL/Pl73c0VXUeedJPVr3U8Xn3ixZq2bpbm/ztXkVZP10pyXNPLSkaW+LPjHJjw2IlYJkQmBY2/R5kWasXaG4p6P2394rd6+WidWO1ErM1bqyZQn9f2v32tb9rbAHe71O9eXarqv/exa1U+or68HfK3o8Ojf98nmRZqzYU6pj4wUFhdqb8FeZednBy5c+y4UfooIiyjTXbCyigmPCTTc0oHzunO9zp7ftTin0Tlac88azf11rr7d8K2mr52u10a9pqHdhuqJrr/fGTy15u/bHRJS8vZ64HX0OO7UVNqctVl/+fovSlmXoi17tqiwqFDZ+dkHzPs/T/2zIsMiNffmuYG7ZFLJ67h482L9e8m/Az8rVrGKiou0dsdatarRSpLUsY7/r6NfKvJ89/LH+bN6x2rlF+XrrAa//+IWHhauzvU6K3VbapnHvP+M+3Xzlzfrg8Uf6Pwm5+vK1lcGjveKdjwc7vPHH88TdeLqSJK27NmihokNVS+hXrm/Q7X/9qZuTdWt7Ut//OasBmfpte9fK/OYgzsOVr9P+2lB+gJd2PRCXdbyMp3Z4ExJZTtHSAce40dDhWi6z218rkZcPEIRYRGqG1/3gC8JxIaX/shBVl6WOtTtoH9f/m/tr0bM4Wsmm1drrhCFaPm28n+J78H/Pahpa6Zp+AXD1axqM0WHR+uKT68o9dbHkbL//pSk0JDQA5rf/KL8Mo23/52ukJCQg74973Ks7ueKrqLOu32iqkTpgqYX6IKmF+iJrk/o5i9u1lMpT5Vquvf/gk6Ifj/2svKydEmLS/Ti+S8eMPa+C80lH1+iRkmN9M4l76hufF0VFRfp5BEnH3C89GrWSx8u+VDf/fpdqbuqWXlZGtptaOBO3/7bv8/BPjZ1uEVXiQ7c5dnncM/rYL4XEx4Wri6NuqhLoy565OxH9Ow3z+rpmU/rkbMfCVwAvV5Hr+PuhnE3KCMnQ6/1fE2NEhspskqkzvjXGQe8jhc0uUAf//yxpq6aqv6n9g/8PCsvS7d1uE33nHbPAetomNgw8P9H4nX0S0Wf75ZD3e+hIaEHHKv5haWP+yHdhui6U67TxF8mavKqyXoq5SmN6TdGfVv1rXDHw/7rKcvzs/xxvu07ZxzKNdtLMK+XVPoG3P7P56LmF2ndfes0aeUkTVszTee9f57u7HSnhl84vMzH6sF6nyOtQjTdseGxala1WZkf375Oe32y9BPVjK2phMiEgz6mTlwdff/r9zqn0TmSSt5W/PG3H9W+Tvsyr6dqdFX1aNZD/5j/D91z2j0HHEiZezOVFJWkVtVbacPODdqwc0PgLuyyrcuUuTdTrWu0liTN2TBHA9sMDPzGn5WXdcBnISPCIlRYVFjm7TucasTWUHrW75/n3JW7S2t3rC31mPDQcF+273jazxVJRZ13Lq1rtD6knOX2tdvrs9TPlJyUfNBv+2dkZ2hFxgq9c8k76tKoi6SSL08dzOBOg3VyzZN16ceXauJ1EwNvzbav014rtq04pP14JO0/rwuLCvXzlp91bvLvb+ke6fnQukZrFRQVaG/B3jLddSrLcTdnwxy92etN9WreS1LJl6r++IXZfS5tcakuOfESXTf2OoWFhumak68JrGPZ1mUV9nU8HCrbfHdpekJTRYRFaM6GOWqU1EhSSYM2f+P8wMdBasTU0O7c3dqTtydwPTlY1v6J1U7UiWecqD+f8Wdd+9m1GrVwlPq26lvhj4caMTX085afS/1s4eaFpX5RrkjXuVY1WmnOhjmBj+FJJXN233V7X2OcnpWudmon6eCvV43YGrqh7Q26oe0N6vJDFz007SENv3B4mY7ViqJCfpHSS/9T+6t6THX1GdNHs9bN0toda5WSlqJ7Jt+jX3f9Kkm697R7NWzOMI1bPk7Lty3XHRPvOCAQ/vPUz9Xy7/bniP/R6x8qLC5U55Gd9dmyz7QyY6VSt6bq9e9f1xn/OkOSdH6T83VKrVPUf2x/LUhfoHkb52nA5wPUtVHXwNsszas219jlY7Vw00It2rRI13123QG/WSYnJeub9d9o466NB71g+Kl7cnd9sPgDzVo3S0s2L9EN425QWGjYAds3fe10bcrapB05O8o8Nvv52HCk5l1Gdoa6v9ddHy7+UIs3L9baHWv1n6X/0UtzXlKfFmXPdr6z853anrNd1352reZvnK/V21dr6qqpunH8jSosKtQJ0SeoWnQ1vb3gba3avkpfr/1a90+93zne3afdrWe7P6veH/cONOdPnvOk3l/8voamDNXSLUuVujVVY34eo798/Zcyb6efuid318SVEzXxl4lavm25Bk8cfMDrEex8mLdxnlr+vaU27trofEy30d30zx/+qR9/+1FpmWmatHKSHp/+uM5tfG6ZL45lOe6aV22uDxZ/oNStqfr+1+/Vf2x/RVeJPuh4fVv11Qd9P9CN42/Uf5f9V1LJ58i/3fCt7pp0lxZuWqiVGSs1fvl43TXproOOcTw4ktfZQxEbEavBHQfroWkPacqqKVq2dZlu+fIWZedn66Z2N0mSTqt/mmLCY/T49Me1evtqfbTkI41eNDowRk5+ju6adJdS0lK0LnOd5qyfo/kb56tV9ZKPjVT046F74+764bcf9P6i97UyY6WemvHUAU14clKyvt/4vdIy00p9dM7Lxl0b1fLvLTVv47zDtr0PnfmQRi8crRHzR2hlxkr97bu/aWzqWD14ZskXs6PDo3V6/dM1bPYwpW5N1cy0mfrLjNLn0CdnPKnxy8dr1fZVWrplqSasnBD4mE9ZjtWKokLc6T5UMeEx+ubGb/TIV4/o8k8v1+7c3aqXUE/nNT4vcCJ/4MwHlJ6VrhvG3aDQkFANajtIfVv11c69OwPj7MzdqRUZdlROkxOaaMGtC/TcrOf0wP9KxqwRU0Md6nbQiItHSCp5e2b8NeN19+S7dc6ocxQaEqqezXrqjYveCIzztx5/06Dxg3Tmv85U9ZjqeuSsR7Qrd1epdT197tO6bcJtavp6U+UW5qr4qUN/KzdYj3V5TGsz16r3x72VGJmoZ8595oA73S9f+LLu/9/9emfBO6oXX09p96WVaWz287HhSM27uIg4nVbvNL0y9xWt3l7y+c0GCQ10S/tb9HiXx8u8vXXj62rOoDl65KtHdOGHFyq3IFeNkhqpZ9OeCg0JVUhIiMZcMUb3TL5HJ795slpUb6HXe76ubu91c4553+n3qai4SL3+3UtT/jRFPZr10IRrJ+jpb57Wi3NeVHhYuFpWb6mb291c5u3006B2g7Ro8yINGDdAVUKr6M+n/7nUXW4p+PmQnZ+tFRkrzI+r9GjaQ+8tek+Pf/24svOzVTe+rno3760nuz5Z5udQluPuX5f+S7dOuFXt326vBgkN9Px5z+vB/z3oHPOK1leoqLhI139+vUJDQnV5q8s1c+BM/d/X/6cuo7qouLhYTas21dUnXe0c41h3JK+zh2rY+cMCr9/u3N3qWLejpv5pqk6IPkFSybunH17+oR6a9pDeWfCOzmtynoZ0HaJbJ5R8rjgsNEwZORka8PkAbd6zWdVjquvylpdr6LlDJZV85rkiHw89mvXQE+c8oYenPay9BXs1qN0gDTh1gJZsWRJ4zINnPqgbxt2g1v9orZyCHK29d60x4u/yi/K1ImOFsvOzD9v2XtbyMr3W8zUN/2647p1yrxqf0Fij+owq9Uf63r30Xd30xU3q8HYHtajeQi+d/5Iu/PDCQD0iLEKPTX9MaZlpig6PVpeGXTSm3xhJZTtWK4qQ4rJ+iw0VxpCUIUrLTNPoy0Yf7U0BcJiMXjhaoxeO5q+5AceQlLQUDRw3sMw3qXBsq5QfLwEAAAAqE5puAAAAwGeV8jPdx7tuyd0O+LIKgMqtbe22peIQAVR+yUnJgVQVgM90AwAAAD7j4yUAAACAz2i6AQAAAJ+V+TPd+/954SPBWqfXp2LKs6wfkpOTnbUBAwaYyxYVuUPtY2JinLXIyEhz3KFDhzpru3btctYq2r6tiCrLfjga8xqorJjXx44hQ4Y4a5mZmc5adradX21dry3h4eFmPSwszFlr3Lixs/bAAw8EtT3HkyM5r7nTDQAAAPiMphsAAADwGU03AAAA4DOabgAAAMBnNN0AAACAz2i6AQAAAJ+V+S9SVrbIwGDH9XqewcYBLV261Flr1qyZuWxERISzlpeX56x57aOXXnrJWXvyySfNZYN1vMQNVpbnQrQYUHbM62PH0XgtrXV6vWYFBQXOWpUq7vTnnj17OmtTp04113m8IDIQAAAAOIbQdAMAAAA+o+kGAAAAfEbTDQAAAPiMphsAAADwGU03AAAA4DOabgAAAMBn7nDHCqA8mc5hYWHOmpW1HWwOtyTdc889zlpcXJyztmrVKnNcK4t7x44dzlp8fLw57jXXXOOsffvtt87alClTzHGDVZ5s2cqSnwsAODK6devmrFnXjF9++cWHrSnf3wjJzs521urWreusde7c2Vkjp/vI4043AAAA4DOabgAAAMBnNN0AAACAz2i6AQAAAJ/RdAMAAAA+o+kGAAAAfBZSXMastfLEuQWrPPE6VvSftexDDz1kjnvzzTc7a1WquBMYc3NznbWIiAhznVYsoLXsnj17zHGtZWNiYpw1K7roxRdfNNf56aefmnUXr9e7okUGVrTtcTka8xqorJjXlcsjjzzirL3wwgvO2sqVK50169roxepLCgoKzGWt/iI6OtpZW7JkibN23nnnmes8XhzJec2dbgAAAMBnNN0AAACAz2i6AQAAAJ/RdAMAAAA+o+kGAAAAfEbTDQAAAPjMnUFTAVgxLl4RL7Vr13bWfvzxR2ctIyPDHNeK79u1a5ezZkU4JSUlmeusVauWs5aWluaseUUG5ufnO2vW/j3hhBOctf/7v/8z1/nss886a61atXLWCgsLzXEBAPij2NhYZ826xlnxfVb8r9e45VnOugbm5OQ4a9Y+wJHHnW4AAADAZzTdAAAAgM9ougEAAACf0XQDAAAAPqPpBgAAAHxG0w0AAAD4rEJHBloxe17xOt98842ztmXLFmfNKzIwLCwsqJoV92NFDUrShg0bzLpLdHS0WY+KinLWIiMjg1qn1/6rUaOGs/bpp586a/369TPHLc+xAgA49ljXsaKiImctNNR9P9KqSfZ11apZccSSHWNo4fpXsXCnGwAAAPAZTTcAAADgM5puAAAAwGc03QAAAIDPaLoBAAAAn9F0AwAAAD6j6QYAAAB8VqFzuq18ySeffDLoZbdu3eqsWTmakpSfn++sWbmf1vZYGd5e4yYmJjprVna113qzs7OdtSpV3IeNta2SnePdrFkzZ61NmzbmuIsWLTLrAADsY/1dDes6Hx4ebo5r/d2N3377zVlr3ry5Oa61rHVN3rt3rzkujizudAMAAAA+o+kGAAAAfEbTDQAAAPiMphsAAADwGU03AAAA4DOabgAAAMBnFToy0HLzzTebdSuaLjc311nziu+zonm8lg1mTEmKiIhw1qxYQCumsDzblJeX56xlZWWZ49arV89ZCw11/w542223mePecccdZh0AcHxZvnx5UMtZ1/KkpCRz2VmzZjlr//d//+esLV261Bx3zZo1zlqtWrWctW3btpnj4sjiTjcAAADgM5puAAAAwGc03QAAAIDPaLoBAAAAn9F0AwAAAD6j6QYAAAB8VqEjA+Pi4py1yMhIc9mYmBhnrVq1as5adna2OW5+fr6zFh4eHtRyXgoKCpy18sQCWrFIRUVFzpoV7RcdHW2uMyoqynvDDqJRo0ZBLYeKx4q5tI4tKfhYzrCwsKDH9Vo2WNZ+sOZ8zZo1zXEvueQSZ61nz57O2qpVq5y1xx57zFyntY+Cfc2A8lq8eLGzZs2/YGuSHbfr1V9YrGuy1StZ+wBHHne6AQAAAJ/RdAMAAAA+o+kGAAAAfEbTDQAAAPiMphsAAADwGU03AAAA4DOabgAAAMBnFTqnu379+s6aV1amlQ1bntxYK4/Wysz22l6LlftZnpxu67kEmw3ulWmcmJjorOXm5jprERER5rioPKwsbiuL1k/Bzs+jkUG9e/dusz5y5EhnzcoJ7t27d9DbdDT2g3VOyMvLc9a8cs5POumkoLcJFcvy5cuDWs76OyBe1zhrjpXnem0ta82Fn3/+Oeh14vDjTjcAAADgM5puAAAAwGc03QAAAIDPaLoBAAAAn9F0AwAAAD6j6QYAAAB8VqEjAxs3buysecVm5eTkOGtWZNTGjRvNcatWreqs7dy501mLiopy1qx4K8mOL7LGLU+MlxWhZkUXWXFwkv1crO21nicqF78iO/2KrQt23Pbt25v1F154wVm7/vrrnTUrSlWSPvroI2ctLS3NWbv//vudtSuuuMJc55133mnWg2W93nPnznXWXn31VWft22+/NddJZOCxY8+ePc5afn6+s2Zd/6xrmCTt2rXLWYuOjjaXtVjrtWKFlyxZEvQ6cfhxpxsAAADwGU03AAAA4DOabgAAAMBnNN0AAACAz2i6AQAAAJ/RdAMAAAA+q9CRgbVr13bWsrOzzWXj4uKCqnnFg1kRRBEREc6aFaVXUFBgrjM8PNyXca2YISsW0BrXimGS7CjHoqIiZ82KecTxI9j4vvLECVpRXc8884yz1rFjR3Nca17ffffdztpnn31mjjty5Ehn7emnn3bW/vvf/zprN9xwg7nO+fPnO2u9e/d21qxIQEkaMWKEs5aamuqsTZgwwVm74447zHVmZmaadRwbNm/e7KxZ10Zr3krS1q1bgxrXi7Ws1ZesWrUq6HXi8ONONwAAAOAzmm4AAADAZzTdAAAAgM9ougEAAACf0XQDAAAAPqPpBgAAAHxWoSMDragurzi8pKQkZ82KDLQi+CQpLy/PrLtYcYLW85SkkJAQZ82KLwp2WyU7ymvv3r3OmtdzsaLbrLjBqKgoc1ygQYMGzlpsbKy57JVXXumsWZF35ZljV1xxhbN2zz33OGtXX321Oe7LL7/srM2YMcNZGzhwoLNmRRhK0tSpU521WbNmOWu5ubnmuK1bt3bW2rRp46w1btzYWWvYsKG5zoyMDLOOY0N6erqzZsUVW9djSdq9e7ezlpCQ4L1hDta13oopRMXCnW4AAADAZzTdAAAAgM9ougEAAACf0XQDAAAAPqPpBgAAAHxG0w0AAAD4jKYbAAAA8FmFzum2cimtHGlJiomJcdasbF0rT1uSEhMTnTUrZ9rKFY+OjjbXuWfPHmfNyr2uVq2aOa6VkWtljVr73uu5VKniPuSs/G/reUp2vnpRUZG5LCoPa/5de+21zlq/fv3Mca3j1ponc+bMcda+/PJLc52dO3d21r744gtn7bTTTjPH7dmzp7P25JNPOmtr1qxx1qxMcUk66aSTnLWbbrrJWbvrrrvMcQcPHuysWXna5513nrM2efJkc50nnniiWcexwTre69SpE/S41vXR6+8FBDtuWlpa0OPiyOJONwAAAOAzmm4AAADAZzTdAAAAgM9ougEAAACf0XQDAAAAPqPpBgAAAHxWoSMDrWg/K05QsiPA0tPTnTUrek6yo/8SEhKcte3btztr1vOU7PhDK86suLjYHDcuLi6oZXft2uWsecXz7dy501krT+xfUlKSs2bte7hFRkaadSv+KthoLK8o0IYNGzpr1lxYunSpOW5OTo6zNmLECGetSZMmzlpWVpa5TuuYbdasmbP2ww8/mOPefPPNzlpycrKzNm/ePGetZcuW5jofeOABZ2369OnOWtWqVc1x69Wr56x16tTJWbPOUV7XDq86jg1bt2511qxrUUhIiDnu+vXrnbWoqCjvDQtivatWrQp6XBxZ3OkGAAAAfEbTDQAAAPiMphsAAADwGU03AAAA4DOabgAAAMBnNN0AAACAzyp0ZKAVueUVvVOlivupZWdnO2tekYFWLFliYqKzZsX9eEUQeW2Ty549e8y6FUVYo0YNZ23btm3OWq1atbw3zGHHjh3OmleMV+3atZ01IgPdTjvtNGfNK77PmgvWMW1FVZZnndZxeeutt5rjWlF6Vnzf3r17g1pOkvLz85016xxl7QNJ+vzzz521nj17Omtnn322s/bzzz+b62zQoIGzZh1j119/vTnuTz/95KxZ54SVK1c6a4WFheY6vc7HODZYMaJXXnmls2adZyT7OuY1dy3Wcblhw4agx8WRxZ1uAAAAwGc03QAAAIDPaLoBAAAAn9F0AwAAAD6j6QYAAAB8RtMNAAAA+IymGwAAAPBZhc7pLioqCnpZKw+zoKDAWfPK/7Yys61xre2Jjo421xkRERHUuHl5eea4Vk5wcXGxs2bl3Hqts2bNms6atW+9jgUrVxxuderUCXrZ9PR0Z806Lq38/cjISHOd1rH322+/OWt9+/Y1xw02m3njxo3OmpWDL0mxsbHO2po1a5y1jIwMc9ycnBxnbcKECc5ajx49nLXu3bub67ReF+t5eu1363jYuXOnuayL1+tiHZ84dljHj/X3Arz+boaV023Nay/WevlbFJUHd7oBAAAAn9F0AwAAAD6j6QYAAAB8RtMNAAAA+IymGwAAAPAZTTcAAADgswodGWjFRXlFyFmxWbVq1XLWNm/ebI5rxV9ZEhISnDWv2Cwrfs3iFaNnxSNa+75atWrO2p49e8x1WjGFVjSi1+ttvaZws45n63WWpL179zprVoScNTfDw8PNdVrHjxVXuW3bNnPcuLg4Z82KkLO2Nzs721yntU3W8XzyySeb41oRpNac3717t7PmFc9nRU9WqeK+zPz000/muNb+rV+/flA1r3PUrFmzzDqODaeddpqzZkXmVq1a1Rx369atzppX3KfFijFs37590OPiyOJONwAAAOAzmm4AAADAZzTdAAAAgM9ougEAAACf0XQDAAAAPqPpBgAAAHxWoSMDrZg9rxg9a1krziw1NdUct0OHDs6aFRFWUFBgjmtJSkpy1qwINSuaTbJj+Kz4MCtebd68eeY6GzRo4KxZMU1WHJxkR6HBbdKkSc7aBRdcYC574oknOmtWbNamTZucNa95bdWtOeYVKbl9+3ZnzYpOjI+Pd9a8okCbN2/urFnzzzp/SdLixYudNWv/tW7dOuh1WtF/VjRiTEyMOa4Ve2rt3wULFjhrXrFtW7ZsMes4NtStW9dZ85q7lhUrVgS9rMXaJq5/lQd3ugEAAACf0XQDAAAAPqPpBgAAAHxG0w0AAAD4jKYbAAAA8BlNNwAAAOCzCh0ZaEV1ebHi8ObMmeOseUWWWXF54eHhzlpYWJiz5hVPZG2Ttc7o6Ghz3CpV3C9/aKj79zGrtnz5cnOdl112mbO2a9euoNYpSbGxsWYdB7djxw5nbfz48eayderUcdbOP/98Z61z587OWlZWlrnOzMxMZ806frxERkY6a9axt2fPHmfNK2Zv9uzZztrq1audtc2bN5vjWueoNm3aOGtW3KdX/Kh1frPiPq3XU7KPT6/9C1iaNm3qrJUn4tcv1hyzzl+oWLjTDQAAAPiMphsAAADwGU03AAAA4DOabgAAAMBnNN0AAACAz2i6AQAAAJ/RdAMAAAA+q9A53VbOtFdGq1X/4YcfnLXhw4eb45500knOWlpamrmsi1fG5vbt24Matzys/O/8/Pygx33iiSecteLi4qDXWbt27aC3CQfnlVlvHe8jR4501qxM9ebNm5vrtLJ1rdz51NRUc1zr2LPs3r3bWfPKDbcyya1M3qioKHNcKxd7zZo1zpo1xzIyMsx1euWrB8v6GwZWzdp/Vk0i//t4YR3T9evXD3pcq2/xyru3WH8voDzXZBxZ3OkGAAAAfEbTDQAAAPiMphsAAADwGU03AAAA4DOabgAAAMBnNN0AAACAzyp0ZKAVrxMREWEua8Vqffnll0Fv09KlS4Ne1mXPnj2Hfczy8iuCaOXKlc5ajRo1nDWv+LqioqKgtwlHlnW8L1y40FzWq36ssGLrvM4XVn3Hjh1Bb9PREGyUY0FBQVA1HD+sa5xXrKTF6k3KExloRWQSGVh5cKcbAAAA8BlNNwAAAOAzmm4AAADAZzTdAAAAgM9ougEAAACf0XQDAAAAPqvQkYHBxkVJduTPihUrgh63ShX3LrNi60JD3b/feD3P8uwHixVBZK2zPPF8qampzpoVGei1D4gMBACUlRUrbMnMzDTrVo9QHlZPU54oQhxZ3OkGAAAAfEbTDQAAAPiMphsAAADwGU03AAAA4DOabgAAAMBnNN0AAACAz2i6AQAAAJ9V6JzuwsLCoJdNS0s7fBvyB9Y2+ZVtHSwrh1sKfpuCzfeWpB9//NFZO+ecc5y1vLw8c9yCggKzDgDAPsH+XQ2v62p+fn7Q22Qpz3UXFQd3ugEAAACf0XQDAAAAPqPpBgAAAHxG0w0AAAD4jKYbAAAA8BlNNwAAAOCzCh0ZmJWV5ax5RcRZ8Trlid6xooSCjTj0iiCqaHFA5dkHixYtOuzrlKRdu3YFNS4A4PhjxdB6XW8swUbxbtu2zaxHRUU5axWtR4Abd7oBAAAAn9F0AwAAAD6j6QYAAAB8RtMNAAAA+IymGwAAAPAZTTcAAADgswodGXjqqac6a+Hh4eayMTExzlp5Iu/8iAz0K+7Hr3HLsw+2bNnirEVGRjprVlySJHXs2NGsAwCwz7p165y1Ll26OGt79+41x7Wiji1WhKFkXwM3b94c1Dpx5HGnGwAAAPAZTTcAAADgM5puAAAAwGc03QAAAIDPaLoBAAAAn9F0AwAAAD6r0JGB8+bNc9YiIiLMZa3IwGCj/SSpqKgo6GUrk5CQEGetPPtg48aNztrChQudNa9IpJ07dwa7SQCA48z333/vrA0aNMhZi4uL82NzzGuuZEf1Llmy5HBvDnzCnW4AAADAZzTdAAAAgM9ougEAAACf0XQDAAAAPqPpBgAAAHxG0w0AAAD4jKYbAAAA8FlIcXFxcZke6JEheazwep5l3F2VnrUfjpd9UB6VZR8dL/MaOByY18eOs88+21mbPHmys7Z9+3Zz3EaNGgW1PRs2bDDr1np79+4d9Lg4svOaO90AAACAz2i6AQAAAJ/RdAMAAAA+o+kGAAAAfEbTDQAAAPiMphsAAADwWZkjAwEAAAAEhzvdAAAAgM9ougEAAACf0XQDAAAAPqPpBgAAAHxG0w0AAAD4jKYbAAAA8BlNNwAAAOAzmm4AAADAZzTdAAAAgM/+Hwcl/CxOGhJ0AAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# Plot predictions\n",
"plt.figure(figsize=(9, 9))\n",
"nrows = 3\n",
"ncols = 3\n",
"for i, sample in enumerate(test_samples):\n",
" # Create a subplot\n",
" plt.subplot(nrows, ncols, i+1)\n",
"\n",
" # Plot the target image\n",
" plt.imshow(sample.squeeze(), cmap=\"gray\")\n",
"\n",
" # Find the prediction label (in text form, e.g. \"Sandal\")\n",
" pred_label = class_names[pred_classes[i]]\n",
"\n",
" # Get the truth label (in text form, e.g. \"T-shirt\")\n",
" truth_label = class_names[test_labels[i]] \n",
"\n",
" # Create the title text of the plot\n",
" title_text = f\"Pred: {pred_label} | Truth: {truth_label}\"\n",
" \n",
" # Check for equality and change title colour accordingly\n",
" if pred_label == truth_label:\n",
" plt.title(title_text, fontsize=10, c=\"g\") # green text if correct\n",
" else:\n",
" plt.title(title_text, fontsize=10, c=\"r\") # red text if wrong\n",
" plt.axis(False);"
]
},
{
"cell_type": "markdown",
"id": "5ce6dc44-90a5-48c3-91a5-810fa084d98b",
"metadata": {
"id": "5ce6dc44-90a5-48c3-91a5-810fa084d98b"
},
"source": [
"Well, well, well, doesn't that look good!\n",
"\n",
"Not bad for a couple dozen lines of PyTorch code!"
]
},
{
"cell_type": "markdown",
"id": "ab108078-6770-4cb9-ac62-a761ff159aba",
"metadata": {
"id": "ab108078-6770-4cb9-ac62-a761ff159aba"
},
"source": [
"## 10. Making a confusion matrix for further prediction evaluation\n",
"\n",
"There are many [different evaluation metrics](https://www.learnpytorch.io/02_pytorch_classification/#9-more-classification-evaluation-metrics) we can use for classification problems. \n",
"\n",
"One of the most visual is a [confusion matrix](https://www.dataschool.io/simple-guide-to-confusion-matrix-terminology/).\n",
"\n",
"A confusion matrix shows you where your classification model got confused between predicitons and true labels.\n",
"\n",
"To make a confusion matrix, we'll go through three steps:\n",
"1. Make predictions with our trained model, `model_2` (a confusion matrix compares predictions to true labels).\n",
"2. Make a confusion matrix using [`torchmetrics.ConfusionMatrix`](https://torchmetrics.readthedocs.io/en/latest/references/modules.html?highlight=confusion#confusionmatrix).\n",
"3. Plot the confusion matrix using [`mlxtend.plotting.plot_confusion_matrix()`](http://rasbt.github.io/mlxtend/user_guide/plotting/plot_confusion_matrix/).\n",
"\n",
"Let's start by making predictions with our trained model."
]
},
{
"cell_type": "code",
"execution_count": 53,
"id": "065b8090-c9c5-43df-b5c1-b45ba33af1be",
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/",
"height": 49,
"referenced_widgets": [
"d3ab200da5f940d5b45396f83bd835e2",
"f35a13b3e55342aeb24b188c1d81a9e5",
"4a282c1974524bd3a7eba45fd3112129",
"44d4196e99a4412f893ba8ac4672915d",
"12d1a54d4107428eae2e64ff0a255c50",
"4d6eb654b2794b0a95f31ac94b52a4ca",
"fe5cff037f714657996f0541baee39f3",
"0670e3e758e6486b9cf4e2797b4b619a",
"3c590fc27b624584ba564e18bc42a2e4",
"629ca5b704b84a958d4ee477907f64a1",
"4d7c25dcdde8414382be4cf63a9cacf9"
]
},
"id": "065b8090-c9c5-43df-b5c1-b45ba33af1be",
"outputId": "92a8bee2-71f5-4504-d534-cc63138c413d"
},
"outputs": [
{
"data": {
"application/vnd.jupyter.widget-view+json": {
"model_id": "d3ab200da5f940d5b45396f83bd835e2",
"version_major": 2,
"version_minor": 0
},
"text/plain": [
"Making predictions: 0%| | 0/313 [00:00 prediction probabilities -> predictions labels\n",
" y_pred = torch.softmax(y_logit, dim=1).argmax(dim=1) # note: perform softmax on the \"logits\" dimension, not \"batch\" dimension (in this case we have a batch size of 32, so can perform on dim=1)\n",
" # Put predictions on CPU for evaluation\n",
" y_preds.append(y_pred.cpu())\n",
"# Concatenate list of predictions into a tensor\n",
"y_pred_tensor = torch.cat(y_preds)"
]
},
{
"cell_type": "markdown",
"id": "362002d9-ec41-4c74-a210-b5d4f53410c4",
"metadata": {
"id": "362002d9-ec41-4c74-a210-b5d4f53410c4"
},
"source": [
"Wonderful!\n",
"\n",
"Now we've got predictions, let's go through steps 2 & 3:\n",
"2. Make a confusion matrix using [`torchmetrics.ConfusionMatrix`](https://torchmetrics.readthedocs.io/en/latest/references/modules.html?highlight=confusion#confusionmatrix).\n",
"3. Plot the confusion matrix using [`mlxtend.plotting.plot_confusion_matrix()`](http://rasbt.github.io/mlxtend/user_guide/plotting/plot_confusion_matrix/).\n",
"\n",
"First we'll need to make sure we've got `torchmetrics` and `mlxtend` installed (these two libraries will help us make and visual a confusion matrix).\n",
"\n",
"> **Note:** If you're using Google Colab, the default version of `mlxtend` installed is 0.14.0 (as of March 2022), however, for the parameters of the `plot_confusion_matrix()` function we'd like use, we need 0.19.0 or higher. "
]
},
{
"cell_type": "code",
"execution_count": 54,
"id": "e6c0a05d-d3e0-4b86-9ef7-ee6ea5629b07",
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/"
},
"id": "e6c0a05d-d3e0-4b86-9ef7-ee6ea5629b07",
"outputId": "b37df16c-c292-4347-807c-91c97bf81f20"
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"\u001b[2K \u001b[90m━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━\u001b[0m \u001b[32m519.2/519.2 kB\u001b[0m \u001b[31m10.8 MB/s\u001b[0m eta \u001b[36m0:00:00\u001b[0m\n",
"\u001b[2K \u001b[90m━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━\u001b[0m \u001b[32m1.4/1.4 MB\u001b[0m \u001b[31m54.9 MB/s\u001b[0m eta \u001b[36m0:00:00\u001b[0m\n",
"\u001b[?25hmlxtend version: 0.22.0\n"
]
}
],
"source": [
"# See if torchmetrics exists, if not, install it\n",
"try:\n",
" import torchmetrics, mlxtend\n",
" print(f\"mlxtend version: {mlxtend.__version__}\")\n",
" assert int(mlxtend.__version__.split(\".\")[1]) >= 19, \"mlxtend verison should be 0.19.0 or higher\"\n",
"except:\n",
" !pip install -q torchmetrics -U mlxtend # <- Note: If you're using Google Colab, this may require restarting the runtime\n",
" import torchmetrics, mlxtend\n",
" print(f\"mlxtend version: {mlxtend.__version__}\")"
]
},
{
"cell_type": "markdown",
"id": "5245ede6-fd7f-40ad-a0b3-ae678544b84a",
"metadata": {
"id": "5245ede6-fd7f-40ad-a0b3-ae678544b84a"
},
"source": [
"To plot the confusion matrix, we need to make sure we've got and [`mlxtend`](http://rasbt.github.io/mlxtend/) version of 0.19.0 or higher."
]
},
{
"cell_type": "code",
"execution_count": 55,
"id": "21383f88-a2dd-4678-94c6-479c592da0ab",
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/"
},
"id": "21383f88-a2dd-4678-94c6-479c592da0ab",
"outputId": "faffbe4c-9c86-4a20-cbd6-c7e8e48e81a5"
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"0.22.0\n"
]
}
],
"source": [
"# Import mlxtend upgraded version\n",
"import mlxtend \n",
"print(mlxtend.__version__)\n",
"assert int(mlxtend.__version__.split(\".\")[1]) >= 19 # should be version 0.19.0 or higher"
]
},
{
"cell_type": "markdown",
"id": "c91b9346-e25f-48ab-967e-425649331dc6",
"metadata": {
"id": "c91b9346-e25f-48ab-967e-425649331dc6"
},
"source": [
"`torchmetrics` and `mlxtend` installed, let's make a confusion matrix!\n",
"\n",
"First we'll create a `torchmetrics.ConfusionMatrix` instance telling it how many classes we're dealing with by setting `num_classes=len(class_names)`.\n",
"\n",
"Then we'll create a confusion matrix (in tensor format) by passing our instance our model's predictions (`preds=y_pred_tensor`) and targets (`target=test_data.targets`).\n",
"\n",
"Finally we can plot our confision matrix using the `plot_confusion_matrix()` function from `mlxtend.plotting`."
]
},
{
"cell_type": "code",
"execution_count": 56,
"id": "7aed6d76-ad1c-429e-b8e0-c80572e3ebf4",
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/",
"height": 667
},
"id": "7aed6d76-ad1c-429e-b8e0-c80572e3ebf4",
"outputId": "ae34ae74-2038-4037-f01d-77a807e4de9b"
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAApYAAAKKCAYAAACH5hvqAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/bCgiHAAAACXBIWXMAAA9hAAAPYQGoP6dpAADaa0lEQVR4nOzdd1QU198G8GfpvUkT6aAoKhZU7AUb9t5iQyJGY0OsaGzYY8NujAVNYiyxIXYRCzbsPRbUYJSmSFdAlvcPftlkFZUyMLu8z+ecOcedvTP7XC47fHd25irJzc3NBRERERFRMamIHYCIiIiIygYWlkREREQkCBaWRERERCQIFpZEREREJAgWlkREREQkCBaWRERERCQIFpZEREREJAg1sQNQ8UmlUrx69Qr6+vqQSCRixyEiIqIyJjc3F6mpqbCysoKKyufPS7KwLANevXoFGxsbsWMQERFRGffixQtYW1t/9nkWlmWAvr4+AECz3WJI1LVFTiOsv7YMFDtCiZBKy+Z/ePWhjPZLXbXsfRNQVr/dSEzNFDtCiTDR1xQ7Qokoq8dCFZWy9/5KTUmBs4ONrOb4HBaWZcA/fyAk6tplrrA0MDAQO0KJKKsHUxaWyqOsFpbZkrJZWBqwsFQqZbGw/MfXjh28eYeIiIiIBMHCkoiIiIgEwcKSiIiIiATBwpKIiIiIBMHCkoiIiIgEwcKSiIiIiATBwpKIiIiIBMHCkoiIiIgEwcKSiIiIiATBwpKIiIiIBMHCkoiIiIgEwcKSiIiIiATBwpKIiIiIBMHCkoiIiIgEwcKSiIiIiATBwpKIiIiIBMHCkoiIiIgEwcKSiIiIiATBwpKIiIiIBFEmC8tZs2ahZs2aX2zTvHlz+Pn5lUoeRaeiIsGMvrVxf00vvPltEO6u7okpPWvItflpZBNk/OEjtxyY1kb2vK2ZHtaNaCy3jx9614K6muL/iq1fuwYuzvYw0tNCk4YeuBIZKXakYktNTcXE8X6oXNEe5Qx14NmsEa5dvSJ2rELZuGEdGtatCWtzI1ibG6FVs0Y4ceyI7Pn3799jvN8o2Fcwg5WpAQb07Yn4uDgRExfN3MBZ0NFQkVtqVqsidqxiW7xoARrVrwszY33YWpmjV4+uePTwodixCi0tNRUzAybAw60inKyM0KVtc9y8fjXftlP8R8HaRAsb160q5ZTCKUvHw5ycHATOmg7XSo4oZ6iDapWdsXD+HOTm5oodTRCKOlYK8VdfIpF8cZk1a5bgr7l3717MmTPni22eP38OiUSCmzdv5vv87NmzMWDAAAB5fdi/f7/AKUvH+K7VMbRNZfhvuohafnvxw69XMa6LG0a0d5Vrd/zG33AY+rtsGRx0WvacSwVDqEiA0RvOw33cPkwOvoxv21TG7G/cS7k3hbN7105MnuiPaT/MxMXI63Bzq4HOHdoiPj5e7GjFMnK4L8LDTmLj5m2IvHYbLVu1Rsd2rfHq5UuxoxVYhQrWmDVnPs5cuILT5yPRtHkL9OvVDQ/u3wMABEzyx9FDodj6204cOh6O2JgYDOjbU+TURePqWhVPo1/JlpOnz4kdqdjOnT2D4SNG4kzEJYQeOYEP2dno2L4N0tPTxY5WKBPHjsC502FYsX4zTkZcQ9MWLdGvW3vEvJJ/Lx0JPYDrVyNhUd5KpKTFV9aOh8uWLMLGDeuxLGgVrt+6jznzF2L50sVYt0Z5C/9/KPJYKURhGRMTI1uCgoJgYGAgt27ChAmCv6aJiQn09fU/+3xWVtZX93HgwAF07txZyFiiqO9ijkNXonH0+t+ITkjD/kvPEXbrJeo4m8q1y8zOQVzSO9mSlP7vz+jEzZf4bm0Ewm69wvP4VBy6+gIrQu6gi4d9KfemcFYGLcOQb30xyHsIqri6YtXa9dDW0cHW4M1iRyuyd+/eYf++PZg7fxEaN2kKJ2dnTJs+C45Ozvh5wzqx4xVYuw6d0MarPZycK8K5YiXMmD0Xunp6uBJ5CcnJyfgleDPmLVqCZs09Uau2O9Zu2ITLly7gyuVLYkcvNFU1NVhaWsoWU1PTr2+k4EIOHcXAwd5wrVoVbjVqYMOmYLyIjsaN69fEjlZg7969w+GD+zBt9nzUb9gEDo5OGD9lOuwdnfDLlg2ydjGvXmL6ZH+s+ikY6mpqIiYunrJ2PLx08SI6dOoMr/YdYGdvj27de6Jlqza4qmTf3uRHkcdKIQrL/x5QDQ0NIZFI5Nbp6el9ss3p06dRr1496OrqwsjICI0aNcJff/0l1+aXX36Bvb09DA0N0bdvX6Smpsqe+/ircHt7e8yZMweDBg2CgYEBhg0bBgcHBwBArVq1IJFI0Lx5c1n7Fy9e4N69e/Dy8oK9vT0AoFu3bpBIJLLHALBu3To4OTlBQ0MDLi4u+OWXX+QySiQSrFu3Du3atYO2tjYcHR3xxx9/FPEnWTSXHsajefXycC5vAACobmeCBpUtcPzG33LtmlS1xPNN/XBzRQ+s8G0AEz3NL+7XUEcDb9MySyx3cWVlZeHG9WvwbNlKtk5FRQWenq0QeemiiMmK58OHD8jJyYGmlpbcem1tbVy8cF6kVMWTk5ODP3btQEZ6Oup5NMDNG9eQnZ2N5p7/jl0ll8qwsbFFpBIWllFPHsPRrgJcXZwwZNAAvIiOFjuS4FKSkwEAxsYmIicpuJx/3kua8sc6LS0tRF66AACQSqUYO8IHw0ePg0sV1/x2oxTK4vGwfoMGOB1+Co8fPQIA3L59CxcuRKBNWy+RkxWPoo+VQhSWhfXhwwd07doVzZo1w+3bt3Hx4kUMGzYMEolE1iYqKgr79+9HaGgoQkNDcebMGSxcuPCL+12yZAlq1KiBGzduYPr06Yj83/UKJ0+eRExMDPbu3StrGxISgubNm8PAwABXruR9+tmyZQtiYmJkj/ft24exY8di/PjxuHv3Lr777jsMGTIE4eHhcq87ffp09OjRA7du3UL//v3Rt29fPHjw4LM5MzMzkZKSIrcUx5J9t7H7/DPcXNEDyTu8cXFxF6w5dA87zz2VtTlx82/4rjqLDrOPYvqvV9DY1RL7p7WBiook3306WupjeDtXbDrxZ7GylaTXr18jJycH5uYWcuvNLSwQGxsrUqri09fXh0f9Bli0YC5iXr1CTk4Oft/+Ky5fuojYmBix4xXKvbt3YGVqADNDbfiP+R6/7dyDylVcER8bCw0NDRgZGcm1NzO3QFycco1d3Xoe2LBxCw4cPIIVq9bi+fNnaOXZVO6DsLKTSqWYON4PDRo2QtVq1cSOU2B6+vpwr1sfQUsWIDYm7720Z9d2XLtyGfH/+z1bu2IJ1FTV8O13I0VOWzxl8Xg4fuIU9OzVB7XcqsBQVwMN69XGyNFj0bdff7GjFYuij5VSnrNPSUlBcnIyOnbsCCcnJwBAlSryF7tLpVIEBwfLvu4eOHAgwsLCMG/evM/u19PTE+PHj5c9VlVVBQCUK1cOlpaWcm0PHDiALl26AADMzMwAAEZGRnLtlixZAm9vb3z//fcAAH9/f1y6dAlLlixBixYtZO169eqFoUOHAgDmzJmDEydOYNWqVVi7dm2+ORcsWIDZs2d/th+F1aOhA/o2cYT3itN48CIJbvYm+HGIB2ISM/DbmScAgD/OP5O1vxf9Fnf+eov7a3uhaVVLnL4jX6xYmejgwLS22HfxGbacfCRYTiq4jZu3YcR338LZwRqqqqqoWas2evXph5tK9DUkAFSs5IJzl68jJTkZB/btwXDfITh8PPzrGyqRtl7tZP+u7uaGuvU8UNnZHnv+2AXvId+KmEw4fqNH4t69uwg7HSF2lEJbsX4Txo/+DnWqOkJVVRXVatRClx69cefmDdy+eR2bflqDI+EX5U5skGLY88cu7NyxHVu2/YYqrlVx+9ZNTJ4wDuXLW2HAwMFixyuzFP6MZXR0NPT09GTL/PnzYWJiAm9vb7Rt2xadOnXCihUrEPPRmRh7e3u5ayjLly//1Yta69SpU6BMKSkpOHPmzFevr3zw4AEaNWokt65Ro0afnI1s0KDBJ4+/dMYyICAAycnJsuXFixcFyv058wfWxdL9d/DH+We4F/0Wv5+NwurQe5jQ3e2z2zyPT0VC8js4WRrIrS9vrI0js9rh0qN4jPxJsb92NTU1haqqKuLj5e8kjo+L++SDhLJxdHLCsZOnEZ+YiodR0Th7/jI+ZGfD3sFR7GiFoqGhAScnZ9Sq7Y5Zc+ajWvUaWLdmJcwtLZGVlYWkpCS59gnxcbCwUO6xMzIygnPFSnj65InYUQThN2YUDh8OxbET4bC2thY7TqHZOzhhT+hJPHrxBpF3nuDQyQh8yP4AW3sHRF48j9cJ8fBwqwg7M13Ymeni7xfRCJw+GfVrVBI7eqGUxePhtIBJGD9hMnr17otq1arjm/4DMWqMH5b++OVvLxWdoo+VwheWVlZWuHnzpmwZPnw4gLyvnS9evIiGDRti586dqFSpEi5d+vfaKnV1dbn9SCQSSKXSL76Wrq5ugTIdOXIErq6usLGxKWRvhKGpqQkDAwO5pTi0NdUglcpPv5AjzYXKFz6BVzDRQTl9LcS+zZCtszLRwdHZ7XHj6Rt8t+YcFH1GBw0NDdSq7Y7wU2GydVKpFOHhYahXv8EXtlQeurq6KF++PN6+fYuTJ46hYyflvtlMKpUiKzMTNWu5Q11dHWfC/x27x48e4sWLaNTzqC9iwuJLS0vDs6dRsCxfXuwoxZKbmwu/MaMQcmAfjh4/Bfv/XbOurHR0dWFhWR5JSW9x5tQJtGnXET36fIMT567i2JlI2WJR3grDR/vjtz9CxY5cKGXxePguIwMqKvJljoqq6ldrAUWn6GOl8F+Fq6mpwdnZOd/natWqhVq1aiEgIAANGjTA9u3bUb++cH9UNDQ0AOTdOPBf//0a/B/q6uqftKtSpQrOnz+PwYP/PeV+/vx5uLrKX+B96dIlDBo0SO5xrVq1BOlDQRy++gKTetTAi9dpuP8iCTUdymF0x6rYFv4YAKCrpYapvWph/6XniEt6B0dLfcwbUBdRsSk4cTNvyo28orIdohPSMXVbJMwM/r1xJC7pXan1pbDG+PnD12cw3N3roE7deli9MggZ6ekYNHiI2NGK5cTxY8jNzUWlSi6IinqCaQGTUMmlMgYqUb9mTZ+K1m29YG1ji7TUVOze+Tsizp7G3oNHYGhoiIHePpg2eQKMTUygr2+ASf5jUc+jAeoqWWEZMHkC2nfoBFtbO8TEvMLcwFlQVVVFrz79xI5WLH6jR2Lnju3YvfcA9PT1Zdd+GRoaQltbW+R0BXc67ARyc3PhVLEinj+NwtyZU+FU0QV9+g+Guro6jE3KybVXV1ODubkFnCoq1xlLoOwdD9t16IQfF82HjY0tqrhWxa1bN7B6xXKlOg5+jiKPlcIXlvl59uwZNmzYgM6dO8PKygoPHz7E48eP5YozIZibm0NbWxtHjx6FtbU1tLS0oKuriyNHjnwyBZK9vT3CwsLQqFEjaGpqwtjYGBMnTkTv3r1Rq1YttGrVCgcPHsTevXtx8uRJuW13796NOnXqoHHjxvjtt98QGRmJTZs2CdqXLxm/6SJm9HVHkG9DmBloIeZtBjafeIj5f9wEkHf2spqdMfo3d4aRjgZi3mYg7NYrBO64hqwPeZ/8PN2s4FzeEM7lDfFkQ1+5/ev0FH/6g8/p1bsPXickIHD2DMTFxsKtRk0cCD0KCwuLr2+swFJSkjHzh6l4+fJvGJuYoGvX7pgZOO+TM/mKLCEhHsO/9UZsbAwMDA1RtZob9h48As+WrQEAC35cBhUVFQzs1wtZmZnwbNUGy1asETl14b38+yUGD/wGiW/ewNTMDA0bNsbpcxdl124rqw0/5U1t1aZlc/n1G7dg4GDv0g9URKkpyVg4ZzpiXr2EkbEJ2nXqisk/zFaq91JBlbXj4dLlKxE4azr8xo5EQnw8ype3gs/QYQiYNkPsaMWmyGMlyVWwKeiDg4Ph5+f3ybVT/xUXF4fhw4fj8uXLePPmDcqXL4/Bgwdj5syZUFFRwaxZs7B//365ic2DgoIQFBSE58+fA8ibbqhmzZoICgoCkFcY+vn5ffK/8WzcuBGBgYF4+fIlmjRpgunTp8Pb2/uT6xoPHjwIf39/PH/+HBUqVJC9zrp167BkyRK8ePECDg4O+OGHHzBw4EDZdhKJBGvWrMH+/ftx9uxZlC9fHosWLULv3r0L/DNLSUmBoaEhtDqvhkRdec4EFETiDh+xI5SIjy89KCs+lNF+qauWvRszyurNJm9SFXeKs+Iop//l6d2UVVk9Fn5uxhRllpKSAotyhkhOTv7iJXgKV1gqujFjxuDDhw+fvWO7sCQSCfbt24euXbsWeR8sLJVPWT2YsrBUHiwslQsLS+Xy/7mwVMqvwsVUrVq1T+7iJiIiIiIWloU2bNgwsSMQERERKSQWliLjlQhERERUVij8PJZEREREpBxYWBIRERGRIFhYEhEREZEgWFgSERERkSBYWBIRERGRIFhYEhEREZEgWFgSERERkSBYWBIRERGRIFhYEhEREZEgWFgSERERkSBYWBIRERGRIFhYEhEREZEgWFgSERERkSBYWBIRERGRIFhYEhEREZEgWFgSERERkSBYWBIRERGRINTEDkDCeb55AAwMDMSOISjjhuPFjlAiEs8vETtCiZCIHaCESCRltWdlTzl9TbEjUCGoqPC9VdbwjCURERERCYKFJREREREJgoUlEREREQmChSURERERCYKFJREREREJgoUlEREREQmChSURERERCYKFJREREREJgoUlEREREQmChSURERERCYKFJREREREJgoUlEREREQmChSURERERCYKFJREREREJgoUlEREREQmChSURERERCYKFJREREREJgoUlEREREQmChSURERERCYKFJREREREJgoUlEREREQmChSUV2pIfF0JHQwUTx/uJHeWL9HQ0sXhcFzw8MA2JZxcifONouFexkWvjYm+O3Ut8EHtqLl6fmY+I4LGwsTCSPe/TtT6OrRuBuFPz8C5yKQz1tEq5F8WnLOP1saWLF6JZIw9YmRnC0dYS/Xp1w+NHD/Ntm5ubi+5d2sNAWxWhIftLN2gxbVi/DnVrucHcxADmJgZo1rgBjh09InYswaxfuwYuzvYw0tNCk4YeuBIZKXakYlm8aAEa1a8LM2N92FqZo1ePrnj0MP/fS2XE8VIeijpWZbKwlEgkX1xmzZoldkSldfXqFWzauAHVq7uJHeWr1k3rDU+PSvCZ9TvqfLMYJy8/xKE138HKzAAA4FChHMJ+HoVHf8Wj7fB1qPvNUizYdBLvsz7I9qGjpY4TFx9icXCYWN0oFmUar49FnDuDYcNHIOzMBRwIPYbsD9no2tEL6enpn7Rds2oFJBKJCCmLr4K1NebMX4gLl6/h/KWraN7CE726d8H9e/fEjlZsu3ftxOSJ/pj2w0xcjLwON7ca6NyhLeLj48WOVmTnzp7B8BEjcSbiEkKPnMCH7Gx0bN8m399LZcPxUh6KPFaS3NzcXLFDCC02Nlb27507d2LGjBl4+J9PKHp6etDT0wOQd6YjJycHampqpZ7za7KysqChofHVdikpKTA0NETs6yQYGBiUWJ60tDQ0rOeOoFVrsGjBPLjVqIHFS4NK7PUAwKTRhCJtp6WphoTw+eg1cQuOnn8gW39+qx+OX/wTs9cfxba5A5D9IQffzvr9q/trUtsJx9d/D0vPaUhOe1+kTP+VeH5JsffxNWKM14eckjucvE5IgKOtJY6cCEejxk1l62/fuone3TvjzPlIVHSogO0796Bj566Cvra6Wul+BrcyN8H8hYvh7fNtqb6u0Jo09IB7nboIWrkaACCVSuHsYIMRI0dj4qQpIqcTRkJCAmytzHHi1Bk0btL06xsoMI6X8hBjrFJSUmBRzhDJyclfrDXK5BlLS0tL2WJoaAiJRCJ7/Oeff0JfXx9HjhyBu7s7NDU1ERERgczMTIwZMwbm5ubQ0tJC48aNceXKFdk+g4ODYWRkJPc6+/fvlztLcuvWLbRo0QL6+vowMDCAu7s7rl69Kns+IiICTZo0gba2NmxsbDBmzBi5T0329vaYM2cOBg0aBAMDAwwbNqzkfkhFMG7MKHi1bw/Plq3EjvJVaqqqUFNTlTv7CADvMz+gYQ0HSCQSeDWqgsfRCQhZOQx/HZ2Fs5vHoFOzaiIlFp4yjVdBJKckAwCMjU1k6zIyMvCt9wAsDVoFC0tLsaIJJicnB7t27kB6ejo86jcQO06xZGVl4cb1a3K/fyoqKvD0bIXISxdFTCaslORPfy+VEcdLeSj6WJXJwrIgpkyZgoULF+LBgwdwc3PDpEmTsGfPHmzduhXXr1+Hs7Mz2rZti8TExALvs3///rC2tsaVK1dw7do1TJkyBerq6gCAqKgoeHl5oUePHrh9+zZ27tyJiIgIjBo1Sm4fS5YsQY0aNXDjxg1Mnz4939fJzMxESkqK3FLSdu/cgZs3riNw7oISfy0hpGVk4tLt5wjwaYXypgZQUZGgr1dteFS3g6WpAcxN9KCvq4UJgz1x4uKf6DR6A0JO38WORYPRuJaj2PGLTdnG62ukUimmTByH+g0awbXqv8V/wCR/eNRvgA6duoiYrvju3rkDUyM9GOpqYszI4dj5xz5UcXUVO1axvH79Gjk5OTA3t5Bbb25hIfetkjKTSqWYON4PDRo2QtVqyv2hlOOlPBR9rBTv+99SEhgYiNatWwMA0tPTsW7dOgQHB6Ndu3YAgJ9//hknTpzApk2bMHHixALtMzo6GhMnTkTlypUBABUrVpQ9t2DBAvTv3x9+fn6y51auXIlmzZph3bp10NLKuynE09MT48eP/+LrLFiwALNnzy5Uf4vj7xcvMHG8Hw4ePi7LqQx8Zm7HT9P74OnhmfjwIQc3H77EruM3UKuyNVT+d6Y59Ow9rPr9LADg9uNX8HCzh2/3hoi48VTM6MWirOP1JeP9RuHBvXs4FnZWtu5waAjOnA5HxKVrIiYTRiUXF1y+ehPJycnYt/cP+PoMxvGwM0pfXJZ1fqNH4t69uwg7HSF2FCoAjlfp+H97xrJOnTqyf0dFRSE7OxuNGjWSrVNXV0e9evXw4MGD/DbPl7+/P4YOHYpWrVph4cKFiIqKkj1369YtBAcHy67v1NPTQ9u2bSGVSvHs2bN8c31OQEAAkpOTZcuLFy8KnLEorl+/hvj4eDT0cIe+tjr0tdVx7uwZrF29Cvra6sjJySnR1y+qZy/foM3wtSjXNAAVO81BkyEroK6mimcv3+B1UjqyP+TgwbM4uW0ePo+DjaWROIEFoqzj9Tnj/Ubj6OFDCD0WhgrW1rL1Z06H49nTKNhYmsBYTwPGennXIw/o1wvt23iKFbdINDQ04OTsjNru7pgzbwGqu9XAmlUrxI5VLKamplBVVUV8vPx7LD4uDpZl4LIFvzGjcPhwKI6dCIf1f34vlRXHS3ko+lj9vy0sdXV1C9VeRUUFH9/nlJ2dLfd41qxZuHfvHjp06IBTp07B1dUV+/btA5B3I8V3332HmzdvypZbt27h8ePHcHJyKlQuTU1NGBgYyC0lqYVnS1y5fhuXrtyQLbXd66Bvv/64dOUGVFVVS/T1iyvjfRZi36TCSF8breq7IPTsPWR/yMG1+y9QydZMrm1FWzNEx74VKakwlH28/pGbm4vxfqMRGrIfB4+ehL29g9zz/hMm4+KVmzh/+bpsAYAFPy7D2g2bxIgsGKlUiszMTLFjFIuGhgZq1XZH+Kl/Z1SQSqUIDw9DPSW+fjQ3Nxd+Y0Yh5MA+HD1+CvYODl/fSAlwvJSHoo/V/9uvwv/LyckJGhoaOH/+POzs7ADkFY1XrlyRfXVtZmaG1NRUpKeny4q/mzdvfrKvSpUqoVKlShg3bhz69euHLVu2oFu3bqhduzbu378PZ2fn0uqWYPT19T+5HkVXVxcm5UwU+jqVVvVdIAHwKDoBTtammD+mIx49j8e2g3lzfS3/NRy/zBuIiBtPcebaE7RpUBntG7ui7Yh1sn1YlNOHhYk+nGxMAQDVnMsjNT0TL+Le4m3KOzG69VXKOl4f8/cbhT92/o7fd++Dvp4+4v537ZCBoSG0tbVhYWmZ7w07NjY2nxShimz6tAC09WoHGxtbpKamYueO7Th75jQOHj4mdrRiG+PnD1+fwXB3r4M6deth9cogZKSnY9DgIWJHKzK/0SOxc8d27N57AHr6+rJr2gz/93upzDheykORx4qFJfL+6I4YMQITJ06EiYkJbG1t8eOPP+bdcfpt3nQfHh4e0NHRwdSpUzFmzBhcvnwZwcHBsn28e/cOEydORM+ePeHg4IC///4bV65cQY8ePQAAkydPRv369TFq1CgMHToUurq6uH//Pk6cOIHVq1eL0e0yz1BPC4Hft0cFcyMkpmTgwKnbmLnuCD7kSAEAIafvYvTCPZg42BNLx3fDo+h49JuyFRdu/XtpwtDuDfCDb1vZ45Mb8m628p29A78eugIqOZs2rAeAT77WXrdhE/oP9BYhUclIiI/Ht0MGITYmBoaGhqhW3Q0HDx9Dy1atxY5WbL1698HrhAQEzp6BuNhYuNWoiQOhR2FhYfH1jRXUhp/yPni2adlcfv3GLRg42Lv0AwmI46U8FHmsyuQ8lv8VHBwMPz8/JCUlAQBOnz6NFi1a4O3bt3LTB71//x6TJk3C77//jtTUVNSpUwfLly9H3bp1ZW3279+PiRMn4uXLl2jZsiU6d+6MYcOGITc3F1lZWRg8eDDOnz+PuLg4mJqaonv37li8eLHsBoorV65g2rRpuHjxInJzc+Hk5IQ+ffpg6tSpAPKmG/Lz85OdJS2o0prHUgxFncdS0ZXGPJZiKMl5LMVU2vNYEhEpmoLOY1nmC8v/D1hYKh8WlsqFhSUR/X/3/3qCdCIiIiIqfSwsiYiIiEgQLCyJiIiISBAsLImIiIhIECwsiYiIiEgQLCyJiIiISBAsLImIiIhIECwsiYiIiEgQLCyJiIiISBAsLImIiIhIECwsiYiIiEgQLCyJiIiISBAsLImIiIhIECwsiYiIiEgQLCyJiIiISBAsLImIiIhIECwsiYiIiEgQLCyJiIiISBAsLImIiIhIECwsiYiIiEgQamIHIOFIc/OWsuTthaViRygRVSYeEjtCibi3qL3YEUrEizcZYkcQnE05HbEjlIg3aVliRygR5fQ0xI5AVCA8Y0lEREREgmBhSURERESCYGFJRERERIJgYUlEREREgmBhSURERESCYGFJRERERIJgYUlEREREgmBhSURERESCYGFJRERERIJgYUlEREREgmBhSURERESCYGFJRERERIJgYUlEREREgmBhSURERESCYGFJRERERIJgYUlEREREgmBhSURERESCYGFJRERERIJgYUlEREREgmBhSURERESCYGFJRERERIJgYfk/9vb2CAoKkj2WSCTYv3+/aHnEFHHuLHp16wxn+wrQ01TBwQP75Z6fN2cWalWvAnNjPVhbmKCjV2tcibwsTthiWLxoARrVrwszY33YWpmjV4+uePTwodixvurc9BZ4trzDJ0tgj6qftN0yrC6eLe+A1tUs5NZbGWlhk29d3F/khSuBrRDQqTJUVSSl1YUiS01NxcTxfqhc0R7lDHXg2awRrl29InasL7pyMQLfDeyJxjWcUMlSFyeOHPxs2xmTxqCSpS6CN6zO9/mszEx0blkflSx1cf/urZKKLKj1a9fAxdkeRnpaaNLQA1ciI8WOVChpqamYGTAeHtUrwqm8Ibq0aYab16/Kns/NzcXi+bNRu7IdnMobom9XLzyNeixi4uJR9vH6mLIe5wtCUceqzBSW3t7ekEgkkEgk0NDQgLOzMwIDA/HhwwexoymdjPR0VHNzw7IV+f9xq1ixEpYFrcLla7dxPPwc7Ozt0KVDWyQkJJRy0uI5d/YMho8YiTMRlxB65AQ+ZGejY/s2SE9PFzvaF3VZdh51Z5yULQPWXQIAHLoZI9fOp5kDcnM/3V5FAmzyrQsNVQl6rLiACdtvoUc9a4zzqlQa8Ytl5HBfhIedxMbN2xB57TZatmqNju1a49XLl2JH+6yMjHRUrlodMxYs/2K744dDcPNaJMwty3+2zY9zpsHc4vPPK5rdu3Zi8kR/TPthJi5GXoebWw107tAW8fHxYkcrsIljh+Pc6TCsWL8ZJ89fQ1PPVujXtR1iXuX9zq1dsRRbflqDBctW4eCJCOjo6GJAj454//69yMkLryyM18eU9Tj/NYo8VmWmsAQALy8vxMTE4PHjxxg/fjxmzZqFxYsXix2ryLKyskR53TZe7TBz9lx07tIt3+d79/0GLVq2goOjI1xdq2LBj8uQkpKCu3dul3LS4gk5dBQDB3vDtWpVuNWogQ2bgvEiOho3rl8TO9oXJaZn4XVqpmzxdLXA84R0XI5KlLWpYmWAoc0dMGnHp2PSxMUMFS31Me7Xm3jwKgVn/kzAsiOPMLCxHdRVFfes5bt377B/3x7Mnb8IjZs0hZOzM6ZNnwVHJ2f8vGGd2PE+q1nLthg3ZSbatO/82TaxMa8wZ9p4LF2zGepq6vm2ORN2DBFnTmHKzPklFVVwK4OWYci3vhjkPQRVXF2xau16aOvoYGvwZrGjFci7d+9wOGQfps2aj/qNmsDB0Rnjp0yHvaMTftm8Abm5udi0fhXGTJiCtu07w7VadQSt24y42BgcOxQidvxCU/bxyo+yHue/RpHHqkwVlpqamrC0tISdnR1GjBiBVq1aISQkBM2bN4efn59c265du8Lb27vA+75z5w48PT2hra2NcuXKYdiwYUhLSwMAHD9+HFpaWkhKSpLbZuzYsfD09JQ9joiIQJMmTaCtrQ0bGxuMGTNG7lOTvb095syZg0GDBsHAwADDhg0r9M+gtGVlZWHLxg0wNDREdbcaYscplpTkZACAsbGJyEkKTl1Vgq7uFbA78oVsnZa6ClYMrImZe+7hdWrmJ9vUtjfGw5gUvE7794PL2T8TYKCtjoqW+qWSuyg+fPiAnJwcaGppya3X1tbGxQvnRUpVfFKpFJNGfYuh3/uhYmXXfNu8TojDDxNGYfGqjdDS1inlhEWTlZWFG9evwbNlK9k6FRUVeHq2QuSliyImK7icz/zOaWlpI/LSBUT/9QzxcbFo0ryl7DkDQ0PUdK+Ha1culXbcYikL41UQynic/5iij1WZKiw/pq2tLchZv/T0dLRt2xbGxsa4cuUKdu/ejZMnT2LUqFEAgJYtW8LIyAh79uyRbZOTk4OdO3eif//+AICoqCh4eXmhR48euH37Nnbu3ImIiAjZPv6xZMkS1KhRAzdu3MD06dPzzZOZmYmUlBS5pbQdORQKCxN9lDPQxupVQQg5fBympqalnkMoUqkUE8f7oUHDRqharZrYcQqsTXVLGGir4Y/Iv2Xrpnd1xfXnb3Hibly+25gZaOJ1qvz74p8C1Exfs+TCFpO+vj486jfAogVzEfPqFXJycvD79l9x+dJFxMbEfH0HCmrD6qVQVVPDoKHf5/t8bm4uJo/5Dv0GDUX1mrVLOV3RvX79Gjk5OTA3l7++19zCArGxsSKlKhw9fX24162PoMULEBuT9zu3Z+d2XLtyCfFxMUiIy3uPmZqZy21nZm6OhPj833+KqiyM19co63H+Y4o+VmWysMzNzcXJkydx7NgxuTOGRbV9+3a8f/8e27ZtQ7Vq1eDp6YnVq1fjl19+QVxcHFRVVdG3b19s375dtk1YWBiSkpLQo0cPAMCCBQvQv39/+Pn5oWLFimjYsCFWrlyJbdu2yV2L4+npifHjx8PJyQlOTk755lmwYAEMDQ1li42NTbH7WFhNm7fAhcgbCDtzHq3btMWgb/ooxLUdReU3eiTu3buLbb/tEDtKofT2sMGZPxMQn5JXGLaqao4GFU0RuO++yMlKxsbN25CbmwtnB2sY62th3ZpV6NWnH1RUlPNQdvfWDWz7eS0WrtgAiST/yxB+2bQO6elp+G7MhFJORwCw4qfNyM3NRR1XBzha6GPzhjXo0qOP0v7O/X+mrMd5ZVOm3hmhoaHQ09ODlpYW2rVrhz59+mDWrFnF3u+DBw9Qo0YN6OrqytY1atQIUqkUD/93d1n//v1x+vRpvHr1CgDw22+/oUOHDjAyMgIA3Lp1C8HBwdDT05Mtbdu2hVQqxbNnz2T7rVOnzlfzBAQEIDk5Wba8ePHiq9sITVdXF07OzqjnUR9rf9oENTU1bAveVOo5hOA3ZhQOHw7FsRPhsLa2FjtOgVUw1kajSqbYeenf8W9Q0RR25XRwa34bPF7SDo+XtAMArBvijt9H1gcAJKRkwlRfQ25fpv87U5mQz1fnisTRyQnHTp5GfGIqHkZF4+z5y/iQnQ17B0exoxXJ1cvn8eZ1Apq7u6BKBQNUqWCAl39HY+GsALSoUwUAcDHiDG5evYxqtsaoUsEArRtUBwD0aNsEk0b7ihn/i0xNTaGqqor4j87cxcfFwdLSUqRUhWfv4IQ9h07i0d+JiLwbhUNh5/HhQzZs7RxgZpF3xuh1gvyH6oT4eJh9dDZJ0ZWV8focZT3O50fRx0pN7ABCatGiBdatWwcNDQ1YWVlBTS2veyoqKsj96PbY7OxsQV+7bt26cHJywo4dOzBixAjs27cPwcHBsufT0tLw3XffYcyYMZ9sa2trK/v3f4vXz9HU1ISmpmJ9ZSmVSpGZqdhFycdyc3MxbuxohBzYh+MnT8PewUHsSIXSs5413qRl4tT9f/+orQuLws5L0XLtjk1uhrn77+PkvbyD0PXnbzGytTPK6Wngzf+us2ziYoqUd9l4EptWeh0oBl1dXejq6uLt27c4eeIY5s5fJHakIunSsx8aNmkht86nXxd06dkPPfoOBABMn7sE4ybPkD0fHxcDn75dEPTTNtSoXbdU8xaGhoYGatV2R/ipMHTu0hVA3nEiPDwMw78f9eWNFZCOri50dHWRlPQWZ8JOYOrs+bC1c4C5hSUizpxC1ep515inpqTg5rVIDPJR/Gvk/6usjdc/lP04nx9FH6syVVjq6urC2dn5k/VmZmaI+c81WDk5Obh79y5atGjxSdv8VKlSBcHBwUhPT5cVfufPn4eKigpcXFxk7fr374/ffvsN1tbWUFFRQYcOHWTP1a5dG/fv3883n6JJS0vD06gnssd/PX+G27duwtjYBCblymHxwnlo37EzLC3L482b19iwfg1evXqJbj16iZi68PxGj8TOHduxe+8B6Onry65NMTQ0hLa2tsjpvkwiAXrVs8aeK38jR/rvh6Z/7hT/2Mu37/B34jsAwLmHCXgcm4pl/Wti4cEHMNPXhH87F/wS8ReycqSl1oeiOHH8GHJzc1Gpkguiop5gWsAkVHKpjIGDh4gd7bPS09Pw17Mo2eO/o5/j/t1bMDIygZW1DYxNysm1V1dTh5m5BRyd86Z/srKWv9RFR1cPAGBj7wBLqwolnL54xvj5w9dnMNzd66BO3XpYvTIIGenpGKTA4/Wx02HHkZubC6eKlfD8aRTmzgiAUyUX9Ok/GBKJBN8OH42VSxbCwdEZNnYOWDJ/Fiwsy6Nth8/PAqCoysJ4fUyZj/NfoshjVaYKy8/x9PSEv78/Dh06BCcnJyxbtuyTO7i/pH///pg5cyYGDx6MWbNmISEhAaNHj8bAgQNhYWEh127WrFmYN28eevbsKXdWcfLkyahfvz5GjRqFoUOHQldXF/fv38eJEyewenX+80WK5fq1q2jf5t9rU6dMGg8A6D9wMFasXoeHDx/it1974s3r1zApVw7u7nVx/NRZuLp+OkG3ItvwU94UNW1aNpdfv3ELBg72Lv1AhdC4kikqmOhg9+W/v974I9JcYOjGq5jTsxr2jG2EjKwP2HvlJZYffVQCSYWVkpKMmT9MxcuXf8PYxARdu3bHzMB5UFfPf4oeRXD35nUM7NFO9njBzCkAgG69+2PRyg1ixSoVvXr3weuEBATOnoG42Fi41aiJA6FH5Y6bii41JQULA39AzKuXMDI2QbtOXTH5h0DZ79z3Y8cjIyMdk8eNREpyEurWb4hf/zgIrY/uJFcGZWG8PqbMx/kvUeSxkuR+/B2xkvL29kZSUlK+/1tOdnY2xo4di507d0JNTQ3jxo3DpUuXYGRkJPu62t7eHn5+frJpiSQSCfbt24euXbsCyJtuaOzYsbh48SJ0dHTQo0cPLFu2DHp6enKv5eHhgcjISJw6deqTM6JXrlzBtGnTcPHixbxPwE5O6NOnD6ZOnZpvhoJKSUmBoaEhXiUkwcDAoFDbKjpl+N9giqLKxENiRygR9xa1FztCiXj59p3YEQRnU045pi0qrDdp4sz/W9LK6Wl8vRFRCUpJSYFFOUMkJyd/sdYoM4Xl/2csLJUPC0vlwsJSebCwJCoZBS0sy9Rd4UREREQkHhaWRERERCQIFpZEREREJAgWlkREREQkCBaWRERERCQIFpZEREREJAgWlkREREQkCBaWRERERCQIFpZEREREJAgWlkREREQkCBaWRERERCQIFpZEREREJAgWlkREREQkCBaWRERERCQIFpZEREREJAgWlkREREQkCBaWRERERCQIFpZEREREJAgWlkREREQkCBaWRERERCQINbEDkHByc3ORm5srdgxBlbHuyNz/sb3YEUqESYelYkcoEbEHxokdgQpIT1NV7AhE/6/xjCURERERCYKFJREREREJgoUlEREREQmChSURERERCYKFJREREREJgoUlEREREQmChSURERERCYKFJREREREJgoUlEREREQmChSURERERCYKFJREREREJgoUlEREREQmChSURERERCYKFJREREREJgoUlEREREQmChSURERERCYKFJREREREJgoUlEREREQmChSURERERCYKFJREREREJgoUlEREREQmChSV9YsmPC9GskQfKmxrCwcYSfXt1w6NHD+XavH//Hv5jR8HWygyW5QzQv29PxMfFiZS4aOYGzoKOhorcUrNaFbFjFVvlig6f9EtHQwV+Y0aKHe2L9LTVsXh4Czz8ZRgSD45F+PJ+cK9kKddm+qBGePr7cCQeHItDC3vBycpI9pythQHW+bfFg22+SDw4FveCh+KHgQ2hrqZYh7lNG9ajYb1asLEwho2FMVo3b4QTx4580i43Nxc9u3SAkY4aQkMOiJBUGOvXroGLsz2M9LTQpKEHrkRGih2pwL40Vm8TEzHRfyzq1HCFpYkeqlVywKTxfkhOThY5dfEo83h9TlnsE6C4/VKsI66IvL29IZFIIJFIoK6uDgsLC7Ru3RqbN2+GVCoVO16pOn/uDHy/G4FTZy8g5NAxZGdno2sHL6Snp8vaTJnojyOHQvHLbztx5EQ4YmJi8E2fniKmLhpX16p4Gv1Ktpw8fU7sSMV27kKkXJ9CjxwHAHTv0UvkZF+2blxbeNa2g8+Ph1Hnu604ef0vHFrUC1bl9AAA43vXw/dda2HMyhNoOuY3pL/PxsEFPaGprgoAcLExgYpEglErjqO2bzAmrQ/H0I41EDikiZjd+oRVhQqYFTgPp89HIjziMpo2a4FvenfHg/v35NqtXb0CEolEpJTC2L1rJyZP9Me0H2biYuR1uLnVQOcObREfHy92tAL50ljFxLxCbMwrzJm/CBev3sKaDZsQduIYRo/wFTt2kSn7eOWnLPYJUOx+SXJzc3PFDqEIvL29ERcXhy1btiAnJwdxcXE4evQoFixYgCZNmiAkJARqamqfbJednQ11dXUREv8rJSUFhoaGeBn/FgYGBoLvPyEhAY42ljhyIhyNmzRFcnIyHKwtsHnrr+jaPa+YfPjwT9SpURVhZ86jnkd9wV5bVaXk/rDODZyFgyEHcPnqjRJ7DUUwcbwfjhw+hDv3H5V4oWLSYWmRttPSUEPCgTHoNXM/jkY+la0/v2YAjl95htnB5/H09+FYuecqgv64CgAw0NHAX7u+x7AlR7D79MN89zuuV134dqwB18Ebi5TrH7EHxhVr+6+xr2CGwHmLMMjbBwBw+9ZN9O3RBeERl+HiaI1fd+xBx85dBH3NfwryktSkoQfc69RF0MrVAACpVApnBxuMGDkaEydNKZHXzMzOKZH9/uPjsfqv/Xv/wDCfQXj1OiXfvxfFUVbHq6SVxT4B4vQrJSUFFuUMkZyc/MVag2cs/0NTUxOWlpaoUKECateujalTp+LAgQM4cuQIgoODAQASiQTr1q1D586doauri3nz5gEADhw4gNq1a0NLSwuOjo6YPXs2Pnz4ACDvK61Zs2bB1tYWmpqasLKywpgxY2Svu3btWlSsWBFaWlqwsLBAz56KdeYvJSXvqx0TExMAwM3r15CdnY3mnq1kbVxcKsPGxhaRly+JkrGoop48hqNdBbi6OGHIoAF4ER0tdiRBZWVlYcf23zBo8BCFPvulpiqBmqoK3md9kFv/PvMDGla1hr2lIcqX08Op63/JnkvJyMKVP2PgUcXqs/s10NVAYur7EstdXDk5Odizeycy0tNlH8gyMjLgO2QgFi9fBQtLy6/sQXFlZWXhxvVr8Gz573FCRUUFnp6tEHnpoojJiia/sfpYSnIy9A0MBC8qS0NZGy+gbPYJUPx+Kd9vfynz9PREjRo1sHfvXgwdOhQAMGvWLCxcuBBBQUFQU1PDuXPnMGjQIKxcuRJNmjRBVFQUhg0bBgCYOXMm9uzZg+XLl2PHjh2oWrUqYmNjcevWLQDA1atXMWbMGPzyyy9o2LAhEhMTce7cl7+OzczMRGZmpuxxSkpKCfU+71PQ5AnjUL9BI7hWrQYAiIuLhYaGBoyMjOTamltYIC4utsSyCK1uPQ9s2LgFFSu5IDY2BvPnBqKVZ1NcvXEH+vr6YscTxMED+5GUlIQBg7zFjvJFae+yceneSwT0b4CH0W8Ql5SB3i0qw6OKFaJeJcHSRBcAEJ+UIbdd/NsMWBjr5rtPRysjjOhSGwEbTpd0/EK7d/cO2rRojPfv30NXTw+/7vgDlau4AgCmThqPeh4N0KFTZ5FTFs/r16+Rk5MDc3MLufXmFhZ4+PBPkVIV3pfG6r/evH6NHxfOg/eQoSKkLL6yMl7/VRb7BCh+v1hYFkDlypVx+/Zt2eNvvvkGQ4YMkT328fHBlClTMHjwYACAo6Mj5syZg0mTJmHmzJmIjo6GpaUlWrVqBXV1ddja2qJevXoAgOjoaOjq6qJjx47Q19eHnZ0datWq9cU8CxYswOzZs0ugp5/yHzsKD+7dw/FTZ0vl9UpTW692sn9Xd3ND3XoeqOxsjz1/7IL3kG9FTCacrcGb0aZtO1hZff6snqLw+fEwfhrvhac7RuBDjhQ3H8dh1+k/Uauixdc3/ohVOT2EzOuBvWcfYsuROyWQtngqVnLBuUvXkJKcjAP792DEMB8cOnYKT6OicPZMOM5evCp2RPqfz43Vf4vLlJQU9O7eCZUrV8GUH2aKmJZIfCwsCyA3N1fua8Q6derIPX/r1i2cP39e9rU4kPe1yfv375GRkYFevXohKCgIjo6O8PLyQvv27dGpUyeoqamhdevWsLOzkz3n5eWFbt26QUdH57N5AgIC4O/vL3uckpICGxsbAXucZ7zfaBw9fAhHT55GBWtr2XoLC0tkZWUhKSlJ7qxlfFwcLCyU96s7IyMjOFeshKdPnogdRRDRf/2FU2En8fuuPWJHKZBnMcloM2EndLTUYaCjgdjEdPwytSOexSQjNjHvxjFzIx3ZvwHA3FgHt6PkL1Yvb6KLo4t749L9VxgZdLxU+1BQGhoacHRyBgDUrO2O69euYv2aVdDS1sazp1GwK19Orv2gb3qhQaPGOHTslBhxi8TU1BSqqqqIj5efLSI+Lg6WSvQV/+fGKmj1OgBAamoqenZpDz19ffy6c4/o19wXVVkZr/8qi30CFL9fvMayAB48eAAHBwfZY11d+a/e0tLSMHv2bNy8eVO23LlzB48fP4aWlhZsbGzw8OFDrF27Ftra2vj+++/RtGlTZGdnQ19fH9evX8fvv/+O8uXLY8aMGahRowaSkpI+m0dTUxMGBgZyi5Byc3Mx3m80DobsR+ixk7D/T9+BvIOruro6zoSHydY9evQQL15EC3rjTmlLS0vDs6dRsCxfXuwogti2dQvMzM3Rrn0HsaMUSsb7bMQmpsNITxOt6tgj9OITPI9NRsybNLSoZSdrp6+jgbqVy+Pyg1eydVbl9HBsSR/ceByHYUuPQlluTZRKpcjMysS48ZNwPvIGzl26JlsAYP6PS7Hmp00ipywcDQ0N1KrtjvBT/x4npFIpwsPDUK9+AxGTFc8/YwXkfajv3skL6hoa+H33fmhpaYmcrujK4niVxT4Bit8vnrH8ilOnTuHOnTsYN+7zd4XWrl0bDx8+hLOz82fbaGtro1OnTujUqRNGjhyJypUr486dO6hduzbU1NTQqlUrtGrVCjNnzoSRkRFOnTqF7t27l0SXvsp/7Cjs3vk7duzeB309fcTF5l03aWBoCG1tbRgaGmKQtw8CJk2AsbEJ9A0MMMF/LOrVb6BUhWXA5Alo36ETbG3tEBPzCnMDZ0FVVRW9+vQTO1qxSaVS/LItGAMGDFKaGwlaudtDIgEe/f0WTlZGmO/bDI9eJGLbsbsAgDX7rmPyN/Xx5OVbPI9NxkzvRoh5k4aQ83lnmP8pKqPjUhCw4QzMDLVl+457m5Hva4ph9oypaNXGC9Y2tkhLTcUfu35HxNkz2BtyGBaWlvnesGNtbQt7e4d89qbYxvj5w9dnMNzd66BO3XpYvTIIGenpGDR4yNc3VgBfGqt/isqMd++wYfM2pKakIPV/17ubmplBVbXk7+IWmrKPV37KYp8Axe6XcvzFKSWZmZmIjY39ZLqhjh07YtCgQZ/dbsaMGejYsSNsbW3Rs2dPqKio4NatW7h79y7mzp2L4OBg5OTkwMPDAzo6Ovj111+hra0NOzs7hIaG4unTp2jatCmMjY1x+PBhSKVSuLi4lGLP5W3csB4A0K6Np9z6dRs2yW4CWbh4GVRUVDCgXy9kZmaiZes2WL5iTWlHLZaXf7/E4IHfIPHNG5iamaFhw8Y4fe4izMzMxI5WbKfCTuJFdHS+U6IoKkNdTQT6NEEFUz0kpr7HgYjHmLnlHD7k5M0ju3RXJHS01LHarw2M9DRx4e5LdJ66Rza9jGdtOzhXMIZzBWNE/T5cbt/abZaUen8+JyE+AcOHDkFcbAwMDA1RtVp17A05jBYtW4sdTXC9evfB64QEBM6egbjYWLjVqIkDoUdhYVH462bF8KWxOnf2NK5eyZuQulY1+eP1rQdPYGdnL0Li4lH28cpPWewToNj94jyW/+Pt7Y2tW7cCANTU1GBsbIwaNWrgm2++weDBg6GiknfVgEQiwb59+9C1a1e57Y8dO4bAwEDcuHED6urqqFy5MoYOHQpfX1/s378fCxcuxIMHD5CTk4Pq1atj7ty5aNmyJSIiIvDDDz/g9u3beP/+PSpWrIhp06ahd+/eBc5e0vNYiqkk57Ek4RV1HktFV9LzWIqhNOZFFENJz2MplrI6XqQ8CjqPJQvLMoCFJSkKFpbKo6wWKiwsiUoGJ0gnIiIiolLFwpKIiIiIBMHCkoiIiIgEwcKSiIiIiATBwpKIiIiIBMHCkoiIiIgEwcKSiIiIiATBwpKIiIiIBMHCkoiIiIgEwcKSiIiIiATBwpKIiIiIBMHCkoiIiIgEwcKSiIiIiATBwpKIiIiIBMHCkoiIiIgEwcKSiIiIiATBwpKIiIiIBMHCkoiIiIgEwcKSiIiIiAShJnYAEo6aqgrUVPlZQRlkZueIHaFExIX4ix2hRFj02yR2BMG93e0rdoQS8S6rbL63NNVVxY5AVCCsQoiIiIhIECwsiYiIiEgQLCyJiIiISBAsLImIiIhIECwsiYiIiEgQLCyJiIiISBAsLImIiIhIECwsiYiIiEgQLCyJiIiISBAsLImIiIhIECwsiYiIiEgQLCyJiIiISBAsLImIiIhIECwsiYiIiEgQLCyJiIiISBAsLImIiIhIECwsiYiIiEgQLCyJiIiISBAsLImIiIhIECwsiYiIiEgQLCyJiIiISBAsLImIiIhIECwsqcDWr10DF2d7GOlpoUlDD1yJjBQ7UrFFnDuLHl07wcHWCtrqEoQc2C92pELbtGE9GtarBRsLY9hYGKN180Y4ceyI7PngTT+jQ1tP2FgYw0hHDUlJSeKFLYSlixeieSMPVDAzhJOtJb7p1Q2PHz2Ua/P0aRT69+4ORxsLWJsbYXD/PoiPixMp8adUVCSY0c8dD9b3ReKOIbi3rg+m9Kr1STsXayPsDmiD2F8H4/Xv3oj4sStsTHVlz/u0roxjczog7rfBeLfPF4Y6GqXZjWJR5uNG3eqVUN5I85MlYMIYAEB8XCxGDRsCt0q2cLQyRuumHgg9sE/k1MWjzOP1OWWxT4Di9qtAhWVISEiBl7IqNjYWo0ePhqOjIzQ1NWFjY4NOnTohLCxMsNewt7dHUFCQYPsT0u5dOzF5oj+m/TATFyOvw82tBjp3aIv4+HixoxVLeno6qrvVQNDKNWJHKTKrChUwK3AeTp+PRHjEZTRt1gLf9O6OB/fvAQAy3mWgVeu28J84ReSkhXP+3Bn4Dh+Bk2cuYH/oMWR/yEa3jl5IT08HkDd23Tp6ARIJDh45iWOnziE7Kwt9enSBVCoVOX2e8d1qwNfLFeN+Po+ao3fjh22R8O/mhu87VJW1cbDUR9j8Tnj0Mgltp4ei7rg9WLD7Ot5n58ja6Giq4cSNv7F4z00RelF0yn7cOBJ+Hrce/iVbdu4/DADo1KUHAGD0cB9EPXmErb/vQfiFa2jfqSu+G/IN7ty6KWLqolP28cpPWewToNj9kuTm5uZ+rZGKSsFObEokEuTk5Hy9oZJ5/vw5GjVqBCMjIwQGBqJ69erIzs7GsWPHsGHDBvz555+CvI69vT38/Pzg5+dXqO1SUlJgaGiIuDfJMDAwECTLx5o09IB7nboIWrkaACCVSuHsYIMRI0dj4iTlKlg+R1tdgp1/7EPnLl1L/LUys0v2fWJfwQyB8xZhkLePbN25s6fRyasVnr96DSMjoxJ5XYlEUiL7BYDXCQlwsrXE4RPhaNS4KcJOHkfPLh3wV8wb2e99cnIy7MqXw77Qo2jh2Uqw17bot6lI2+2Z1hbxSe8wYs1Z2brfJ7XCu6wP8Ak6DQDY5u+J7Bwpvl1x+qv7a1K1PI7P7QjL/luRnJFVpEz/eLvbt1jbF4QYx42k9OL9XL5k+pTxOHnsMC5cvw+JRAKnCiZYuHQVevXtL2vj6lAe02bPQ/9BPl/YU+EZ6Zb8WeqyeJwvi30CxOlXSkoKLMoZIjn5y7VGgSpGqVRaoKUsFpUA8P3330MikSAyMhI9evRApUqVULVqVfj7++PSpUsAgOjoaHTp0gV6enowMDBA7969Efefr+SioqLQpUsXWFhYQE9PD3Xr1sXJkydlzzdv3hx//fUXxo0bB4lEUqJ/oAsrKysLN65fg2fLf/9Qq6iowNOzFSIvXRQxGX0sJycHe3bvREZ6Oup51Bc7jqCSU5IBAMbGJgCArMxMSCQSaGpqytpoaWlBRUUFly6cFyXjxy79GYcWblZwtjIEAFS3N0GDKhY4fv0FAEAiAbzq2ODxq2SEzGiHv4IH4OyiLuhUz07M2IIoa8eNrKws7Nn1O/oO8JYdn+vUq4+Qfbvx9m0ipFIp9u/ZhfeZ79GwcVOR0xZeWRsvoGz2CVD8fhXrGsv3798LlUNhJSYm4ujRoxg5ciR0dXU/ed7IyAhSqRRdunRBYmIizpw5gxMnTuDp06fo06ePrF1aWhrat2+PsLAw3LhxA15eXujUqROio6MBAHv37oW1tTUCAwMRExODmJiYz2bKzMxESkqK3FKSXr9+jZycHJibW8itN7ewQGxsbIm+NhXMvbt3UMHMEOZGOhg35nv8uuMPVK7iKnYswUilUgRMHIf6DRrBtWo1AEDdevWhq6uLmdOmICMjA+np6fhhykTk5OQgNvbz75/StGTvTeyOiMKtVb2QsvtbXFraHasP3sWOs1EAAHNDbehra2BC9xo4ceMFOs06jJDLz7Fjcms0rmopcvriKWvHjaOHQpCSnIQ+3wyUrduwZTuys7Ph6lAedub6mDRuJDb/ugsOjs4iJi2asjZeQNnsE6D4/Sp0YZmTk4M5c+agQoUK0NPTw9OnTwEA06dPx6ZNRfu6SJE9efIEubm5qFy58mfbhIWF4c6dO9i+fTvc3d3h4eGBbdu24cyZM7hy5QoAoEaNGvjuu+9QrVo1VKxYEXPmzIGTk5PsulQTExOoqqpCX18flpaWsLT8/B+VBQsWwNDQULbY2NgI22lSOhUrueDcpWsIO3MB3/p+hxHDfPDng/tixxLMeL9ReHDvHjZv2y5bZ2pmhuDfduLI4VBYmRrAxsIYyclJqFGrdoEv3ylpPRs5om9TZ3gvP4UG4/di6MrT8Ovqhv4tKgIAVP535is08i+sOngXt58nYsneWzh8NRq+bauIGZ0+sv2XLfBs1RaW5a1k636cNwspycnYdeAIjoZfxHffj8V33v3x4N5dEZMSiavQR9958+YhODgYP/74IzQ0/r3mo1q1ati4caOg4RRBAS5BxYMHD2BjYyNX4Lm6usLIyAgPHjwAkHfGcsKECahSpQqMjIygp6eHBw8eyM5YFkZAQACSk5Nly4sXLwq9j8IwNTWFqqoq4uPl77aNj4v7YgFMpUdDQwOOTs6oWdsdMwPno1p1N6xfs0rsWIKY4Dcaxw4fwsFjYahgbS33XMtWbXDr/mNERcfi6d/x2LB5G2JevYS9vaNIaeXNH+yBJXtvYXfEU9yLfovfzzzBqpC7mNi9JgDgdep7ZH+Q4sGLJLntHv6dBBtTvdIPLKCydNx4Ef0Xzp0+hW8GDZGte/4sCpt/XoflqzegSTNPVK3uhvFTfkCNWrWxZeM6EdMWTVkar3+UxT4Bit+vQheW27Ztw4YNG9C/f3+oqqrK1teoUUOwm1gUScWKFSGRSIrdtwkTJmDfvn2YP38+zp07h5s3b6J69erIyir8heaampowMDCQW0qShoYGatV2R/ipf++Al0qlCA8PQ736DUr0talopFIpMrMyxY5RLLm5uZjgNxqhIftx8OhJ2Ns7fLZtOVNTGBkZ4czpU0iIj0f7jp1KMennaWuqQSqV/3CaI5VCRSXvTGX2BymuPUlApQqGcm0qWhkiOiGt1HKWhLJ03Nj52zaYmpmjVdv2snXvMt4BACQq8tfDq6iqKsysBIVRlsbrH2WxT4Di90utsBu8fPkSzs6fXj8ilUqRnZ0tSChFYmJigrZt22LNmjUYM2bMJ9dZJiUloUqVKnjx4gVevHghO2t5//59JCUlwdU17zq38+fPw9vbG926dQOQdwbz+fPncvvS0NBQ2Bugxvj5w9dnMNzd66BO3XpYvTIIGenpGDR4yNc3VmBpaWmIevJE9vj5s2e4dfMmjE1MYGtrK2Kygps9YypatfGCtY0t0lJT8ceu3xFx9gz2huRNjRIXG4u4uFg8i8q7ru/+vTvQ09OHjY0tjE1MxIz+ReP9RuGPnb9j++590NPTR9z/rh0yMDSEtrY2AODXbVvg4lIF5czMcOXyRUyeMA4jR/uhYiUXMaPLHL4Sjck9a+LF6zTcj36Lmo6mGNO5OraFPZK1Wb7/Nn4Z74mI+zE4cycGbWpZo31dW7SdHiprY2GkDQsjbTiVz/sQWc3OBKnvsvDidTrepinuB4iycNyQSqXY8ds29O43AGpq//7JdK7kAgdHJ0zyG4WZcxfC2MQER0NDcDY8DL/sVM65LMvCeH2sLPYJUOx+FbqwdHV1xblz52BnJ3/X4h9//IFatT6d+LcsWLNmDRo1aoR69eohMDAQbm5u+PDhA06cOIF169bh/v37qF69Ovr374+goCB8+PAB33//PZo1a4Y6deoAyDvzuXfvXnTq1AkSiQTTp0//5FOtvb09zp49i759+0JTUxOmpqZidDdfvXr3weuEBATOnoG42Fi41aiJA6FHYWFh8fWNFdj1a1fRtlUL2ePJE/0BAAMGDsbPm4NFSlU4CfEJGD50COJiY2BgaIiq1apjb8hhtGjZGgCweeNPWDR/jqx9+9Z5/V3z0yb0HzhYlMwFsWnDegBAhzaecuvXbtiE/gO9AQCPHz3C7BnT8DYxEbZ29pgwaSpGjvEr5aSf5//zBcz8xh0rhjWCmaE2Yt5mYNPxPzF/13VZm5DLzzH6pwhM7F4TS79tiEevktHvx5O48ODfr7mGtq2CH/q6yx6fnJ93RtZ35Wn8Gv649DpUSGXhuHH2dBhe/h2NvgPk3yvq6ur4dfcBzJv1Awb17Y709DQ4ODhhxbpNaNmmnUhpi6csjNfHymKfAMXuV4HmsfyvAwcOYPDgwQgICEBgYCBmz56Nhw8fYtu2bQgNDUXr1q1LKquoYmJiMG/ePISGhiImJgZmZmZwd3fHuHHj0Lx5c0RHR2P06NEICwuDiooKvLy8sGrVKtkgP3/+HD4+Prh06RJMTU0xefJk7N69GzVr1pRNin7p0iV89913ePjwITIzMwt0fSdQOvNYkrBKeh5LsSjSNFlCKuo8loqsNOaxFENJzmMpptKYx5LoSwo6j2WhC0sAOHfuHAIDA3Hr1i2kpaWhdu3amDFjBtq0aVOs0FQ0LCyVDwtL5cLCUnmwsCQqGQUtLAv9VTgANGnSBCdOnChyOCIiIiIqe4pUWALA1atXZVPpuLq6wt3d/StbEBEREVFZVujC8u+//0a/fv1w/vx52f83nJSUhIYNG2LHjh2w/mieOSIiIiL6/6HQ81gOHToU2dnZePDgARITE5GYmIgHDx5AKpVi6NChJZGRiIiIiJRAoc9YnjlzBhcuXICLy7/zxLm4uGDVqlVo0qSJoOGIiIiISHkU+oyljY1NvhOh5+TkwMrKKp8tiIiIiOj/g0IXlosXL8bo0aNx9epV2bqrV69i7NixWLJkiaDhiIiIiEh5FOircGNjY7n56dLT0+Hh4SH7760+fPgANTU1+Pj4oGvXriUSlIiIiIgUW4EKy3/+ZxgiIiIios8pUGE5eLDi/n/CRERERKQYijxBOgC8f/8eWVny/30W/0tBIiIiov+fCn3zTnp6OkaNGgVzc3Po6urC2NhYbiEiIiKi/58KXVhOmjQJp06dwrp166CpqYmNGzdi9uzZsLKywrZt20oiIxEREREpgUJ/FX7w4EFs27YNzZs3x5AhQ9CkSRM4OzvDzs4Ov/32G/r3718SOYmIiIhIwRX6jGViYiIcHR0B5F1PmZiYCABo3Lgxzp49K2w6IiIiIlIahS4sHR0d8ezZMwBA5cqVsWvXLgB5ZzKNjIwEDUdEREREyqPQheWQIUNw69YtAMCUKVOwZs0aaGlpYdy4cZg4caLgAYmIiIhIORT6Gstx48bJ/t2qVSv8+eefuHbtGpydneHm5iZoOCIiIiJSHsWaxxIA7OzsYGdnJ0QWIiIiIlJiBSosV65cWeAdjhkzpshhiP6/0FRXFTsCFcLb3b5iRxCccd1RYkcoEW+vrBY7QonIzc0VO0KJkEgkYkcoEWVxvArapwIVlsuXLy/QziQSCQtLIiIiov+nClRY/nMXOBERERHR5xT6rnAiIiIiovywsCQiIiIiQbCwJCIiIiJBsLAkIiIiIkGwsCQiIiIiQRSpsDx37hwGDBiABg0a4OXLlwCAX375BREREYKGIyIiIiLlUejCcs+ePWjbti20tbVx48YNZGZmAgCSk5Mxf/58wQMSERERkXIodGE5d+5crF+/Hj///DPU1dVl6xs1aoTr168LGo6IiIiIlEehC8uHDx+iadOmn6w3NDREUlKSEJmIiIiISAkVurC0tLTEkydPPlkfEREBR0dHQUIRERERkfIpdGHp6+uLsWPH4vLly5BIJHj16hV+++03TJgwASNGjCiJjERERESkBAr0f4X/15QpUyCVStGyZUtkZGSgadOm0NTUxIQJEzB69OiSyEhERERESqDQhaVEIsG0adMwceJEPHnyBGlpaXB1dYWenl5J5CMiIiIiJVHowvIfGhoacHV1FTILERERESmxQheWLVq0gEQi+ezzp06dKlYgIiIiIlJOhS4sa9asKfc4OzsbN2/exN27dzF48GChchERERGRkil0Ybl8+fJ818+aNQtpaWnFDkREREREyqlI/1d4fgYMGIDNmzcLtTsiIiIiUjKCFZYXL16ElpaWULsjIiIiIiVT6MKye/fucku3bt1Qv359DBkyBN99911JZCQFsX7tGrg428NITwtNGnrgSmSk2JEEwX4pj4hzZ9Gjayc42FpBW12CkAP7xY4kGGUbLz0dTSye0AMPDwci8eIyhAf7w93VVva8rrYGlk/uhSdH5yDx4jJc3zMNQ3s2/uz+9q8egXc3VqNTc7fSiF9syjZeX1O5ogN0NFQ+WfzGjBQ7WrFsWL8OdWu5wdzEAOYmBmjWuAGOHT0idqximxs465OxqlmtitixABShsDQ0NJRbTExM0Lx5cxw+fBgzZ84siYxKzdvbG127di1w++fPn0MikeDmzZsllqkodu/aickT/THth5m4GHkdbm410LlDW8THx4sdrVjYL+WSnp6O6m41ELRyjdhRBKWM47VuxjfwrF8ZPj9sRZ3e83Hy4p84tH40rMwMAQCLxvdA64auGDJtG2p2n4vVv53G8sm90KFZ9U/2Nbp/C+TmlnYPik4Zx+trzl2IxNPoV7Il9MhxAED3Hr1ETlY8FaytMWf+Qly4fA3nL11F8xae6NW9C+7fuyd2tGJzda0qN2YnT58TOxKAQhaWOTk5GDJkCJYtW4YtW7Zgy5Yt2LRpExYuXIg2bdqUVEZBJCQkYMSIEbC1tYWmpiYsLS3Rtm1bnD9/XuxoSmFl0DIM+dYXg7yHoIqrK1atXQ9tHR1sDVbu62rZL+XS1qsdZgXORZeu3cSOIihlGy8tTXV0bVkT04L24/z1KDx98RrzfjqMqBcJ8O3VBABQv4YDfg29jHPXHiM6JhGb957H7UcvUaeqndy+3CpVwNiBnhg+61cxulIkyjZeBWFmZgZLS0vZcuRwKBydnNCkaTOxoxVLh46d4NWuPZwrVkTFSpUwe8486OnpIfLyJbGjFZuqmprcmJmamoodCUAhC0tVVVW0adMGSUlJJRSn5PTo0QM3btzA1q1b8ejRI4SEhKB58+Z48+aN2NEUXlZWFm5cvwbPlq1k61RUVODp2QqRly6KmKx42C9SBMo4XmqqKlBTU8X7rGy59e8zs9GwlhMA4NKtZ+jYrLrsDGbTOhVR0c4cJy89kLXX1lJH8AJv+C3chbg3qaXXgWJQxvEqrKysLOzY/hsGDR7yxXmrlU1OTg527dyB9PR0eNRvIHacYot68hiOdhXg6uKEIYMG4EV0tNiRABThq/Bq1arh6dOnJZGlxCQlJeHcuXNYtGgRWrRoATs7O9SrVw8BAQHo3LkzAGDZsmWoXr06dHV1YWNjg++//15u+qTg4GAYGRnh2LFjqFKlCvT09ODl5YWYmBhZm5ycHPj7+8PIyAjlypXDpEmTkPvR9ztHjx5F48aNZW06duyIqKio0vlBFNHr16+Rk5MDc3MLufXmFhaIjY0VKVXxsV+kCJRxvNIyMnHp1lME+LZDeTNDqKhI0Ld9XXi4OcDS1AAA4L9oNx48jUXU8XlIiVyBkDXfw2/hLpy//u/x7sfxPXDp1jOEnr4jVlcKTRnHq7AOHtiPpKQkDBjkLXYUQdy9cwemRnow1NXEmJHDsfOPfaii5P9zYN16HtiwcQsOHDyCFavW4vnzZ2jl2RSpqeJ/QCt0YTl37lxMmDABoaGhiImJQUpKityiiPT09KCnp4f9+/cjMzMz3zYqKipYuXIl7t27h61bt+LUqVOYNGmSXJuMjAwsWbIEv/zyC86ePYvo6GhMmDBB9vzSpUsRHByMzZs3IyIiAomJidi3b5/cPtLT0+Hv74+rV68iLCwMKioq6NatG6RSaYH7k5mZqRQ/dyIqu3x+2AaJBHh6fB6SLwdhZL9m2HX0KqTSvA/T3/dthnrV7dFj7Ho07L8IU5btQ9CU3mjh4QIA6NCsOprXq4SJi/8QsxuUj63Bm9GmbTtYWVmJHUUQlVxccPnqTZw9fxm+342Ar89gPLh/X+xYxdLWqx269+yF6m5uaN2mLfaFHEJyUhL2/LFL7GiFnyC9ffv2AIDOnTvLnSLPzc2FRCJBTk6OcOkEoqamhuDgYPj6+mL9+vWoXbs2mjVrhr59+8LNLe8ORD8/P1l7e3t7zJ07F8OHD8fatWtl67Ozs7F+/Xo4OeV91TNq1CgEBgbKng8KCkJAQAC6d+8OAFi/fj2OHTsml6VHjx5yjzdv3gwzMzPcv38f1apVK1B/FixYgNmzZxf8B1BMpqamUFVVRXx8nNz6+Lg4WFpalloOobFfpAiUdbye/f0abYaugI6WBgz0tBD7OgW/LByCZy9fQ0tTHbNHd0If/59xNCLvJom7j1/BzcUafgNbIvzyQzSvWwmO1qaIPbtYbr+/LxmK8zei0NZ3hRjd+iplHa+Civ7rL5wKO4nfd+0RO4pgNDQ04OTsDACo7e6Oa1evYM2qFVi97ieRkwnHyMgIzhUr4emTJ2JHKfwZy/DwcNly6tQp2fLPY0XVo0cPvHr1CiEhIfDy8sLp06dRu3ZtBAcHAwBOnjyJli1bokKFCtDX18fAgQPx5s0bZGRkyPaho6MjKyoBoHz58rK7AJOTkxETEwMPDw/Z82pqaqhTp45cjsePH6Nfv35wdHSEgYEB7O3tAQDRhbg2IiAgAMnJybLlxYsXhf1xFIqGhgZq1XZH+Kkw2TqpVIrw8DDUU+LrVNgvUgTKPl4Z77MQ+zoFRvraaNWwCkJP34G6mio01NUg/ehSoJwcKVRU8k5ILNlyHHV7L4BH34WyBQAmLd2DYTMV90YeZR+vr9m2dQvMzM3Rrn0HsaOUGKlU+tlvL5VVWloanj2NgmX58mJHKfwZSwcHB9jY2HxyQW9ubm6JFzjFpaWlhdatW6N169aYPn06hg4dipkzZ6J58+bo2LEjRowYgXnz5sHExAQRERH49ttvkZWVBR0dHQCAurq63P4kEskn11B+TadOnWBnZ4eff/4ZVlZWkEqlqFatGrKysgq8D01NTWhqahbqdYtrjJ8/fH0Gw929DurUrYfVK4OQkZ6OQYOHlGoOobFfyiUtLQ1R//lE/vzZM9y6eRPGJiawtbX9wpaKTRnHq1WDKpBIgEfP4+FkY4b547ri0bM4bAu5iA8fpDh79THm+3XFu/fZiI5JRBN3Z/TvWA+Tl+0FAMS9Sc33hp0XMW/x1yvFvqlSGcerIKRSKX7ZFowBAwZBTa3Q5YFCmj4tAG292sHGxhapqanYuWM7zp45jYOHj319YwUWMHkC2nfoBFtbO8TEvMLcwFlQVVVFrz79xI5WtMIyJiYG5ubmcusTExPh4OCgkF+Ff46rqyv279+Pa9euQSqVYunSpVBRyTuJu2tX4a5TMDQ0RPny5XH58mU0bdoUAPDhwwdcu3YNtWvXBgC8efMGDx8+xM8//4wmTfKm5IiIiBCwRyWnV+8+eJ2QgMDZMxAXGwu3GjVxIPQoLCwsvr6xAmO/lMv1a1fRtlUL2ePJE/0BAAMGDsbPm4NFSlV8yjhehnpaCBzdGRUsjJCYnIEDYTcxc81BfPiQd734oCmbETi6C4LnD4axgQ6iYxIxa00oft6tHMe8L1HG8SqIU2En8SI6GoO8fcSOIpiE+Hh8O2QQYmNiYGhoiGrV3XDw8DG0bNVa7GjF8vLvlxg88BskvnkDUzMzNGzYGKfPXYSZmZnY0SDJLeQpNxUVFcTFxX0S/q+//oKrqyvS09MFDSiEN2/eoFevXvDx8YGbmxv09fVx9epVjB49Gh06dMCYMWNQs2ZNBAUFoVOnTjh//jwCAgLw8uVLvH37FkZGRggODoafn5/cVEv79+9Ht27dZGctFy1ahB9//BGbNm1C5cqVsWzZMuzYsQOenp7Yv38/pFIpzM3N0a5dO8ycORPR0dGYMmUKrly5gn379qFr1654/vw5HBwccOPGDdSsWbNA/UtJSYGhoSHi3iTDwMCgBH6CRFTWGNcdJXaEEvH2ymqxI5SIwn47pizK0nRG/1UWxyslJQWWpkZITv5yrVHgM5b+/nlnBiQSCaZPny77ehjIm2bn8uXLBS6ESpuenh48PDywfPlyREVFITs7GzY2NvD19cXUqVOhra2NZcuWYdGiRQgICEDTpk2xYMECDBo0qFCvM378eMTExGDw4MFQUVGBj48PunXrhuTkZAB5RfmOHTswZswYVKtWDS4uLli5ciWaN29eAr0mIiIiKl0FPmPZokXe109nzpxBgwYNoKGhIXtOQ0MD9vb2mDBhAipWrFgySemzeMaSiAqLZyyVS1k8AwbwjKUyEfyMZXh4OABgyJAhWLFiBQsYIiIiIpJT6Jt3tmzZUhI5iIiIiEjJFXoeSyIiIiKi/LCwJCIiIiJBsLAkIiIiIkGwsCQiIiIiQbCwJCIiIiJBsLAkIiIiIkGwsCQiIiIiQbCwJCIiIiJBsLAkIiIiIkGwsCQiIiIiQbCwJCIiIiJBsLAkIiIiIkGwsCQiIiIiQbCwJCIiIiJBsLAkIiIiIkGwsCQiIiIiQbCwJCIiIiJBqIkdgITzMjEDydlla0htyumIHaFEpGd+EDtCiVBXLZufVcvieL29slrsCCWi4fxTYkcoERemeoodoUR8yJGKHaFEqJXBY6FEIilQu7LXcyIiIiISBQtLIiIiIhIEC0siIiIiEgQLSyIiIiISBAtLIiIiIhIEC0siIiIiEgQLSyIiIiISBAtLIiIiIhIEC0siIiIiEgQLSyIiIiISBAtLIiIiIhIEC0siIiIiEgQLSyIiIiISBAtLIiIiIhIEC0siIiIiEgQLSyIiIiISBAtLIiIiIhIEC0siIiIiEgQLSyIiIiISBAtLIiIiIhIEC0siIiIiEgQLS8KVixH4bmBPNK7hhEqWujhx5OBn286YNAaVLHURvGG13Prhg3qhmbsLqtmZoJGbIyaM+hZxsTElHV0Q69eugYuzPYz0tNCkoQeuREaKHalQFs0LhKmeutxSv1Y1AMDbxERMGT8WHrWqwtpUHzUqOyJggh9SkpNFTv11SxcvRPNGHqhgZggnW0t806sbHj96KNfm6dMo9O/dHY42FrA2N8Lg/n0QHxcnUuKCycnJwY9zZ8HDrRIcLQ3RoGZlLP9xPnJzc/NtP3ncSFgZaeLntStLOakwlO39ZaavgbldXXFqQhNcCGiGnd/VQ5Xy+rLnr8/wzHcZ1MBW1mZ5n+o4NLYhLk5thmPjGmFOV1eY6mmI0Z1CU7bx+ljEubPo1b0zKjpYQ19LFQdD9ss9Hx8Xh++GDkFFB2uYG+uhW6d2ePLksThhi0lRx4qFpQAkEgn279//2edPnz4NiUSCpKSkUstUGBkZ6ahctTpmLFj+xXbHD4fg5rVImFuW/+Q5j0ZNsWLDLzgWcROrNm3Hi+fPMGZo/5KKLJjdu3Zi8kR/TPthJi5GXoebWw107tAW8fHxYkcrlMpVquJe1AvZcujEaQBAbMwrxMbEYPa8RTgXeROr1m9C2MnjGPv9MHEDF8D5c2fgO3wETp65gP2hx5D9IRvdOnohPT0dAJCeno5uHb0AiQQHj5zEsVPnkJ2VhT49ukAqlYqc/vPWBC3B1s0bMG9xEM5cvoVps+dj7cql2PTTmk/aHjl4ANeuRMKyvJUISYtP2d5f+lpq2DLEHR+kuRi9/SZ6rruM5SeeIPX9B1mb1ksj5JZZBx5AmpuLsAf/9unq8yRM+eMuuq+5jIm778DaWBuLe1UXo0uFomzjlZ+MjHRUr14DS4NWffJcbm4u+vbujufPnmHH7n2IuHwNNrZ26Nyujey4oiwUeawkuZ/7mEwyCQkJmDFjBg4dOoS4uDgYGxujRo0amDFjBho1agSJRIJ9+/aha9eu+W6flZWFxMREWFhYQCKRfPZ1vL29kZSU9MUiNT8pKSkwNDTE9ccx0NM3KNS2H6tkqYs1W3agdbtOcutjY16hV/tm2Pz7AQwb0AODh42E97BRn91P2LFD+N67D+5Gv4W6unqR89iU0ynytgXRpKEH3OvURdDKvDOwUqkUzg42GDFyNCZOmlJir5ue+eHrjQpo0bxAHAk9gNMXrxWo/YG9f2DE0MGIjk+GmpqaYDkAQF215D6rvk5IgJOtJQ6fCEejxk0RdvI4enbpgL9i3sDAIO/3Pjk5GXbly2Ff6FG08Gwl2GsLOV6D+nSFqZkFlq3+SbZu6MA+0NLWxuoNwbJ1Ma9eomOrJti+JxQDe3eF74hR8P1+jGA5jHVL/gyaGO+vhvNPFXnb0S2dUNPGEN8GXy/wNkt7V4eupiqG/3Lzs22aVjLFsj7VUX/eaXyQFu1P7oWpnkXarjDEGK8POSX3IVBfSxXbd+1Bp85dAQCPHz9C7epVEHn9Nqq4VgWQ10cnOyvMnD0X3j5DBXtttRI8FgLijFVKSgosyhkiOTlZdszND89YFkCPHj1w48YNbN26FY8ePUJISAiaN2+ON2/eFGh7DQ0NWFpafraozMnJUegzLFKpFJNGfYuh3/uhYmXXr7ZPepuIkD07Uatu/WIVlSUtKysLN65fg2fLfwsQFRUVeHq2QuSliyImK7ynUU9Q1dkW7tUq4Tufgfj7RfRn26akJENf30DworKkJafkfX1vbGwCAMjKzIREIoGmpqasjZaWFlRUVHDpwnlRMhZEnXoNEHEmHFFPHgEA7t25jchLF+DZqq2sjVQqxZjvfDBi9Di4VPn6e04RKeP7q1klU9x/lYJFPavh5PjG2O5bF91qff5ssYmuOhpXLIf9Nz5/2Y+BlhraV7fArRfJRS4qS4MyjldhZWVmAgA0NbVk61RUVKCpoYmLCnzM+JiijxULy69ISkrCuXPnsGjRIrRo0QJ2dnaoV68eAgIC0LlzZ1m7169fo1u3btDR0UHFihUREhIie+7jr8KDg4NhZGSEkJAQuLq6QlNTEz4+Pti6dSsOHDgAiUQCiUSC06dP55spMzMTKSkpcktJ2rB6KVTV1DBo6PdfbLd4zg+o4WCGelVsEPPyBdYF7yzRXMX1+vVr5OTkwNzcQm69uYUFYmNjRUpVeO5162HV+k3YtT8Ui4NWI/qv5+jYpgVSU1M/afvm9WssXTQfg4YI98m8NEilUgRMHIf6DRrBtWre9aN169WHrq4uZk6bgoyMDKSnp+OHKRORk5ODWAW+vnfUuIno0qMXmtZ1g62pLto0rQffEaPRvXc/WZs1QUugqqaKb4d//lsBRaeM768KxlroWacCXiRmYORvN/HHtZeY6FURHd0s823fqUZ5ZGTl4NSDhE+eG9PSCeenNMPpSU1haagF/523Szp+sSjjeBVWJZfKsLGxxawZU/H27VtkZWVh2ZIf8fLl30pzTwCg+GPFwvIr9PT0oKenh/379yPzf5928jN79mz07t0bt2/fRvv27dG/f38kJiZ+tn1GRgYWLVqEjRs34t69e1i5ciV69+4NLy8vxMTEICYmBg0bNsx32wULFsDQ0FC22NjYFLufn3P31g1s+3ktFq7Y8MWv8QHg2+/9sP/kBWzZGQIVVVVMGu372RsSSDit2nihS/eeqFrNDZ6t2mDHnoNITk7Cgb275dqlpqSgX8/OcKlcBZOmzRApbdGM9xuFB/fuYfO27bJ1pmZmCP5tJ44cDoWVqQFsLIyRnJyEGrVqQ0VFcQ9tIfv+wN7dO7Bm4zYcO3MZK9ZtwvpVy7Fr+y8AgNs3r2Pj+tUIWrvxq+85EpaKRII/Y9Kw+tRTPIxNw97rr7Dv+iv0rFMh3/ada5bHkTuxyMrn69xtF6LRb0MkRvx6AznSXAR2Vc4zz2WJuro6ftv5B548fgzb8qYwN9bDuTPhaNPWS6GPGcqGP8mvUFNTQ3BwMLZu3QojIyM0atQIU6dOxe3b8p8+vb290a9fPzg7O2P+/PlIS0tD5Bfu0MrOzsbatWvRsGFDuLi4wMDAANra2tDU1ISlpSUsLS2hoZH/NVABAQFITk6WLS9evBC0z/919fJ5vHmdgObuLqhSwQBVKhjg5d/RWDgrAC3qVJFra1LOFA5OFdGoWUsErd+KM2HHcPOaYtyllh9TU1OoqqoiPl7+LuL4uDhYWuZ/hkIZGBoZwcm5Ip49jZKtS01NRe9uHaCnp4+tv/+h0JcofGyC32gcO3wIB4+FoYK1tdxzLVu1wa37jxEVHYunf8djw+ZtiHn1Evb2jiKl/bo5MwIwym8CuvbojSpVq6Fn3/7w/X4MVi3/EQBw+UIEXifEo241Z9iU04FNOR38/eIvzP5hMupVryRy+oJTxvfX69QsPE2Qv4nj2esMWBpofdK2lq0hHEx1se8zX4MnvctGdOI7XH76FgF77qFJRVO4WRfvGviSpIzjVRS1arvjQuR1/B2XiMfPX2LfwSNITEyEvYPiHjM+puhjxcKyAHr06IFXr14hJCQEXl5eOH36NGrXro3g4GBZGzc3N9m/dXV1YWBg8MW7szQ0NOS2KQxNTU0YGBjILSWlS89+OHjqMg6cvChbzC3L49vv/bBpx4HPbvfPNaNZXzjLKzYNDQ3Uqu2O8FNhsnVSqRTh4WGoV7+BiMmKJy0tDc+fPYWFRd4BJjUlBb26tIO6ugZ+3bUPWlqf/pFURLm5uZjgNxqhIftx8OhJ2Ns7fLZtOVNTGBkZ4czpU0iIj0f7jp0+21Zs7zMyPjk7oqqqitz/vWd69O2PsPPXcOLcFdliWd4KI8b4Y/vez08FpmiU8f1180US7E3lbxi0K6eNmOT3n7TtUtMK91+l4HFc2lf3q/K/E88leXNbcSnjeBWHoaEhzMzM8OTJY1y/dhUdOnb++kYKQtHHSrmu3heRlpYWWrdujdatW2P69OkYOnQoZs6cCW9vbwD45AyQRCL54g052traCvM1V3p6Gv569u/Zrb+jn+P+3VswMjKBlbUNjE3KybVXV1OHmbkFHJ3zzp7cun4Ft29cg7tHAxgaGiP6r6dYsWgObO0dUauOR6n2pbDG+PnD12cw3N3roE7deli9MggZ6ekYNHiI2NEKbMbUSWjbriNsbG0RG/MKi+YFQlVFFd179UVqSgp6dmmHdxkZWLdxK1JTU5CamndNrqmpGVRVVUVO/3nj/Ubhj52/Y/vufdDT00fc/64dMjA0hLa2NgDg121b4OJSBeXMzHDl8kVMnjAOI0f7oWIlFzGjf1Frrw5YuXQRKljbwKWyK+7evoWf1qxA3wGDAQAmJuVg8tF7Tk1NHebmFnCuqLj9yo+yvb9+u/wCW4a4w6exHU7ci0fVCgboXrsC5ob+KddOV0MVrV3NsezEp/MfVqtggKpW+rgRnYzU9x9gbayNES0c8CIxA7f/Vuz5Y5VtvPKTlpaGp1FPZI//ev4ct2/dhLGxCWxsbbFvz26YmprB2sYW9+7dweTx49Cxcxe0bN1GxNSFp8hjxcKyiFxdXQs9LdDXaGhoICcnR9B9FsTdm9cxsEc72eMFM/OmKujWuz8Wrdzw1e21tLVx4vABrFoyDxkZ6TA3t0STFq0RtGEyNP5zx64i6tW7D14nJCBw9gzExcbCrUZNHAg9CgsLi69vrCBevXyJYUMG4G3iG5QzNYNHg0Y4Gh4BUzMzRJw9g2tX8i5HqOtWWW676/cew9bOXoTEBbNpw3oAQIc28tOsrN2wCf0HegMAHj96hNkzpuFtYiJs7ewxYdJUjBzjV8pJC2fuj8vx47xZCBg/Fm9ex8PCsjwGDhmKcZOmiR1NcMr2/rr/KhUTdt3BKE8n+Da1x6u377Hk2GMcuSv/lWPbahaABDh299PJ+N9n58Czsjm+a+YIbQ0VvE7NwoWoN5h87jmycxT7mnNlG6/83Lh2Fe3btpQ9Dpg0HgDwzYBB+GnjFsTGxiJg0gTEx8fB0rI8+vUfiMlTfxArbpEp8lhxHsuvePPmDXr16gUfHx+4ublBX18fV69exejRo9GhQwds2rQp33ksjYyMEBQUBG9vb5w+fRotWrTA27dvYWRkhODgYPj5+X0yYfr8+fPx008/4fjx4yhXrhwMDQ0LdC2ckPNYKpqSnsdSLELOi6hIFPmrvuIoi+NVGvNYiqE481gqstKYx1IMJTmPpZhKeh5LMRR0HkuesfwKPT09eHh4YPny5YiKikJ2djZsbGzg6+uLqVOnCvpavr6+OH36NOrUqYO0tDSEh4ejefPmgr4GERERUUnhGcsygGcslU9ZPAMG8IylMuEZS+XCM5bK5f/zGcuy13MiIiIiEgULSyIiIiISBAtLIiIiIhIEC0siIiIiEgQLSyIiIiISBAtLIiIiIhIEC0siIiIiEgQLSyIiIiISBAtLIiIiIhIEC0siIiIiEgQLSyIiIiISBAtLIiIiIhIEC0siIiIiEgQLSyIiIiISBAtLIiIiIhIEC0siIiIiEgQLSyIiIiISBAtLIiIiIhIEC0siIiIiEoSa2AFIOBVMdGBgoCN2DCoAXU2+9ZSJhpqG2BEEl5mdI3aEEnFhqqfYEUqEcbNpYkcoEW/PzBM7QonI/iAVO4LgCtonnrEkIiIiIkGwsCQiIiIiQbCwJCIiIiJBsLAkIiIiIkGwsCQiIiIiQbCwJCIiIiJBsLAkIiIiIkGwsCQiIiIiQbCwJCIiIiJBsLAkIiIiIkGwsCQiIiIiQbCwJCIiIiJBsLAkIiIiIkGwsCQiIiIiQbCwJCIiIiJBsLAkIiIiIkGwsCQiIiIiQbCwJCIiIiJBsLAkIiIiIkGwsCQiIiIiQbCwJCIiIiJBsLCkAlu/dg1cnO1hpKeFJg09cCUyUuxIgmC/lAv7pZg2bViPhvVqwcbCGDYWxmjdvBFOHDvySbvc3Fz07NIBRjpqCA05IEJSYSjbeOnpaGDx2PZ4uGcCEk/NQvj6YXCvXCHftisndsG78/MwqndD2TpbSyOsm9IND3aPR+KpWbi3yx8/fNsS6mqqpdWFIlO2sfrY0sUL0ayRB6zMDOFoa4l+vbrh8aOH+bbNzc1F9y7tYaCtitCQ/aUb9H9YWArk+fPnkEgkuHnzpthRSsTuXTsxeaI/pv0wExcjr8PNrQY6d2iL+Ph4saMVC/ulXNgvxWVVoQJmBc7D6fORCI+4jKbNWuCb3t3x4P49uXZrV6+ARCIRKaUwlHG81k3pBs+6zvAJ/AN1Bq7EycgnOLTCB1amBnLtOjd1Rb2qNniVkCK33sXODCoqEoxafAC1B6zApJWHMbRrPQR+17o0u1FoyjhWH4s4dwbDho9A2JkLOBB6DNkfstG1oxfS09M/abtmlfjvL0lubm6uqAkEkJCQgBkzZuDQoUOIi4uDsbExatSogRkzZqBRo0alkuH58+dwcHDAjRs3ULNmzVJ5zX+kpKTA0NAQcW+SYWBg8PUNiqBJQw+416mLoJWrAQBSqRTODjYYMXI0Jk6aUiKvWRrYL+XCfgknMzunRPb7X/YVzBA4bxEGefsAAG7fuom+PbogPOIyXByt8euOPejYuYugr6mpXvJn0MQYL+Nm04q8rZaGGhJOzECvKb/h6MV/z3Sd3/Q9jl96hNk/nwQAWJka4OzPw9HJPxj7Fg/C6l0XsHrXhc/ud9w3jeHb1QOuvZcWOdvbM/OKvG1BiHXMyP4gLbF9v05IgKOtJY6cCEejxk1l62/fuone3TvjzPlIVHSogO0796Bj566CvW5KSgqsLYyRnPzlWqNMnLHs0aMHbty4ga1bt+LRo0cICQlB8+bN8ebNG7GjFUt2drbYEQAAWVlZuHH9GjxbtpKtU1FRgadnK0ReuihisuJhv5QL+6U8cnJysGf3TmSkp6OeR30AQEZGBnyHDMTi5atgYWkpcsKiU8bxUlNTgZqaKt5nyf9NeZ+ZjYZudgAAiUSCTTN6Yvn2c3jwrGBn8wx0tZCY+k7wvEJRxrEqiOSUZACAsbGJbF1GRga+9R6ApUHiv7+UvrBMSkrCuXPnsGjRIrRo0QJ2dnaoV68eAgIC0LlzZwB5b5iNGzeiW7du0NHRQcWKFRESEiK3n7t376Jdu3bQ09ODhYUFBg4ciNevX8ueP3r0KBo3bgwjIyOUK1cOHTt2RFRU1Gdz5eTkwMfHB5UrV0Z0dDQA4MCBA6hduza0tLTg6OiI2bNn48OHD7JtJBIJ1q1bh86dO0NXVxfz5uX/SS4zMxMpKSlyS0l6/fo1cnJyYG5uIbfe3MICsbGxJfraJYn9Ui7sl+K7d/cOKpgZwtxIB+PGfI9fd/yBylVcAQBTJ41HPY8G6NCps8gpi0cZxystIwuX7vyFAO8WKG+qDxUVCfq2qQGParawNNUHAIwf0AQfcqRYs7tgBZdjBROM6NkAm/Yr7vWKyjhWXyOVSjFl4jjUb9AIrlWrydYHTPKHR/0G6NBJ2G8AikLpC0s9PT3o6elh//79yMzM/Gy72bNno3fv3rh9+zbat2+P/v37IzExEUBecerp6YlatWrh6tWrOHr0KOLi4tC7d2/Z9unp6fD398fVq1cRFhYGFRUVdOvWDVLpp6e7MzMz0atXL9y8eRPnzp2Dra0tzp07h0GDBmHs2LG4f/8+fvrpJwQHB39SPM6aNQvdunXDnTt34OPjk29fFixYAENDQ9liY2NTlB8dEZGgKlZywblL1xB25gK+9f0OI4b54M8H93E49CDOngnHgsXLxI74/5bPnD8gkUjw9MAUJIfPxsheDbHr5G1Ipbmo5WKFkb0aYti8PQXal5WpAUKWeWNv+F1sOXi1hJPTf433G4UH9+5hy7btsnWHQ0Nw5nQ4Fi5eLmKyf6mJHaC41NTUEBwcDF9fX6xfvx61a9dGs2bN0LdvX7i5ucnaeXt7o1+/fgCA+fPnY+XKlYiMjISXlxdWr16NWrVqYf78+bL2mzdvho2NDR49eoRKlSqhR48ecq+7efNmmJmZ4f79+6hW7d9PDWlpaejQoQMyMzMRHh4OQ0NDAHmF7ZQpUzB48GAAgKOjI+bMmYNJkyZh5syZsu2/+eYbDBky5It9DggIgL+/v+xxSkpKiRaXpqamUFVVRXx8nNz6+Lg4WCrxV1rsl3JhvxSfhoYGHJ2cAQA1a7vj+rWrWL9mFbS0tfHsaRTsypeTaz/om15o0KgxDh07JUbcIlHW8Xr2MhFtRm2EjpY6DHS1EPsmFb8E9sGzV2/RqIY9zI118WjPRFl7NTVVLBzVDqN6N0Tlnktk68ub6uPoqm9x6U40Ri7aL0JPCk5Zx+pzxvuNxtHDh3Dk5GlUsLaWrT9zOhzPnkbBxtJErv2Afr3QsFETHD5euu8vpT9jCeRdY/nq1SuEhITAy8sLp0+fRu3atREcHCxr898iU1dXFwYGBrK7wm7duoXw8HDZ2U89PT1UrlwZAGRfdz9+/Bj9+vWDo6MjDAwMYG9vDwCyr7n/0a9fP6Snp+P48eOyovKf1wgMDJR7DV9fX8TExCAjI0PWrk6dOl/tr6amJgwMDOSWkqShoYFatd0RfipMtk4qlSI8PAz16jco0dcuSeyXcmG/lI9UKkVmVibGjZ+E85E3cO7SNdkCAPN/XIo1P20SOWXhKPt4ZbzPRuybVBjpa6FVvYoIPfcA24/eQN1Bq+DhvVq2vEpIwfLt59DJP1i2rZWpAY6tGoobD19i2Pw9UPR7f5V9rP6Rm5uL8X6jERqyHwePnoS9vYPc8/4TJuPilZs4f/m6bAGABT8uw9oNpf/+Uvozlv/Q0tJC69at0bp1a0yfPh1Dhw7FzJkz4e3tDQBQV1eXay+RSGRfY6elpaFTp05YtGjRJ/stX748AKBTp06ws7PDzz//DCsrK0ilUlSrVg1ZWVly7du3b49ff/0VFy9ehKenp2x9WloaZs+eje7du+eb/R+6urpF+wGUsDF+/vD1GQx39zqoU7ceVq8MQkZ6OgYN/vLZVUXHfikX9ktxzZ4xFa3aeMHaxhZpqan4Y9fviDh7BntDDsPC0jLfGwqsrW0/+SOpDJRxvFrVc4ZEIsGj6NdwsjbB/JHt8Cg6AdsOXcOHHCkSU+Rvwsn+kIO4xDQ8js6718DK1ADHVn+L6NgkBKw+CjOjf/9WxSWmlWpfCkMZx+pj/n6j8MfO3/H77n3Q19NH3P+uDzUwNIS2tvZn3182NjaivL/KTGH5MVdXV+zfv79AbWvXro09e/bA3t4eamqf/kjevHmDhw8f4ueff0aTJk0AABEREfnua8SIEahWrRo6d+6MQ4cOoVmzZrLXePjwIZydnYvWIZH16t0HrxMSEDh7BuJiY+FWoyYOhB6FhYXF1zdWYOyXcmG/FFdCfAKGDx2CuNgYGBgaomq16tgbchgtWir2PIdFoYzjZainhcDhbVDBzBCJKe9w4Mw9zPzpOD7kFGxaHM96TnC2MYWzjSmiDkyWe067UdGnQippyjhWH9u0YT0AoH0bT7n16zZsQv+B3iIk+jKln8fyzZs36NWrF3x8fODm5gZ9fX1cvXoVo0ePRocOHbBp0yZIJBLs27cPXbt2lW1nZGSEoKAgeHt749WrV6hZsyaaNWuGSZMmwcTEBE+ePMGOHTuwceNGSCQSmJubo127dpg5cyaio6MxZcoUXLlyRbbfj+exDAoKwvTp03HkyBE0btwYx44dQ8eOHfHDDz+gZ8+eUFFRwa1bt3D37l3MnTsXAPLNWRClMY8lEZUtpTGPpRhKYx5LMRRnHktFVtLzWIqlJOexFEtB57FU+jOWenp68PDwwPLlyxEVFYXs7GzY2NjA19cXU6dOLdA+rKyscP78eUyePBlt2rRBZmYm7Ozs4OXlBRUVFUgkEuzYsQNjxoxBtWrV4OLigpUrV6J58+af3aefnx+kUinat2+Po0ePom3btggNDUVgYCAWLVoEdXV1VK5cGUOHDhXoJ0FEREQkLqU/Y0k8Y0lEhcczlsqFZyyVy//nM5Zl4q5wIiIiIhIfC0siIiIiEgQLSyIiIiISBAtLIiIiIhIEC0siIiIiEgQLSyIiIiISBAtLIiIiIhIEC0siIiIiEgQLSyIiIiISBAtLIiIiIhIEC0siIiIiEgQLSyIiIiISBAtLIiIiIhIEC0siIiIiEgQLSyIiIiISBAtLIiIiIhIEC0siIiIiEgQLSyIiIiISBAtLIiIiIhKEmtgBSDi5ubnIzc0VO4agJBKJ2BGoEKTSsvX794+y+GuooVY2zyuUtWPgP96emSd2hBJh3MBf7Agl4u3FZWJHEJx6AY8ZZfPIQkRERESljoUlEREREQmChSURERERCYKFJREREREJgoUlEREREQmChSURERERCYKFJREREREJgoUlEREREQmChSURERERCYKFJREREREJgoUlEREREQmChSURERERCYKFJREREREJgoUlEREREQmChSURERERCYKFJREREREJgoUlEREREQmChSURERERCYKFJREREREJgoUlEREREQmChSURERERCYKFJRXakh8XQkdDBRPH+4kdpdgizp1Fj66d4GBrBW11CUIO7Bc7kmDWr10DF2d7GOlpoUlDD1yJjBQ7UrHk5OQgcNZ0uFZyRDlDHVSr7IyF8+cgNzdX7GjFMjdwFnQ0VOSWmtWqiB2r2MpqvwDg5cuX8Bk8ENaWpjAx0EHdWm64du2q2LGKZcP6dahbyw3mJgYwNzFAs8YNcOzoEbFjfZGejiYW+3fFw5AfkHhuEcI3jYa7q41cGxd7c+xe6oPY8Hl4fXYBIrb6wcbCSPa8RTl9bJr9DZ4dnYXXZxfgwi/+6NrCrZR7UjSKeoxXEzsAKZerV69g08YNqF5dOd54X5Oeno7qbjUwyNsHfXt1FzuOYHbv2onJE/2xas161K3ngdUrg9C5Q1vcuvcQ5ubmYscrkmVLFmHjhvXYsDEYVVyr4vr1qxju6wMDA0N8P2qM2PGKxdW1KkKPnpA9VlMrG4fmstivt2/fomXzxmjarAX2HTwMM1MzPHnyGMZGxmJHK5YK1taYM38hnJ0rIjc3F7/+shW9unfBpSs34Fq1qtjx8rXuh95wdSoPn5nbEZOQgn7t3HFozXDU7v0jXiUkw6FCOYT9PBpbQy5j7k/HkJL+Hq5Olnif9UG2j42zvoGRvjZ6+W/G6+Q09GlbG78uGIRGg5bj1qOXIvbuyxT5GM8zlkXk7e0NiUQiW8qVKwcvLy/cvn1b7GglJi0tDT6DBmDNug0wMlbug+g/2nq1w6zAuejStZvYUQS1MmgZhnzri0HeQ1DF1RWr1q6Hto4OtgZvFjtakV26eBEdOnWGV/sOsLO3R7fuPdGyVRtcvXpF7GjFpqqmBktLS9liamoqdiRBlMV+LVu8CNbWNtiwcTPq1q0HewcHtGrdBo5OTmJHK5YOHTvBq117OFesiIqVKmH2nHnQ09ND5OVLYkfLl5amOrq2cMO0lQdx/sZTPP37Neb9fAxRL17Dt0dDAMDs79vj2IUHmLYqFLcevcSzl29w6Ow9JLxNk+2nvps91u48h6v3o/H8ZSIWbT6JpNR3qFXFWqyuFYgiH+NZWBaDl5cXYmJiEBMTg7CwMKipqaFjx45ixyox48aMglf79vBs2UrsKPQFWVlZuHH9mtw4qaiowNOzFSIvXRQxWfHUb9AAp8NP4fGjRwCA27dv4cKFCLRp6yVysuKLevIYjnYV4OrihCGDBuBFdLTYkQRRFvt1KPQgaru7o3/f3rCrYIH6dWtj86afxY4lqJycHOzauQPp6enwqN9A7Dj5UlNVgZqaqtzZRwB4n5mNhjUdIJFI4NWoCh5HJyBk5TD8dWw2zm4Zi07Nqsm1v3T7+f+1d99hTWRfH8C/Q0cpogiCgjSliIII9g4KirooYm9YsCtWRFHBXl7X3hZde8Gu6+rasRcsYENRxIYFKwpKS877B7/MErGuYBI9n+fh0cxMknMzycyZO7egdSNXGBkUgSAICGjkCh1tDRy7kPgji/NNlP0Yz4nld9DW1havxF1dXTFq1Cg8ePAAz549AwCEhISgfPnyKFKkCGxsbDB27FhkZ2fLvcakSZNgYmICfX199OzZE6NGjYKrq+tn3zczMxNv3ryR+ytsm6M2IvbSRUyYNLXQ34t9n+fPn0MikcDExFRuuYmpKZ48eaKgqL7fsBGj0DqgLSpXcoRhUS3UrOqG/gMHo137jooO7bt4VK2GP5atwM6/9mLu/EW4ezcJXg3r4u3bt4oO7bv8rOVKSrqDyKVLYGtnh527/0Gv3n0wfMhgrF29StGhfberV67AuJgeDItqY1D/Pojash2OTk6KDuuj0t5l4szlJIT2aAQzYwOoqQlo16QKqlW0QiljA5gU14N+UR0M79oQB07fQPOBS7Er+go2zuiG2m7/1i53Cl0FTQ11PDo0CamnZmD+6AC0HbECdx4+V2DpPk/Zj/Gq3+BFSaSlpWHt2rWws7NDiRIlAAD6+vpYuXIlzM3NceXKFfTq1Qv6+voYOXIkAGDdunWYPHkyFi1ahFq1amHjxo2YNWsWrK2tP/teU6dORURERKGXSebhgwcYMSwYf+3ZDx0dnR/2vozltXXLJkRtXI8Vq9fB0akCLsfFImT4EJiZmaNT566KDu8/8/ZpIv6/YqVK8KhaDQ52Vti6ZRO6BfZQYGTf52ctl1QqhVsVd0yYNAUA4Fq5Mq5fu4plkUvRqYvqfg8BoLy9Pc6ej0Vqaiq2b9uCXt27Yv+ho0qbXHYftx5Lx7XDnb3hyMmRIPZmMjbtv4TKDmWgJggAgN1Hr2H+hmMAgMsJj1CtkhV6taqBExdzayTH92mCYvq6aNJvMV68Tkfzes5YO7UrvHotwLXExwormyrjxPI77N69G3p6egByO4GYmZlh9+7dUFPLrQgOCwsTt7WyssLw4cOxceNGMbGcP38+evTogcDAQADAuHHjsH//fqSlpeFzQkNDMXToUPHxmzdvYGFh8ZlnfJ+LFy8gJSUFNatVEZdJJBKcOH4MSxYtxOu0DKirqxfa+7NvY2xsDHV1daSkPJVbnvL0KUqVKqWgqL7fmNCRGDY8BAFt2gEAnJ0r4sH9e5g1Y5pKJ5YfKlasGOzKlced27cVHUqB+lnKVcrMDA6O8r3b7R0csWP7NgVFVHC0tLRga2cHAHCrUgUXzsdg4fy5WLB4qYIj+7ik5Bdo3HshiuhowaCoNp68eIs1UzojKfkFnr9OR3aOBPFJ8jV4N5NSUNM1t/LGunQJ9G1bB25tpyP+Tu7x8sqtR6hV2Qa9A2ph0LQtP7xMX0PZj/F8K/w7NGjQALGxsYiNjcW5c+fg7e2NJk2a4N69ewCAqKgo1KpVC6VKlYKenh7CwsJwP08bo5s3b6Jq1apyr/nh44/R1taGgYGB3F9hatDQEzEXL+NMzCXxz62KO9q174gzMZc4qVQyWlpaqOxWBUcOHxKXSaVSHDlyCFWVtL3U13j/7p140Sajpq4OqVSqoIgKR1paGpLuJKKUmZmiQylQP0u5atSoJbbzlbl9KwGWlmUVFFHhkUqlyMzMVHQYX/QuIwtPXrxFMX1deFV3wO5jV5GdI8GF6/dRvqx8D+lyliVx//ErAEARHS0AgFQqP2SZRCKFmprwY4L/D5T9GM81lt+haNGisPvf1R0ALFu2DIaGhoiMjISvry86duyIiIgIeHt7w9DQULzVrWr09fVRwVm+wXPRokVRvETxfMtVTVpaGhLz1KDcTUpCXGwsjIoXh6WlpQIj+z6DgoeiV/euqFLFHe4eVbFg3hy8S09Hl66Big7tP2vi2xwzpk+BhYUlHJ0qIC7uEhbMnY3OKlwmAAgNGY6mvs1haVkWjx8/wqQJ4VBXV0dA2/aKDu27/KzlGjA4GA3r1sKMaVPg37oNzsecw5/LIrFgkXLW6n2tsWNC4e3TBBYWlnj79i2iNq7HsaPR+GvPPkWH9kle1e0hCAIS7qXAtowxpgxujoS7KVi9K3c8x9lrorFmSmecuHQHR8/fRuMaDmhaxwnefRYBAG7efYrb959hQWgAQuf+hRep6WhR3xme1cqj1ZDlCizZlynzMZ4TywIkCALU1NTw/v17nDp1CmXLlsWYMWPE9bKaTBl7e3vExMSgS5cu4rKYGNUfOkWVXLxwHt5eDcTHISNymxh06twVkX+uVFBU3y+gTVs8f/YMEyLG4emTJ6jk4oqdu/+Bqanpl5+spGbNnocJ4WMRPLg/nqWkwMzMHN17BiF0zDhFh/Zdkh8mo2vnDnj54gWMS5ZEzZq1EX38NEqWLKno0L7Lz1oud3cPbNy8DePDRmPq5ImwsrLGjFmz0a6Dancie5aSgh6BXfDk8WMYGhrCuWIl/LVnHzy9Gik6tE8y1NPBhP6+KG1SDC/fvMPOw5cxftEe5Ehy72Lsir6CgVO3YEQ3T8wa1hIJ91PQPmQlTsUlAQByJFL4BUdi0oBm2PJ7D+gV0ULigxfoGb4B+07FK7JoX6TMx3iBVH3aCgXp1q0bnj59ihUrVgDIHTR3wYIFWLx4MQ4fPow3b97A398fa9asgYeHB/7++29ERERAIpHg9evXAHI77/Tq1QuLFy9GzZo1ERUVhZkzZ8LGxgaXLl366ljevHkDQ0NDPHn+utBvi/9ogqC8tyNYfh/eUvpZ8NeQKdrPeiw0qjH0yxupoFenf1d0CAXuzZs3MC1hiNTU1M/mGlxj+R3++ecfmP2vvZC+vj4cHBywefNm1K9fHwAwZMgQDBgwAJmZmfD19cXYsWMRHh4uPr9jx464c+cOhg8fjoyMDLRp0wbdunXDOSWZlokxxhhj7FtwjaWSadSoEUqVKoU1a9Z89XO4xpIpC66xZKxw/KzHQq6xVB1cY6kC3r17hyVLlsDb2xvq6urYsGEDDh48iAMHDnz5yYwxxhhjSoYTSwUSBAF79uzB5MmTkZGRAXt7e2zduhVeXjxlImOMMcZUDyeWCqSrq4uDBw8qOgzGGGOMsQLBA6QzxhhjjLECwYklY4wxxhgrEJxYMsYYY4yxAsGJJWOMMcYYKxCcWDLGGGOMsQLBiSVjjDHGGCsQnFgyxhhjjLECwYklY4wxxhgrEJxYMsYYY4yxAsGJJWOMMcYYKxCcWDLGGGOMsQLBiSVjjDHGGCsQnFgyxhhjjLECwYklY4wxxhgrEJxYMsYYY4yxAsGJJWOMMcYYKxAaig6AFRxBECAIgqLDYL8wNTX+/qkKqZQUHUKh+Fm/gxnZEkWHUChenf5d0SEUCqM6oxQdQoGjnMyv2o5rLBljjDHGWIHgxJIxxhhjjBUITiwZY4wxxliB4MSSMcYYY4wVCE4sGWOMMcZYgeDEkjHGGGOMFQhOLBljjDHGWIHgxJIxxhhjjBUITiwZY4wxxliB4MSSMcYYY4wVCE4sGWOMMcZYgeDEkjHGGGOMFQhOLBljjDHGWIHgxJIxxhhjjBUITiwZY4wxxliB4MSSMcYYY4wVCE4sGWOMMcZYgeDEkjHGGGOMFQhOLBljjDHGWIHgxJIxxhhjjBUITiwZY4wxxliB4MSSfbUlixbC3s4KxfR0UKdmNcScO6fokAoEl0u1cLlUx9u3bzFiWDAcylmhhGERNKxXCxfOxyg6rO9y4vgx+Ps1h7WlOXQ1BezauUPRIX2z5X8sQa2qlWFpagRLUyM0rl8LB/btldvm3NnTaNHEC6WNDWBpaoSmjerj/fv3Cor4v1PV/aVXRAszg5vh5rYQvIyeiCN/9EUVxzLi+j/CAvD+9DS5v52zA+VeY/OMLkjYPgqvoifizl+jsXxcG5gZ6xd67D9FYhkeHg5XV9dPrl+5ciWKFSv2Xe/RrVs3+Pn5fddrqLLNm6IQMmIoxoSNx+lzF1Gpkgta+HojJSVF0aF9Fy6XauFyqZb+fXrhyKGDWPbnapy7cBmeXo3QrEkjPEpOVnRo/1l6ejoqVnLBnHkLFR3Kf2ZeujTGT5iMIyfP4fCJs6hTrwE6tmmF+OvXAOQmla1/80UDz0Y4eOw0Dh0/g159+kNNTfVSBlXdX4tD/dHQoxy6T9gE905zcPDsLfw9ryfMSxqI2+w7fRNWvpPEv67jNsq9xrGLd9ApbB1c2s1Ch9FrYVOmBNZP6VTosQtERIX+Ll9w+vRp1K5dGz4+Pvj777+/+fnh4eHYsWMHYmNjP7p+5cqVCA4OxuvXr/9zjN26dcPr16+xY8eO//waX6N+/fpwdXXFnDlzvvo5b968gaGhIZ6+SIWBgcGXn/Af1KlZDVXcPTBn3gIAgFQqhZ21Bfr2H4gRI0cVynv+CFwu1cLlKjhSaeEe+t+/fw/TEgbYtGUHfJr6istrVXdHY28fjI+YVCjvq6YmFMrrfoyupoCoLdvR4je/Qn+vjGxJob6+demSmDB5Ojp3645G9WqifkMvjBk/oVDfEwB0NNUL/T1kfuT+Mqrz33+3OtoaeHYwAgEhq/HPqZvi8pMrBmD/6QRE/LEff4QFoJieDtqMWvPVr+tb2xGbpneGYd0w5Eik3xwX5WQi8/wcpKZ+PtdQisuP5cuXY+DAgTh27BgePXqk6HDYB7KysnDp4gU09PQSl6mpqaFhQy+cO3NagZF9Hy6XauFyqZacnBxIJBJo6+jILdfV1cXpUycVFBX7kEQiwdbNUXiXng6PatXxLCUF52POoaSJCRo3qI3yVubwbdwAp0+dUHSovwwNdTVoaKgjIytHbnlGZg5quliJj+u42eDe32GI2zgMc0f4obhBkU++ppGBLtp5u+LMlfv/Kan8FgpPLNPS0hAVFYW+ffvC19cXK1eulFsfHR0NQRBw6NAhuLu7o0iRIqhZsyZu3rz58RcEkJiYCBsbGwwYMACfqpDduXMn3NzcoKOjAxsbG0RERCAnJ+ej2+YVERGBkiVLwsDAAH369EFWVpa4LjMzE4MGDYKJiQl0dHRQu3ZtxMTItyc6evQoqlatCm1tbZiZmWHUqFHi+3br1g1Hjx7F3LlzIQgCBEHA3bt388WQmZmJN2/eyP0VpufPn0MikcDExFRuuYmpKZ48eVKo712YuFyqhculWvT19VGteg1MnzoJjx89gkQiwYb1a3H2zGk8efxY0eH98q5dvYIyJQ1hWqwIhg7qhzUbt8DB0Ql3794BAEybPAFdA3tiy46/4eJaGX5NGyPx9i0FR/1rSHuXhTNX7iE00BNmxvpQUxPQztsV1ZwtUapEbhvJA2duoueETWg6KBJhi/aiTmVr7JwdmK/GflI/Hzw/PAGP9o2HhWkxBIxcXejxKzyx3LRpExwcHGBvb49OnTrhzz///GgyOGbMGMyaNQvnz5+HhoYGunfv/tHXu3z5MmrXro0OHTpgwYIFEIT8t0WOHz+OLl26YPDgwbh+/TqWLl2KlStXYvLkyZ+N9dChQ4iPj0d0dDQ2bNiAbdu2ISIiQlw/cuRIbN26FatWrcLFixdhZ2cHb29vvHz5EgCQnJyMpk2bwsPDA3FxcVi8eDGWL1+OSZNybwnNnTsXNWrUQK9evfD48WM8fvwYFhYW+eKYOnUqDA0Nxb+PbcMYY4q27M/VICLYWZeBkb4OFi+cj4C27VWyrd7Pplx5exw7cwEHj55C91690S+oO27EX4dUmlub1a17L3Ts0g2VXCtjyozfYVfeHmtXr1Bw1L+O7hFREATgzl9jkHp0Evq3qYVNB+Ig/V9+tPngZfx9Ih7XEp/ir2PX0Wr4Krg7WaCum43c68xedwzVu86D76BlkEgJy8a1KfTYFf7rXr58OTp1ym1M6uPjg9TUVBw9ejTfdpMnT0a9evXg5OSEUaNG4dSpU8jIyJDb5tSpU6hfvz6GDx8uJmsfExERgVGjRqFr166wsbFBo0aNMHHiRCxduvSzsWppaeHPP/9EhQoV4OvriwkTJmDevHmQSqVIT0/H4sWLMXPmTDRp0gROTk6IjIyErq4uli9fDgBYtGgRLCwssGDBAjg4OMDPzw8RERGYNWsWpFIpDA0NoaWlhSJFiqBUqVIoVaoU1NXztz8JDQ1Famqq+PfgwYMvfs7fw9jYGOrq6khJeSq3POXpU5QqVapQ37swcblUC5dL9djY2mLfwWikvHyLm4n3cezkWeRkZ8PK2ubLT2aFSktLCza2dnB1q4LxE6bAuWIlLFk4H6VKmQEA7B2d5La3t3fAw0I+17B/JSW/RON+f6BEg7Eo5zcNdXoshKaGGpKSX350+7uPXuLZqzTYlikht/xF6jvcfvAch2Nuo8vY9WhSywHVnC0LNXaFJpY3b97EuXPn0L59ewCAhoYG2rZtKyZieVWqVEn8v5lZ7hc/b4/J+/fvo1GjRhg3bhyGDRv22feNi4vDhAkToKenJ/7JagnfvXv3yee5uLigSJF/2zDUqFEDaWlpePDgARITE5GdnY1atWqJ6zU1NVG1alXEx8cDAOLj41GjRg25WtRatWohLS0NDx8+/GzMeWlra8PAwEDurzBpaWmhslsVHDl8SFwmlUpx5MghVK1eo1DfuzBxuVQLl0t1FS1aFGZmZnj16hUOHtiHZs1bKDok9gGpVIqsrExYlrWCmZk5bifINze7fesWLCwKNyFh+b3LyMaTF29RTF8XXtXKY/fx6x/drnRJA5QwLIInz99+8rVkt8m1NDUKJVaZwn31L1i+fDlycnJgbm4uLiMiaGtrY8GCBTA0NBSXa2pqiv+XJWayKnsAKFmyJMzNzbFhwwZ07979s8lWWloaIiIi0KpVq3zrdD5oaM5yDQoeil7du6JKFXe4e1TFgnlz8C49HV26Bn75yUqMy6VauFyq5cD+fSAilC9vj8TE2xgTOhLl7R3QWYXLlZaWhsTbt8XHd5OSEBcbC6PixWFpqRqJV8S40fBq7AMLC0u8ffsWWzZtwIljR7F11x4IgoCBQ4Zh6qQIOFdyQcVKLtiwdjVuJdzAqvVRig79m6nq/vKqVg6CICDh3jPYlimBKQOaIuHeM6zefR5FdbUwpocndhy5iicv0mBTpjgm92+CxIcvcOBsAgDAw8kCVZzK4FTcXbx++x7WpUtgfFAjJD58jrNX7xVq7ApLLHNycrB69WrMmjULjRs3llvn5+eHDRs2oE+fPl/9erq6uti9ezeaNm0Kb29v7N+/H/r6Hx8I1M3NDTdv3oSdnd03xRwXF4f3799DV1cXAHDmzBno6enBwsICxsbG0NLSwsmTJ1G2bFkAQHZ2NmJiYhAcHAwAcHR0xNatW0FEYnJ88uRJ6Ovro0yZ3IFPtbS0IJEU7rAS/0VAm7Z4/uwZJkSMw9MnT1DJxRU7d/8DU1PTLz9ZiXG5VAuXS7W8eZOK8WGjkZz8EEbFi8PPrxXGT5gsV1Ggai5eOA9vrwbi45ARQwEAnTp3ReSfKxUU1bd5nvIMfXsG4umTxzAwNEQF54rYumsPGng2AgD0HTAYGRkZGD1yGF6/eokKFSth2+5/YG1jq+DIv52q7i9DPR1M6OOD0iaGePnmHXZGX8X4JfuQI5FCQyqFs60ZOjapgmL6Onj8/C0Onk3AhD8OIOt/w1K9y8zCb/WcEdbTC0V1tPDkxVvsP5OA6SsPi9sUFoWNY7ljxw60bdsWKSkpcjWTABASEoLDhw8jJiYG0dHRaNCgAV69eiUOch4bG4vKlSsjKSkJVlZWcuNYpqWloUmTJiAi/PPPP9DT08s3juW+ffvQrFkzhIWFoXXr1lBTU0NcXByuXr36ybaZ3bp1w9atW9G8eXOEhYXh7t276N69OwIDAzF16lQAQHBwMDZv3ozly5fD0tISM2bMwK5du5CYmAgjIyMkJyejfPnyCAwMxIABA3Dz5k307NkT/fv3R3h4OAAgKCgIsbGx2LRpE/T09FC8ePEvNnT/EeNYMsZ+LoU9jqWi/MhxLH+kwh7HUlF+5DiWP9L3jGOprJR+HMvly5fDy8srX1IJAP7+/jh//jwuX778za+rp6eHvXv3gojg6+uL9PT0fNt4e3tj9+7d2L9/Pzw8PFC9enXMnj1brGn8FE9PT5QrVw5169ZF27Zt0aJFCzEhBIBp06bB398fnTt3hpubG27fvo19+/bByMgIAFC6dGns2bMH586dg4uLC/r06YMePXogLCxMfI3hw4dDXV0dTk5OKFmyJO7fv//NnwFjjDHGmCIoxcw77PtwjSVj7FtxjaVq4RpL1cI1lowxxhhjjH0nTiwZY4wxxliB4MSSMcYYY4wVCE4sGWOMMcZYgeDEkjHGGGOMFQhOLBljjDHGWIHgxJIxxhhjjBUITiwZY4wxxliB4MSSMcYYY4wVCE4sGWOMMcZYgeDEkjHGGGOMFQhOLBljjDHGWIHgxJIxxhhjjBUITiwZY4wxxliB4MSSMcYYY4wVCE4sGWOMMcZYgeDEkjHGGGOMFQhOLBljjDHGWIHQUHQA7PsREQDg7Zs3Co6EMaYqpFJSdAiFQk1NUHQIhSIjW6LoEApFlqa6okMoFJSTqegQChxJcsskyzk+hRPLn8Dbt28BAHbWFgqOhDHGGGM/s7dv38LQ0PCT6wX6UurJlJ5UKsWjR4+gr68PQSjcq/U3b97AwsICDx48gIGBQaG+14/E5VIdP2OZAC6XquFyqRYu1/cjIrx9+xbm5uZQU/t0S0qusfwJqKmpoUyZMj/0PQ0MDH6qH6cMl0t1/IxlArhcqobLpVq4XN/nczWVMtx5hzHGGGOMFQhOLBljjDHGWIHgxJJ9E21tbYwfPx7a2tqKDqVAcblUx89YJoDLpWq4XKqFy/XjcOcdxhhjjDFWILjGkjHGGGOMFQhOLBljjDHGWIHgxJIxxhhjjBUITiwZY4wxxliB4MSSMcYYY4wVCE4sGUPuVFUAcP/+fQVHwn5lRASpVKroMArMxYsXFR0CYz+dvIP5KOPxghNLxgAIgoAdO3YgICAA165dU3Q4hYJHFlNemZmZAHK/hw8ePFBwNAXj9OnTcHd3x8KFCxUdSqGRSCSKDqHAyY4TR48exYEDBxQcDfsYQRDw5MkTxMfHQ01NDVu2bMG2bdsUHZaIE0v2VZTxqqggyA6iDx48wNy5c9GzZ09UqFBBwVEVDFnZrl+/DolEAkEQFBwR+5jExESMGTMGr169wubNm2FtbY3ExERFh/XdatSogUmTJmHo0KFYvHixosMpELLj4Nu3bwEA6urqiI2NxZMnTxQZVoGQHS8EQcCRI0fQtGlTpKenIycnR8GRfb8Pz1+qfpGdmpqKDh06YPbs2Zg7dy7atGmD9PR0RYcl0lB0AEz5SaVSqKnlXoP89ddfSE5OhpWVFcqVKwdbW1sFR/d9BEHA8ePHsXPnThgaGuK3335TdEgFRhAE7Nq1C0OHDsXq1atRs2ZNRYf03YgIgiDgzJkzSE9Ph6enp6JD+m5XrlzB0qVLce3aNURHR2PFihWwtbUVy6rKRo8eDXV1dQwYMAAA0LdvXwVH9H3U1NTw6NEjBAUFoX///sjKykLLli1x9uxZlCpVStHhfRfZd+3Ro0c4f/48Ro8eDT8/P5VPwgCI56/Y2Fi4urqq/O/K0NAQPXr0QHh4OJYtW4YpU6agc+fOynPMIMa+0siRI0lPT48qVapExYoVo7p169KqVasUHdZ3+/3330kQBDI0NKQLFy4oOpzvJpVKiYjo0aNH1LJlS1q0aJGCIyoYsnJt3bqVzM3NqU+fPvTw4UMFR1UwQkNDSRAEatiwoVyZZGVWddOmTSM1NbWf4rt46dIl8vf3pwoVKpC2tjatX7+eiIgkEomCI/s+UqmUkpKSSBAEKl68OM2cOVPRIX23vPvk+PHjZGJiIu4vVSU7Jty9e5esrKzIwsKC+vfvT1evXs23jaLwrXD2VWJiYnDw4EHs27cPcXFxOHDgAMqXL4+5c+ciKipK0eF9lyFDhiAyMhJqamr4888/cffuXUWH9F0EQcCxY8cwfPhwvH79Gg0aNACg+rd/BEHAgQMH0KlTJ0ycOBGzZ89G6dKlFR3Wd5G10dPR0cGQIUNw69YtTJ48GTdu3ACQW2ZV328AEBISgsmTJ2PAgAEqe1uc/texytXVFc2aNcP169dhaWkJfX19ALm1YqraZIj+V9NlZWWF2bNn49WrV7h06RKeP3+u6ND+s7x32tauXYv169cjPT0dISEhWLdunYKj++9kNZImJiY4fPgwJk6ciFOnTmHu3Lli/wCF11oqNK1lKmHatGnUvXt36tixo9wV4NWrV8nf35/atWtH2dnZCr9K+hqyGBMSEujcuXN08OBBcd28efPI3NycRo8eTffu3VNUiAXi8OHDZGxsTGpqarR161ZxuSrso0/JzMykvn370rBhw4iI6PXr1xQTE0PBwcE0btw4unHjhoIj/H4bNmygMmXKUJ8+feTKExcXp8Covp7s+3Xt2jU6fvw47d27V279lClTVL7mcuPGjdS8eXNatmwZdezYkWrXrk1RUVHielWquZTtrw9jnjVrFgmCQNOmTaPU1FRFhFZgQkJCqFSpUrR48WKaNm0a1alTh8qVK0crVqxQdGjfRLav7t27R9evX6fExERxXWRkJFWuXJl69+4t1lxOnDiRtm/frohQiRNL9kVjx44lQRDI2tqa7t+/L7du/fr1pKGhQXfu3FFQdF8v761UBwcHcnBwICcnJ3Jzc6MHDx4QEdHcuXOpdOnSNHbsWEpKSlJgtN/v5MmTZGVlRc2aNaPz58+Ly1U5uWzfvj1VrlyZkpKSqHPnztSwYUOqWbMmlSxZklq1aqXo8L6K7POPiYmhtWvX0oIFC+jevXviyX3Dhg1kYWFBffv2pWPHjtGECRNIEAR6+fKlUu87WWzbtm0jCwsLqlChAunr61PLli0pPj5e3G7KlCmkra1Ns2bNUlSo30xWttu3b5Oenh7Nnz+fiHL3YZs2bah27dq0efNmcft9+/bRkydPFBLr15KV6fDhwzR48GDq3r07hYWFietnzpxJgiDQ9OnTVTa5vH37Njk4OMglWLGxsdSrVy+ysbGhDRs2KC64b5D33OXo6EhmZmZkZ2dHLVq0oMzMTCLKTS6rVq1K9evXp7Zt25IgCApr2sWJJZPzqavtuXPnkiAINGHCBHr+/Lm4/OzZs+Tg4EA3b978USF+l6NHj5Kenh5FRkZSRkYGHT16lARBoCVLlojbzJs3j3R0dGjixImUnZ2twGi/juygc/nyZdqxYwetW7eOUlJSiCi3vNbW1tShQwe6ePGiIsP8ZrJynT9/XqxZPnXqFFWuXJm0tbUpICCAtm3bRkS5yYyrqyu9fPlSYfF+jbwniOLFi1PDhg3J1NSUvLy8aMWKFZSTk0NERJs2bSJHR0dydnYmCwsLOnfunCLD/qy8ye7+/fupWLFiFBkZSUS5FzeCIJCvry9duXJF3C4sLIxKlChBr169+tHh/mfHjh2jlStXUmhoqNzy8+fPU9u2bal27do0e/ZsCg8PJ0EQVKL977Zt20hPT4/69+9PI0aMIDs7O3J1daWsrCwiyq251NLSovDwcHrz5o2Co/12Dx48ICMjI1q9erXc8kuXLpGVlRWZmZnRmjVrFBTdtzly5Ajp6urS4sWL6dChQ7RlyxaysbGh6tWri8eNqKgoGjx4MLVq1Uru9/ajcWLJRHmTyjt37tDVq1flkkhZzcmwYcMoOjqarl69Sj4+PuTh4aEyt39mzZpF/fr1I6LcMpYtW5b69u2bb7tFixZRQkLCjw7vP9uyZQuVLVuW3NzcqEaNGqSnp0eHDh0iIqLo6Giytramzp07K3WCklfeBMzCwoKGDx9OycnJlJ2dTenp6fnKMWjQIGrSpAmlp6crItxvEh0dTaamprRs2TIiIrpy5QppaGhQ1apVacmSJeJv6cqVK3TmzBmxNl3ZbNu2ja5fv05EufvrzZs3NGjQIAoPDyei3N+XjY0NdezYkczNzalBgwYUFxcn7tu8xxZlExwcTDNmzBAfp6amko+PDwmCQC1btiQikrvovHTpEgUFBZGDgwNVqFBB7g6BskpOTiZnZ2eaN28eERElJSVRqVKlqGfPnnLbRUREkJGRkVLvL6J/jxl5/33+/Dk1atSIhg0bli/+gIAAqlu3Lnl4eNCBAwd+eLzfKiIiIt9dmcTERLKysqKAgAC55bILA0XhxJIRkXytQ2hoKFWsWJF0dHSoVq1aYiJGRDRp0iQSBIEEQaCuXbtSq1atxC+xKiSXnTp1osDAQHrx4gVZWFhQUFCQWPaVK1eqZE/Is2fPkpGRkVhLdO3aNRIEgaZMmSLuk+joaDIwMKBevXpRRkaGIsP9av/88w/p6urS0qVL6f379x/d5vz58zRs2DAqVqyYSrRDzM7OpmnTplFwcDAR5Z4YZMmXj48P2djY0LJly8QaCGV1+fJlcnFxoZYtW4oXYJmZmbR9+3ZKSEigly9fUpUqVahHjx5ERLR7924SBIFq165N165dU2ToX5STk0PLli3LV8N/4sQJ8vf3JwMDA7HMeU/gr1+/pqdPn4p3C5Td9evXqVy5cpSVlUUPHz6kMmXKUO/evcX1u3fvFv//4sULRYT41fKeez5Mqn7//XcqVqwYzZ07V9w3b968odatW9OiRYuoVq1aNHr06B8a73/RtWtXcnd3Fx/LLmxWrFhBFSpUUKoLUE4smZzp06dT8eLFaffu3XTkyBGaOHEiOTs7y10pLViwgARBoHnz5tHr16+JiJTyRJi3ZuTdu3dElFvL4u3tTSVLlqRevXoRUe5BSSKRUP/+/alfv37itqpi3bp11KFDByLKrSWStc+Tefv2LRHl3sq7deuWQmL8VhkZGdS5c2caOXIkEeXWGF28eJFCQ0MpIiKCXrx4QZcvX6aBAwdS5cqVVSKplImPj6fr169TWloa1apVi7p3705EucOHFCtWjCpUqCDWZiqzP//8k+rXr0+tW7cWay5lFy2bN2+mqlWrim2vd+zYQU2aNCFHR0eVaru8Z88eGj9+vPg4JiaGGjRoQBYWFnT79m0iIpVoLpPX1atXSSKR0OPHj6levXq0detWsrS0pN69e4tlSUhIoE6dOtHx48eJSLnbZedNKhctWkRt2rShdu3a0dSpU8Xl48aNIxMTE2revDkFBQVRjRo1yM3NjYhyKxs8PT2VuoxERH///TfZ2trSxo0b5Zbv2LGDrK2tKTk5WUGR5ceJ5S8u748pNTWVfH196ffffxeXpaen08aNG8nJyYn+7//+T1w+efJkEgSB5syZo5TtpGTl2rVrFzVu3JgOHDhAEomEbt68SbVr1yZbW1vat28fEeXWNIwZM4ZKlSol18lAWX14AIyIiKCGDRvSvXv3yNLSkoKCgsSD7bZt2yg4OFjlkmUiog4dOlCdOnXo9u3bFBgYSA0bNiR3d3cqWbKkmEhfvXpVqTtJfOxkJTt5Hzt2jJydncUavJiYGPL09KTOnTsr9agEeROpP/74g5o2bUoBAQFyvVRnzJhBtra24r4JDQ2lqVOnqlQSJpVKadGiRSQIAk2cOFFcHhMTQ97e3mRlZSUmzsp4YU2UP+m9cuUKlSlThu7fv0+vXr2i+vXrk5qaGnXs2FFuu+HDh1P16tWV+rf1IVnv79GjR9Pw4cPJ2tqaAgMDxfVr166lIUOGUOPGjalv377iRVCrVq0oODhYae64yY4ZycnJlJiYKLYbf/r0KbVs2ZJ8fX3FTkdZWVk0atQoqlq1qlK1L+fE8hf24Q9JKpWSm5ub3K1votwvr7+/P7Vv315u+fTp00kQBFq0aJFSXu3JGqZPmDBBrF0gIrpw4QJVrlyZnJ2dycHBgby8vMjc3FylOrecOHFCvCI/deoU1a9fn4oXLy4eSGX7Njg4mDp06KD0De8/9v3ZuXMneXh4kLq6OgUEBNCWLVuIKLfJgoeHh9K3p5SV6cSJEzR9+nQaNWoUHTx4UDyhHThwgKytrWnnzp0kkUho/Pjx1KNHD7GGWVl92JvY2dmZ1NXVqU2bNuIt4oSEBDIwMKBKlSpR3bp1ydDQkGJjYxUZ9n/y7t07Wrp0KampqYltR4mIzp07R02bNiUDAwOlrYGdOXMmtW7dWu53cvr0aXJwcBBvF1+7do2MjY3J19eXVq9eTfv376cBAwaQoaGhSt0FWL9+PZUvX57OnDlDRLk15kWKFBFHJZDJe85LSUmhMWPGUPHixcUad0XLO7JCuXLlyNramgwNDWngwIF0584dSkpKotatW1PZsmXJ3t6eGjRoQEZGRkp37uLE8hcVExNDz549I6LcGXVWrlxJREQDBw4kb2/vfD+08ePHk5eXF2VkZMj9OGfPnq00P8q8kpKSyNbWlhYsWEBEuQeUrKwsOnv2LL1//55evHhBu3btopEjR9KGDRtUYrgkmczMTAoODqaGDRsSUW57IVkHiWXLllF2djY9fvyYQkNDydjYWOnbtOVNwMLDw2nUqFFiL863b9/SqVOn5Lbv27cvNW/e/JPtLpXJli1bSE9Pj+rVq0fVqlUjQRBo+PDh9ODBA3rx4oU4pp6Tk5NSniA+Zf/+/SQIAs2ePZv++usvCgkJoYoVK1Lr1q3FWv8rV65Qr169aMSIEUr/HST6t9bx4cOHcncupFIpLVy4MF9yeerUKfL391fa5iX//PMPaWtry12s7N27l1xcXIjo3yTrwoUL1LBhQypbtiw5OjqKnayUWWZmplzCvHjxYho3bhwR5d6lMjIyojlz5lBkZCSpq6uLbX1lXrx4QYGBgWRjY0OXLl36kaF/UXR0NOnq6tLs2bPpwoULNH/+fKpRowa1bNmSkpKS6Pnz53Ts2DEaPnw4zZ8/Xyk7mXJi+QtKSUkhQRBo4MCB1Lt3b9LX1xeHJoiNjSVTU1Pq3LmzOAbW27dvqX79+mKbRCLl7agjS1Ju3LhBVapUoQsXLtDz589p5syZVK9ePTI0NKS6devSyZMnFRzp9zl//jxpa2uLt0RevXpFvr6+VLFiRSpWrBjVrl2brK2tVSZR2bp1KxkaGlKHDh2oe/fuZGRklK+G/OrVqzR06FAqVqwYXb58WUGRfr1bt26RpaUlRUZGit/LDRs2kLGxsTjI+71792jp0qU0d+5cpTxBfEgqlZJEIqGePXtSu3bt5Nb98ccf5OjoSG3atBGTrZycHKW8myGzaNEiOnz4sHjLePPmzWRhYSGOw3n48GGxdk+WXOa9La7sFzdHjhwhPT09CgwMJIlEQjt27CBXV1cikr9LkJGRQU+ePKGUlBSlrzHfsmULtWrViipXrkwTJkwQl9+5c4eeP39Obm5uNG3aNCLK/Q2WLl2aBEGgkJAQude5d+9evnGZFUm2P4YNGyZXy0r0790bWZtzZceJ5S/m6NGjlJSURBcuXCBtbW3S1dWlw4cPE9G/V+xnzpwha2trcnNzI2dnZ6pWrRo5OzuLB1hlPlHIbvneu3ePihcvTt7e3mRqakp+fn40depU2rdvHzk6OqrUzB95P2+JRCI+Hjp0KHl6eooHx/T0dDp//jwtWbKEjhw5olS9BD9H1jNaVrt869YtKl68OAUFBYnbnD17lvr06UMuLi5Ke0s1JSWFYmJixAuyK1eukI2NDcXGxsrtw3Xr1pGamhodO3ZMUaF+t/79+5OXl1e+HrjBwcGko6ND3t7eSj22rWx/2Nvbk6WlJZ06dYouX75M1tbWNHPmTDpy5Ah5e3uTpaUlbd68WRyEesmSJeKg4ari0KFDpKenR4MGDaJNmzZRjRo1aP/+/RQdHU3Xrl2jCxcu0K5du+jx48eKDvWLlixZQgYGBjRkyBAKDg4mdXV1Wrhwobj+7NmzZGlpKV6k3bp1izp06EAHDhyQawerzOewoUOHkpeXF+Xk5MhV4MyYMYOMjY2VPvEn4sTyl/LmzRvq0aMHjRw5kk6fPk06OjqkpqZGQ4YMoUePHhHRvz+4W7du0YYNGygkJIQWLFggXtErc+P72NhY0tbWptOnTxNR7jR4o0aNolmzZsk1Qvfy8qK5c+cqKsz/5MCBA7R9+3a5jlI7d+4kOzs7seemqrp48SJVqlSJiHIvCGRTGsrExMQQUW4trex7qmyuXbtGtWrVIh8fH2rVqhXl5ORQTEwMaWpqiu2+8g7z5OzsLNcZTtXMnDnzozXiq1evpooVK1L79u2V9sLmw7st9erVIwcHB1q1ahWNGDFCbp2/v3++5HLZsmVK2fwnrw8Tp4MHD1LRokWpSJEiZGtrS9bW1mRmZkb29vZUpkwZMjc3V/rmQJGRkaSpqSk3i0779u1p3rx54vE9MTGRbG1taeDAgXT9+nXy9vamli1bip+Hsnayymv27Nmkp6cnTs0oi33//v3k5ORET58+VWR4X4UTy1/MunXrqGzZsmL7ygMHDpCamhr179//i1esyv6jvHv3LjVr1owMDAzo7NmzRCR/Ms/JyaHQ0FAyNTWV68yj7N69e0cDBw4kQRDIz89PvM1DRNS5c2e5sc1UgexAeeTIETp48CBdv36datasSQcOHMg37ElcXBx16tRJqecBv3r1KhUrVkycYz5v4hIQEEBOTk5yPaYzMzOpSpUq9Mcffygi3G8i21fx8fEUFxcn1wTBw8ODKlSoQDExMWJ7t5EjR1JoaKjSjnso2zdJSUk0f/588ThQtWpVEgSBvL2989XC+vv7k62tLa1du1bhA09/iWx/vXnzhtLS0uTWHT16lEqWLElNmzal+/fv04sXLyg1NZWeP38uDhunrI4cOUKCIFBERITcchcXF6pUqRLp6+tTrVq1aN68eTRr1iwqU6YMlS1blqpVq6a0d9pkx7jExESKj4+XO8bJRh2Ii4sTf1vBwcHk5uam9PuKiBPLX0beH1WnTp2odevW4vyvf/31F6mpqdGgQYPEachat25NUVFRCon1a+Utk+z/9+7dozZt2pCurq44+4VEIqE///yT/Pz8qHTp0irT7vBDp06dotGjR5OpqSlVrVqV5s2bR9u2bSMvLy/666+/FB3eF+XdX0eOHKEiRYrQtm3bKDExkdzd3UlHR4e6du0q95yhQ4dSgwYNxAshZfPixQuqXbs2DRo0SG65LIE5ceIE+fj4kL29PR06dIiOHj1KY8aMIWNjY7lkU5lt3ryZTExMyMLCgmxtbcXRCN6/f09Vq1Yla2tr8vDwoMaNG5OWlpbSdtSR7ZPLly9T+fLlqWXLlnK1X40aNSIjIyM6dOhQvovoRo0aUcWKFZV6dAXZ7+vvv/+m+vXrk5ubG9WtW5euXr0q1rYePnyYihQpQn369FGpIcgSEhKoTp061KJFC/EORqtWrcjOzo6ioqJo7969VKFCBXJ3d6e4uDhKTk6m06dPi/tcWe60rVq1SpzIgoho48aNZGFhQSYmJmRnZ0dt2rShrKwsSklJIR8fH9LX1ycPDw9q2LAhGRoaKl1Ho0/hxPIn97FONkeOHKGWLVuKt4yJcmdZ0NbWpsaNG5ObmxuVL19e6a/OiXKvwmW3cGQH1rt371KbNm2oSJEi4g/xypUrNGTIEKVu9yUjK0dcXBxt376dNm/eLDebR0pKCvXq1Ys8PT1JV1dXnGZT2a7IP+Xhw4c0c+ZMmjRpkrhsz549pKGhQUFBQbRv3z46f/48BQcHK31HnWvXrpGtrS0dPXr0kx3azp07Rx07diRtbW2ys7OjChUqKP3Fjey79OLFC3JwcKAVK1bQ4cOHaerUqaSpqUlhYWHitosWLaIxY8bQiBEjlP4WcXx8PBkZGdGoUaM+OqB0rVq1yMrKio4fP55vfyrrrf28du7cSfr6+jRmzBg6dOgQ1axZk1xcXGjPnj1icnno0CESBIH69++vMscMotzk0sfHh3x9falWrVrk5uYmN9TThQsXSBAE2rlzp9zzlKWjaUpKCjVr1oyqVatGGzdupEePHpG1tTUtXryYDh8+TBs3bqQyZcpQw4YNxf0SGRlJkyZNokmTJqlE5z4ZTix/YnnbzPz+++/isC3Z2dnUvHlz8vf3l9s+OjqahgwZQiNGjFCJNpWpqank5eVFxsbG4gFG9oNMSEggV1dXKlmypHiFq8xl+ZCslqhcuXJkaWlJJUqUoL/++kvshSqVSik5OZlmzJhBLi4uYq9+ZXfnzh0SBIEMDQ3zdYCIiooiNzc3KlGiBDk7O5OHh4fSdtSRWbduHWloaIjfu7wnMVmtV3p6OsXHx9OzZ8/o3r17Slv7+qGDBw/SqFGjaMCAAWJS8vbtW1qwYAGpq6vnmwZP2ZOU9+/fU0BAAPXv319ueVZWFt25c0e8ePPx8SFLS0s6efKk0iQlX+POnTvk7u5Os2fPJiKiZ8+ekbW1NZmYmJCJiQnt2bNHbBp09OhRlZgM4kMJCQnk5eVFhoaGtGnTJiL6t0PjhQsXyMnJiU6cOKHgKD8tNjaWOnXqRA0aNKAhQ4ZQx44d5Spw4uPjydzcnDp16qTAKL8fJ5Y/qdjYWBIEgXbs2EGDBw+m4sWLy4239vjxY3JwcBDHr/xY42ZVSMROnz5NTZo0IWtr63yNz7t27UpqampkZmZG79+/V5mTxMWLF8nIyIhWrFhBT548oSdPnlDPnj1JT0+P9u7dS0TyJ3FlHig8PT2dnj17RkeOHBGbWaxfv54EQaA2bdrkm1f5yZMnFB8fT3fu3FHKGZ0+dPLkSdLR0REHb/+YefPmUaNGjVRmjnai3HagY8aMIXV1dapSpYrcOllyqaOjIw6bRKT8iWV2djbVqVOH5s+fLy77559/KDg4mAwMDKhMmTLUunVrIspNLg0NDcWOV6rg5s2bNH36dEpLS6NHjx6RnZ2dOLWrh4cHubi40I4dO8SLBFV1+/Zt8vb2piZNmsiNrNCsWTOqX7++0h/nY2NjqWPHjmRtbU3Vq1cXl8vOt8uXLycnJye6d++e+JtS9t/Whzix/IlFRESQrq4u6enpyd1OzMnJoezsbIqIiKABAwbQu3fvlP7HSPTvjysrK0uuYfqVK1fI09OTrK2t6e7du+Ly4OBg2rRpk1L3otu/f3++TlPbt28nNzc3evXqldwBJTAwkMzMzMSES9kPOjdv3qQuXbqQg4MD6ejokL6+PrVv356Sk5Np27Zt4lR5qtAY/VMePnxIJiYm1KJFC7nvXt59MmzYMBo1apTS7qe88sZ49+5dioiIEGfXyistLY1mzpxJJUqUoGfPnqlE2VJTU8nBwYF69epFN27coClTppC9vT35+/vT3Llzafny5VS2bFlxnEpPT0+lHfz8U2Tx9uvXj/z9/cWhaTp37kyCIFD58uXzdepRRbLb4k2bNqXjx49Tq1at5JpvKfv57MqVK9SuXTsqUqQILVmyRG7drl27qEyZMko9reuXcGL5k8n7g5o0aRIJgkAaGhq0devWfNuePHmSTE1Naffu3USkvAkKkXzD9JYtW5KLiwv17NmT9uzZQ0RE169fJy8vLzIyMqKxY8dS586dyczMTGmH0JDNWy5r65S35i4yMpKKFCkiXsHKarpu3bpFZcqUoYMHDyok5m8RFxdHZmZm1KdPH1q5ciXFx8dTSEgIWVtbk729Pd2/f1+suZwyZYrYkUwVbd26lbS1talz585yHVfS09MpNDSUypYtq/Rte2W/rw/vUty/f59Gjx5Nenp6+U6A6enpSjU/8dc4dOgQaWhoUNmyZUlfX5+WLFkiJmNZWVnUuHHjfAPzKyPZ/kpMTKSbN2/mq1lt2rSp3IDgQ4YMoUuXLol3DX4GCQkJ5OvrS5qammRvby8mlapwp40o95zVvn17qlatGi1evJiIci/YRowYQQ4ODirTZOZjOLH8SUVERFBQUBBdvXqVIiIiSFNTk9auXUtE8snnkiVLyNXVValmIPiUv/76i7S0tGjw4ME0YcIEcnd3pxo1atC8efOIiOjRo0c0ePBgcnd3p0aNGil1DzpZk4MtW7aQpqYmDRo0SByL7dmzZ1ShQgXq1auX3O1T2TSV0dHRCon5a8XFxVGRIkUoNDQ030E+KiqKKlWqRFWrVqWMjAxasmQJaWpq0tixY1U2uZRIJLRkyRLS0NAgBwcHCgwMpL59+1KLFi3IxMREZTrqHDp0iLp160YdOnSQS0oePHhAY8aMIX19fbkerarq/v37dP78+XwnbolEQgEBARQWFkYSiURpa73yzift6OhIzs7OZGpqSh06dBA7ePj5+ZGjoyP9+eef1LdvXzI0NFTpGrBPiY+Pp4EDB6pEn4CPuXz5MrVv3560tbWpcuXK1L59e3JwcBBHNFFVnFj+JPK2jdy/fz+VK1dOnAGEiCg0NJQ0NTXFKQCJcq9iV61aRf7+/rR///4fGu+3kEqllJqaSg0aNJCbwislJYX69+9P1atXl6vFS01NVeqp1v78809au3atGOP27dvFKTafPn1KEomE5syZQzVq1KDAwEBKTU2lhw8f0rhx48jKykqpax3u379PxsbGFBAQIC6TSqVyB/w//viDihYtKo7jOHnyZDIyMqLnz5//8HgL0tmzZ6l169bk6upKderUoZCQEKXvyZk3STEwMKBevXpRSEgIWVlZUYsWLcTjyoMHD2jcuHEkCAKtWLFCgREXjszMTAoLCyNzc3Ol32dEucMG6enpUWRkJKWlpdHevXtJEARav349EeXWJtepU4ecnJzIxcVFqS+yC4oyJpVf01zp+vXr1LFjRzI1NaXw8HCVrqmU4cRSxX04Ft769etp8ODBNGTIECKS/7GNHj2aBEGgQYMGUc2aNcnZ2ZmIcnsgy3pOKwvZnMREuQOE5+TkkIeHh9j+Sbbu+fPnVLFiRQoODlZYrN9CVg5XV1faunWrWCMpSy779etHaWlp9P79e5o/fz5VrFiRNDU1ydnZmUqXLi13saCMkpKSyMPDg1q0aJFvRqC8B9e6deuSn5+f+FjVbql+irJPIiD73eStjYuNjaXy5cuL7SiTkpLIzMyMBEGg2rVri8eQu3fv0qRJk5R6sPr/Ys2aNTRo0CAyNTVV+tplmfDwcHF2qtu3b5OdnZ3cFKgyjx8/Vtk7AapMdqxLTU2lrKwscfzTTyWYly5doqCgIJUY0uprcGKpwrp160bh4eFE9O+QC7Vq1SJBEMjT0/OjQ6DMmTOHvL29qXPnzkpbq5d3+IUNGzZQly5dKCkpierWrUuBgYFERHK3qoKDg8nT01PpT+qy/fHu3Tvy8fGhKlWq0ObNmz+ZXEqlUnr37h1t2bKFoqOjVeagI2tY7+3tLZdc5j2o1q9fnzp06PDRdarsY4P2K4u8s84sXbqUzp07R0S5Y4jKLkTv379PNjY21KtXL3GOaT8/P5Vrv/a1bty4QfXr16eWLVsq/RicMlKplHx9fWn06NGUkZFBpUuXpqCgIPH7Nm/ePLHmkv14sv2we/duat68Obm7u1Pz5s1p165dn32eKo0a8SWcWKqwnTt3igd8Wfu87OxsateuHZmbm9OKFSvE5DFvcpl39ghlGwT9ypUrFB4eThKJhJ49e0Y2NjbivN779u0jQRDyzbHcpk0bCgwMVNo2UXnJTszv3r0jT09Pcnd3p82bN+e7Ld6/f3+l7s3+JXmTy7zjykkkEnrw4AE1adIk31BXrPB8bNYZWac9otxaS6lUSn5+ftSxY0eSSqWUlpZG7u7uJAgCNW7cWFGhF7qnT5+q3MgEq1evptq1a5OxsTH17dtXrhKhR48e1L9//58qUVE1u3btIh0dHZo+fTpt3ryZAgMDSRAEpZ2VqqBxYqmCPjwRR0ZGUps2bcTbONnZ2eTr60uurq4UFRUljlv2YY2esp3QZWNvLly4kA4fPkwTJ06kPn36yA2PsXDhQhIEgdq3b09Dhw6l3r17k56enkoMEC77vGW3fdPT08nT0/OjNZdaWloUGBiYb5xHVfKpmsuQkBBycXFRmRrYn8WXZp15/fo1ubi4iNMcZmRkUM+ePenvv/9W2tEVfnayY8bDhw/pxo0b4uOLFy9S3bp1ycnJSZz4Ii0tjcaMGUPm5uZKPwrBz0h28Zaenk7NmzenGTNmEBFRcnIylS1b9qNNFX5WnFj+BBYvXkyVKlWioKAgueSySZMmVLlyZdq0aZPSX71eu3aNdHV1afz48URENHbsWHHcNdlYbDKHDx+mFi1aUMOGDalVq1ZKPeXfh86ePUtt2rQRhweRJZcf1lxGRUVR8eLFxZpoVZU3ubx48SJNnz6d9PT0lH5GnZ/N52adefjwISUkJFB6ejpVqVKF/Pz8KCkpiYYPH07ly5fPN84q+7G2bNlCFhYWZGFhQRUqVKAjR44QUe7QazVr1iQbGxuqXbs2NWzYkMzMzFSmnejPYNasWXLt+6VSKb1+/ZpsbGzo2LFjlJKSIjZVkFm1atVPn/hzYqlC8nZo+dDy5cvJzc2NevToIZdcNmvWjMzNzenQoUM/MtRvcuXKFTI2NiZHR0dxWUpKCs2YMYPU1NTEMb6I/q11lSXKytpO9FPWrl1Lrq6u1KlTJ7HDVN6ay61bt4pl+jChVlUJCQnUrFkzMjExIU1NTZUfSkMVfWnWmbJly1Ljxo1p27ZtZGtrS6VLlyYLCwtOUhREdpy/du0a2djY0MyZM+nIkSPk7e1NZcqUEWd6unLlCq1atYr69etHS5cupdu3bysy7F/K+/fvaerUqaSnp0djx44Vl+fk5FDnzp1p0qRJZGlpSb179xbPWykpKdSlSxdas2aN0t0xLEicWKqo3bt3044dO+jw4cPissjISDG5lA0vkZWVRcOGDVPaji2xsbFUpEgRql+/Ppmbm9PAgQPFda9evRJrLlevXk1Eucm17E/2WFl9KrYNGzZQ7dq1qV27dmIHivT0dPL29iZbW1vauXPnZ5+vim7cuEEtWrSgq1evKjqUX9LXzDrj6OhIwcHB9PTpUzpx4gTXVP5AH+utf/r0aVq1ahWNGDFCblt/f38xuVT16RlV3cuXL2nevHlUrFgxGjNmjLh81KhRJAgCNWnShN69eye33N7eXm6Wrp8RJ5YqYODAgXJz8gYHB5OJiQmVKlWKnJ2dadCgQeK6yMhIqlKlCgUFBdHZs2flXkfZksuYmBjS1NSk8PBwysnJoaVLl5KxsbFccvn69WsKCwsjQRDEAd6V2cdqlOPj4/PVJKxbt47q1KlDbdu2FS8C0tLSyM/P76dtz6ZsHcV+NZ+bdSYzM5MaNWpEXbp0UXCUv54Pe+vLjtuyjlM+Pj75fjv+/v5ka2srNx4u+3HyVm68ffuWZs+eTcWKFaPQ0FBxmw4dOpCJiQkNGDCAxo8fT926dSNDQ8NfYkxRDTCl9urVK2hoaGDv3r0oVqwYunbtinPnzuHAgQPQ1NTEvn37sGjRIqSnp2PZsmXo2bMn1NTUEB4eDmtra1StWhVEBEEQoK6urujiyHn37h369u2L8ePHAwDatm0LABgzZgwAYN68eTA0NMTw4cOhrq6Ozp07Q0NDQ9xO2UilUqipqSE5ORknTpyARCKBtrY2Fi9eDDs7O4wcORI2NjYAgA4dOiAnJwfBwcFQU1PD4MGDUa1aNWzfvl3BpSg8mpqaig7hl9awYUPcuXMHKSkpKFu2LIyNjcV1GhoaMDQ0hKWlJYgIACAIgqJC/WXIjhlXrlxB69atUaFCBZibmwMAYmJi0LRpU5w5cwbHjx9HvXr1xGP4li1b0LhxY8yYMQMtWrSAjo6OIovxS5CdR4F/fxsxMTEoVaoUunXrBkEQEBERAalUimnTpmHdunUICwvDjRs3cPbsWVSuXBknT55EhQoVFFmMH0PBiS37CsnJyRQeHk7Ozs7UunVr6tatm1j7+Pr1a1q8eDHZ2tpSz549xefs2rVL6WooPyfvgLIfq7l8+fIlTZ48WWnHmpPVOsTFxZGNjQ05OTmRpqYmVa1alVxcXMjb25sGDx6crzaydu3aZGJiQj179qT379//VLe/mWpQtVlnfjZf6q1fq1YtsrKyouPHj+e7I8IjK/w4jx49IqJ/+zokJiaSqamp2BHx5cuXNGfOHDIyMqKRI0eKz8vMzKSsrCyVOh9/L04slVjeg0hycjKNHz+erK2tqWbNmnLbvX79mpYsWUL29vbUqlUruXWq+GXOm1x+2ONOGeVNKosUKUIjR46k5ORk2rlzJzVp0oTq1q1L/fr1I1dXVxo8eLDYvub9+/fUq1cvmjx5Mp8gmEKo4qwzP5PP9da/c+eOONyYj48PWVpa0smTJ1VivN6fzebNm8na2loczYOI6MWLF+Tg4CA3xW7e5DIsLEwRoSoFTiyVVN6Dh2yg7CdPntD48eOpWLFi+b60qampNGvWLGrTps1PceBJTU2lyMhIEgSBQkJCFB3OF31sjmyi3KGgjIyM6OHDh7Rw4UJyd3entm3b0qpVqygkJIScnJxUfo5spppUcdaZn82XeuuXKVOGWrduTUS5yaWhoaFccsN+jH379lHz5s3Jw8NDbAObmJhI5cqVy3f8lnXoEQSBJk2apIhwFY7bWCohWbsbAJg4cSIuXryIyZMnw8nJCX379gUAREVFQV1dHeHh4QAAAwMD9O7dG0OGDIEgCHKvoYoMDAwQEBAATU1N1KhRQ9HhfJFEIoG1tTUyMzNx4sQJ1K5dGwBga2sLAHj79i369euHokWLYsuWLRg9ejSMjY2xZs0alChRQpGhs1+Uvb09oqKioK2tDUNDQ0WH80t69+4dnj17hsuXL+PmzZvYtm0bVq1aBWdnZ0ycOBF6enqYMGECJk2ahL1798LLy4uPFwrQuHFjaGtrY+7cuejTpw8WL16MUqVK4c2bN5BIJHLbGhkZoUuXLtDU1ESDBg0UFLFiCUT/a6nNlE5ISAjWrFmDadOmwdPTE6VLlwYAPH78GEuXLsXGjRvRoUMHjBs3Tu55lKeRsapTpbLcunULgwYNglQqxZw5c2BhYQEbGxsEBgZi+vTp4napqalIS0uDjo4OnyQY+8UdPnwY3t7eKF26NF6+fImZM2fC09MTdnZ2yM7ORrNmzVCiRAmsX79e0aH+kvKeg6KjozF37lw8fPgQffr0wbp16+Dt7Q1ra2tIpVJkZ2cjMzMTFSpUUIkKkcLCiaWSOnDgALp164Zt27ahWrVqICK8evUK9+7dQ7ly5SAIAmbNmoU5c+bg//7v/9C9e3dFh8yQm1wOHjwY7969w+XLl9G1a1fMnj0bAJCTkwMNDb5JwBiT9+DBg4/21pdKpWjXrh3s7e0REREBACp9J+pncPDgQSxevBjHjh3Dixcv0KJFCyQkJEAQBGhpaUEikWDTpk1wcHBQdKgKw2c5JfXq1SuYm5ujatWquHjxInbu3In169fjzZs3aNiwIebPn48ePXqgTJky6Nq1q6LDZf9Trlw58XaJgYEBWrZsKa5TtuGeGGPKwcLCAhYWFnLLsrKyMHHiRJw8eRKTJ0/mhPIHk9VUXrx4EU+fPoVUKoWvry+8vLwgCAJ0dHRw+fJlREREwMXFRXxeeno6ihYtqsDIFY9rLJXA+/fvoaurK7csNjYWbm5u8PHxQUxMDJo1a4YGDRpAW1sb/fr1w+7du+Wq2iUSCScuSuT27dsYOHAgiAhjx45FrVq1FB0SY0xFrF27FjExMYiKisLevXtRuXJlRYf0S9q6dSu6deuGUqVK4dGjR/D398fq1asBAIcOHcK8efPw5MkTTJs2TWxPqUrNtwoLJ5YKtmbNGiQmJiI0NBTa2togIkilUqirq+PkyZPYsmULqlevjoYNG6JkyZJIT09HvXr1MGPGDDRs2FDR4bPPuHXrFoYOHYrnz59j9uzZqF69uqJDYowpuZs3b6JPnz4wMjLC5MmT4ejoqOiQfimyxPDdu3do0qQJevbsidq1ayM+Ph5dunRBnTp1xIksjh49igkTJkAikeCff/7hger/hxNLBfrjjz/Qp08f7NmzBz4+PnIzXpw/fx4mJiawtLQEAGRnZyMjIwNt2rRBamoqjh8/zjWUKuDGjRsYO3YsZs2aJe5Lxhj7nJSUFO6tr0AHDhzAmjVroK6ujunTp8PExAQAcPLkSfj5+aF27drYtm0bBEHA8ePHYW1tjTJlyig4auXBiaWCrFmzBj169MCOHTvQtGlTuaRy27ZtCAoKwtatW1GvXj1kZ2dj4cKF2LJlC7KysnDy5Eloamqq/JBCv4qsrCxoaWkpOgzGGGNfISoqCoGBgTAwMMD169dRvHhxsSbz5MmTCAgIgKOjIw4ePPjL3/b+GM5KFGDlypXo2rUr6tevj6ZNmwLI7f0nCAJ27NiB1q1bY9KkSahXrx6A3GTTxcUFXl5eOHXqFDQ1NZGTk8NJpYrgpJIxxpSLVCr95OOWLVti3bp1SE9PR1hYGIB/5wevVasW1q9fj/v37yM5OfnHBaxCuMbyB4uMjESfPn3QvXt37NmzB61bt8bcuXMB5Lbt2LJlC169eoWgoKBPvgZ31GGMMca+z40bN7BmzRoEBQXB0tJSrvYxOzsb27dvR7du3dCzZ0/MmzdP7rkf63TLcnFi+QPNmTMHQ4cOxd9//40mTZpg6dKlCAsLQ4cOHcTkkjHGGGOFKzs7G7Vq1cL58+dhZ2eH3377DVWrVkVAQIC4TUZGBnbu3Ilu3bqhT58+4pjE7PN4HMsfqHLlyli/fj2aNGkCAGjXrh0EQcCYMWMAQEwuuUaSMcYYKzyampoICAhA+/bt4ezsjJMnT6J3797YtWsXatSogT59+kBHRwdt27YFALRv3x5aWlpys6ixj+MaSwXIO87VmzdvsHHjRowZM0au5pKTS8YYY6zwREdH47fffsOhQ4fg7u6Ox48f448//sCMGTNQsWJF9OjRAw0aNICdnR22b98OR0fHX3pGna/FiaUSkCWXYWFh6NixI1e3M8YYYz/AiBEj8PjxYyxbtgw6Ojpo164d4uLiUK1aNSQlJeH06dOYOXMmBg0axD3AvxLfClcCBgYG4m3x3r17w8rKCoMHD1Z0WIwxxthPrVq1avj999+hpaWFnj17Ijo6GocOHUKFChVw8+ZN7Nu3D56enpxUfgOusVQir1+/xtGjR9GsWTO+Dc4YY4z9APXq1cOJEydQqlQp7NmzR27ub/btOLFUUjk5OdDQ4AplxhhjrDDI+jvs2bMHQ4YMwfTp0+Hn58fzfX8nHmFbSXFSyRhjjBUeWfJYpUoVSKVSXLhwQW45+284sWSMMcbYL8vU1BTjx4/H7Nmzce7cOUWHo/I4sWSMMcbYL61Bgwbw8PCAubm5okNRedzGkjHGGGO/vIyMDOjo6Cg6DJXHiSVjjDHGGCsQfCucMcYYY4wVCE4sGWOMMcZYgeDEkjHGGGOMFQhOLBljjDHGWIHgxJIxxhhjjBUITiwZY4wxxliB4MSSMcaUlJWVFebMmSM+FgQBO3bs+OFxhIeHw9XV9ZPro6OjIQgCXr9+/dWvWb9+fQQHB39XXCtXrkSxYsW+6zUYYwWLE0vGGFMRjx8/RpMmTb5q2y8lg4wxVhg0FB0AY4z9zLKysqClpVUgr1WqVKkCeR3GGCssXGPJGGNfqX79+hgwYAAGDBgAQ0NDGBsbY+zYscg7gZmVlRUmTpyILl26wMDAAEFBQQCAEydOoE6dOtDV1YWFhQUGDRqE9PR08XkpKSlo3rw5dHV1YW1tjXXr1uV7/w9vhT98+BDt27dH8eLFUbRoUbi7u+Ps2bNYuXIlIiIiEBcXB0EQIAgCVq5cCQB4/fo1evbsiZIlS8LAwAANGzZEXFyc3PtMmzYNpqam0NfXR48ePZCRkfFNn9OLFy/Qvn17lC5dGkWKFEHFihWxYcOGfNvl5OR89rPMzMzE8OHDUbp0aRQtWhTVqlVDdHT0N8XCGPuxOLFkjLFvsGrVKmhoaODcuXOYO3cufv/9dyxbtkxum//7v/+Di4sLLl26hLFjxyIxMRE+Pj7w9/fH5cuXERUVhRMnTmDAgAHic7p164YHDx7gyJEj2LJlCxYtWoSUlJRPxpGWloZ69eohOTkZu3btQlxcHEaOHAmpVIq2bdti2LBhqFChAh4/fozHjx+jbdu2AICAgACkpKRg7969uHDhAtzc3ODp6YmXL18CADZt2oTw8HBMmTIF58+fh5mZGRYtWvRNn1FGRgaqVKmCv//+G1evXkVQUBA6d+6Mc+fOfdNnOWDAAJw+fRobN27E5cuXERAQAB8fH9y6deub4mGM/UDEGGPsq9SrV48cHR1JKpWKy0JCQsjR0VF8XLZsWfLz85N7Xo8ePSgoKEhu2fHjx0lNTY3ev39PN2/eJAB07tw5cX18fDwBoNmzZ4vLAND27duJiGjp0qWkr69PL168+Gis48ePJxcXl3zvaWBgQBkZGXLLbW1taenSpUREVKNGDerXr5/c+mrVquV7rbyOHDlCAOjVq1ef3MbX15eGDRsmPv7SZ3nv3j1SV1en5ORkudfx9PSk0NBQIiJasWIFGRoafvI9GWM/HrexZIyxb1C9enUIgiA+rlGjBmbNmgWJRAJ1dXUAgLu7u9xz4uLicPnyZbnb20QEqVSKpKQkJCQkQENDA1WqVBHXOzg4fLbHc2xsLCpXrozixYt/dexxcXFIS0tDiRIl5Ja/f/8eiYmJAID4+Hj06dNHbn2NGjVw5MiRr34fiUSCKVOmYNOmTUhOTkZWVhYyMzNRpEgRue0+91leuXIFEokE5cuXl3tOZmZmvvgZY8qDE0vGGCtgRYsWlXuclpaG3r17Y9CgQfm2tbS0REJCwje/h66u7jc/Jy0tDWZmZh9tp1iQw/bMnDkTc+fOxZw5c1CxYkUULVoUwcHByMrK+qZY1dXVceHCBTFhl9HT0yuwWBljBYsTS8YY+wZnz56Ve3zmzBmUK1cuX/KTl5ubG65fvw47O7uPrndwcEBOTg4uXLgADw8PAMDNmzc/Oy5kpUqVsGzZMrx8+fKjtZZaWlqQSCT54njy5Ak0NDRgZWX10dd1dHTE2bNn0aVLF7kyfouTJ0/it99+Q6dOnQAAUqkUCQkJcHJyktvuc59l5cqVIZFIkJKSgjp16nzT+zPGFIc77zDG2De4f/8+hg4dips3b2LDhg2YP38+Bg8e/NnnhISE4NSpUxgwYABiY2Nx69Yt7Ny5U+y8Y29vDx8fH/Tu3Rtnz57FhQsX0LNnz8/WSrZv3x6lSpWCn58fTp48iTt37mDr1q04ffo0gNze6UlJSYiNjcXz58+RmZkJLy8v1KhRA35+fti/fz/u3r2LU6dOYcyYMTh//jwAYPDgwfjzzz+xYsUKJCQkYPz48bh27do3fUblypXDgQMHcOrUKcTHx6N37954+vTpN32W5cuXR8eOHdGlSxds27YNSUlJOHfuHKZOnYq///77m+JhjP04nFgyxtg36NKlC96/f4+qVauif//+GDx4sDik0KdUqlQJR48eRUJCAurUqYPKlStj3LhxMDc3F7dZsWIFzM3NUa9ePbRq1QpBQUEwMTH55GtqaWlh//79MDExQdOmTVGxYkVMmzZNrDn19/eHj48PGjRogJIlS2LDhg0QBAF79uxB3bp1ERgYiPLly6Ndu3a4d+8eTE1NAQBt27bF2LFjMXLkSFSpUgX37t1D3759v+kzCgsLg5ubG7y9vVG/fn0xAf7Wz3LFihXo0qULhg0bBnt7e/j5+SEmJgaWlpbfFA9j7McRiPIMGsYYY+yT6tevD1dXV7lpFhljjP2LaywZY4wxxliB4MSSMcYYY4wVCL4VzhhjjDHGCgTXWDLGGGOMsQLBiSVjjDHGGCsQnFgyxhhjjLECwYklY4wxxhgrEJxYMsYYY4yxAsGJJWOMMcYYKxCcWDLGGGOMsQLBiSVjjDHGGCsQ/w8PVBS4AF4GjAAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"from torchmetrics import ConfusionMatrix\n",
"from mlxtend.plotting import plot_confusion_matrix\n",
"\n",
"# 2. Setup confusion matrix instance and compare predictions to targets\n",
"confmat = ConfusionMatrix(num_classes=len(class_names), task='multiclass')\n",
"confmat_tensor = confmat(preds=y_pred_tensor,\n",
" target=test_data.targets)\n",
"\n",
"# 3. Plot the confusion matrix\n",
"fig, ax = plot_confusion_matrix(\n",
" conf_mat=confmat_tensor.numpy(), # matplotlib likes working with NumPy \n",
" class_names=class_names, # turn the row and column labels into class names\n",
" figsize=(10, 7)\n",
");"
]
},
{
"cell_type": "markdown",
"id": "381c1c93-df30-451c-b65e-5d4c1680dc30",
"metadata": {
"id": "381c1c93-df30-451c-b65e-5d4c1680dc30"
},
"source": [
"Woah! Doesn't that look good?\n",
"\n",
"We can see our model does fairly well since most of the dark squares are down the diagonal from top left to bottom right (and ideal model will have only values in these squares and 0 everywhere else).\n",
"\n",
"The model gets most \"confused\" on classes that are similar, for example predicting \"Pullover\" for images that are actually labelled \"Shirt\".\n",
"\n",
"And the same for predicting \"Shirt\" for classes that are actually labelled \"T-shirt/top\".\n",
"\n",
"This kind of information is often more helpful than a single accuracy metric because it tells use *where* a model is getting things wrong.\n",
"\n",
"It also hints at *why* the model may be getting certain things wrong.\n",
"\n",
"It's understandable the model sometimes predicts \"Shirt\" for images labelled \"T-shirt/top\".\n",
"\n",
"We can use this kind of information to further inspect our models and data to see how it could be improved.\n",
"\n",
"> **Exercise:** Use the trained `model_2` to make predictions on the test FashionMNIST dataset. Then plot some predictions where the model was wrong alongside what the label of the image should've been. After visualing these predictions do you think it's more of a modelling error or a data error? As in, could the model do better or are the labels of the data too close to each other (e.g. a \"Shirt\" label is too close to \"T-shirt/top\")?"
]
},
{
"cell_type": "markdown",
"id": "25818e83-89de-496d-8b56-af4fc9f2acc5",
"metadata": {
"id": "25818e83-89de-496d-8b56-af4fc9f2acc5"
},
"source": [
"## 11. Save and load best performing model\n",
"\n",
"Let's finish this section off by saving and loading in our best performing model.\n",
"\n",
"Recall from [notebook 01](https://www.learnpytorch.io/01_pytorch_workflow/#5-saving-and-loading-a-pytorch-model) we can save and load a PyTorch model using a combination of:\n",
"* `torch.save` - a function to save a whole PyTorch model or a model's `state_dict()`. \n",
"* `torch.load` - a function to load in a saved PyTorch object.\n",
"* `torch.nn.Module.load_state_dict()` - a function to load a saved `state_dict()` into an existing model instance.\n",
"\n",
"You can see more of these three in the [PyTorch saving and loading models documentation](https://pytorch.org/tutorials/beginner/saving_loading_models.html).\n",
"\n",
"For now, let's save our `model_2`'s `state_dict()` then load it back in and evaluate it to make sure the save and load went correctly. "
]
},
{
"cell_type": "code",
"execution_count": 57,
"id": "d058e8fa-560f-4350-a154-49593ff403c9",
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/"
},
"id": "d058e8fa-560f-4350-a154-49593ff403c9",
"outputId": "0156a518-dae2-4b25-999a-c0a77ef7ef7c"
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Saving model to: models/03_pytorch_computer_vision_model_2.pth\n"
]
}
],
"source": [
"from pathlib import Path\n",
"\n",
"# Create models directory (if it doesn't already exist), see: https://docs.python.org/3/library/pathlib.html#pathlib.Path.mkdir\n",
"MODEL_PATH = Path(\"models\")\n",
"MODEL_PATH.mkdir(parents=True, # create parent directories if needed\n",
" exist_ok=True # if models directory already exists, don't error\n",
")\n",
"\n",
"# Create model save path\n",
"MODEL_NAME = \"03_pytorch_computer_vision_model_2.pth\"\n",
"MODEL_SAVE_PATH = MODEL_PATH / MODEL_NAME\n",
"\n",
"# Save the model state dict\n",
"print(f\"Saving model to: {MODEL_SAVE_PATH}\")\n",
"torch.save(obj=model_2.state_dict(), # only saving the state_dict() only saves the learned parameters\n",
" f=MODEL_SAVE_PATH)"
]
},
{
"cell_type": "markdown",
"id": "a1542284-8132-42ba-b00d-57e9b9037e4e",
"metadata": {
"id": "a1542284-8132-42ba-b00d-57e9b9037e4e"
},
"source": [
"Now we've got a saved model `state_dict()` we can load it back in using a combination of `load_state_dict()` and `torch.load()`.\n",
"\n",
"Since we're using `load_state_dict()`, we'll need to create a new instance of `FashionMNISTModelV2()` with the same input parameters as our saved model `state_dict()`."
]
},
{
"cell_type": "code",
"execution_count": 58,
"id": "634a8f7a-3013-4b45-b365-49b286d3c478",
"metadata": {
"id": "634a8f7a-3013-4b45-b365-49b286d3c478"
},
"outputs": [],
"source": [
"# Create a new instance of FashionMNISTModelV2 (the same class as our saved state_dict())\n",
"# Note: loading model will error if the shapes here aren't the same as the saved version\n",
"loaded_model_2 = FashionMNISTModelV2(input_shape=1, \n",
" hidden_units=10, # try changing this to 128 and seeing what happens \n",
" output_shape=10) \n",
"\n",
"# Load in the saved state_dict()\n",
"loaded_model_2.load_state_dict(torch.load(f=MODEL_SAVE_PATH))\n",
"\n",
"# Send model to GPU\n",
"loaded_model_2 = loaded_model_2.to(device)"
]
},
{
"cell_type": "markdown",
"id": "feeaebf4-6040-4fa5-852d-5eb8d2bbb94c",
"metadata": {
"id": "feeaebf4-6040-4fa5-852d-5eb8d2bbb94c"
},
"source": [
"And now we've got a loaded model we can evaluate it with `eval_model()` to make sure its parameters work similarly to `model_2` prior to saving. "
]
},
{
"cell_type": "code",
"execution_count": 59,
"id": "3e3bcd06-d99b-47bc-8828-9e3903285599",
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/"
},
"id": "3e3bcd06-d99b-47bc-8828-9e3903285599",
"outputId": "c0ee1d5f-9573-4e1a-8430-ee09fb4d72cd"
},
"outputs": [
{
"data": {
"text/plain": [
"{'model_name': 'FashionMNISTModelV2',\n",
" 'model_loss': 0.3285697102546692,\n",
" 'model_acc': 88.37859424920129}"
]
},
"execution_count": 59,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Evaluate loaded model\n",
"torch.manual_seed(42)\n",
"\n",
"loaded_model_2_results = eval_model(\n",
" model=loaded_model_2,\n",
" data_loader=test_dataloader,\n",
" loss_fn=loss_fn, \n",
" accuracy_fn=accuracy_fn\n",
")\n",
"\n",
"loaded_model_2_results"
]
},
{
"cell_type": "markdown",
"id": "c2b37855-c0da-4834-a2d4-a0faa8410b65",
"metadata": {
"id": "c2b37855-c0da-4834-a2d4-a0faa8410b65"
},
"source": [
"Do these results look the same as `model_2_results`?"
]
},
{
"cell_type": "code",
"execution_count": 60,
"id": "68544254-c99a-47ec-a32f-9816c21a993e",
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/"
},
"id": "68544254-c99a-47ec-a32f-9816c21a993e",
"outputId": "74b8d4ca-d35a-4f70-e8b9-ed54f034358e"
},
"outputs": [
{
"data": {
"text/plain": [
"{'model_name': 'FashionMNISTModelV2',\n",
" 'model_loss': 0.3285697102546692,\n",
" 'model_acc': 88.37859424920129}"
]
},
"execution_count": 60,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"model_2_results"
]
},
{
"cell_type": "markdown",
"id": "0ee07f93-4344-4c7a-8b1d-92a56034e7b2",
"metadata": {
"id": "0ee07f93-4344-4c7a-8b1d-92a56034e7b2"
},
"source": [
"We can find out if two tensors are close to each other using `torch.isclose()` and passing in a tolerance level of closeness via the parameters `atol` (absolute tolerance) and `rtol` (relative tolerance).\n",
"\n",
"If our model's results are close, the output of `torch.isclose()` should be true."
]
},
{
"cell_type": "code",
"execution_count": 61,
"id": "48dcf0ba-7e00-4406-8aaa-41918856361a",
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/"
},
"id": "48dcf0ba-7e00-4406-8aaa-41918856361a",
"outputId": "47324300-0d00-46de-d130-1283ad044ef8"
},
"outputs": [
{
"data": {
"text/plain": [
"tensor(True)"
]
},
"execution_count": 61,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Check to see if results are close to each other (if they are very far away, there may be an error)\n",
"torch.isclose(torch.tensor(model_2_results[\"model_loss\"]), \n",
" torch.tensor(loaded_model_2_results[\"model_loss\"]),\n",
" atol=1e-08, # absolute tolerance\n",
" rtol=0.0001) # relative tolerance"
]
},
{
"cell_type": "markdown",
"id": "c3969b7d-9955-4b6f-abf8-fe8eedf233a9",
"metadata": {
"id": "c3969b7d-9955-4b6f-abf8-fe8eedf233a9"
},
"source": [
"## Exercises\n",
"\n",
"All of the exercises are focused on practicing the code in the sections above.\n",
"\n",
"You should be able to complete them by referencing each section or by following the resource(s) linked.\n",
"\n",
"All exercises should be completed using [device-agnostic code](https://pytorch.org/docs/stable/notes/cuda.html#device-agnostic-code).\n",
"\n",
"**Resources:**\n",
"* [Exercise template notebook for 03](https://github.com/mrdbourke/pytorch-deep-learning/blob/main/extras/exercises/03_pytorch_computer_vision_exercises.ipynb)\n",
"* [Example solutions notebook for 03](https://github.com/mrdbourke/pytorch-deep-learning/blob/main/extras/solutions/03_pytorch_computer_vision_exercise_solutions.ipynb) (try the exercises *before* looking at this)\n",
"\n",
"1. What are 3 areas in industry where computer vision is currently being used?\n",
"2. Search \"what is overfitting in machine learning\" and write down a sentence about what you find. \n",
"3. Search \"ways to prevent overfitting in machine learning\", write down 3 of the things you find and a sentence about each. **Note:** there are lots of these, so don't worry too much about all of them, just pick 3 and start with those.\n",
"4. Spend 20-minutes reading and clicking through the [CNN Explainer website](https://poloclub.github.io/cnn-explainer/).\n",
" * Upload your own example image using the \"upload\" button and see what happens in each layer of a CNN as your image passes through it.\n",
"5. Load the [`torchvision.datasets.MNIST()`](https://pytorch.org/vision/stable/generated/torchvision.datasets.MNIST.html#torchvision.datasets.MNIST) train and test datasets.\n",
"6. Visualize at least 5 different samples of the MNIST training dataset.\n",
"7. Turn the MNIST train and test datasets into dataloaders using `torch.utils.data.DataLoader`, set the `batch_size=32`.\n",
"8. Recreate `model_2` used in this notebook (the same model from the [CNN Explainer website](https://poloclub.github.io/cnn-explainer/), also known as TinyVGG) capable of fitting on the MNIST dataset.\n",
"9. Train the model you built in exercise 8. on CPU and GPU and see how long it takes on each.\n",
"10. Make predictions using your trained model and visualize at least 5 of them comparing the prediciton to the target label.\n",
"11. Plot a confusion matrix comparing your model's predictions to the truth labels.\n",
"12. Create a random tensor of shape `[1, 3, 64, 64]` and pass it through a `nn.Conv2d()` layer with various hyperparameter settings (these can be any settings you choose), what do you notice if the `kernel_size` parameter goes up and down?\n",
"13. Use a model similar to the trained `model_2` from this notebook to make predictions on the test [`torchvision.datasets.FashionMNIST`](https://pytorch.org/vision/main/generated/torchvision.datasets.FashionMNIST.html) dataset. \n",
" * Then plot some predictions where the model was wrong alongside what the label of the image should've been. \n",
" * After visualing these predictions do you think it's more of a modelling error or a data error? \n",
" * As in, could the model do better or are the labels of the data too close to each other (e.g. a \"Shirt\" label is too close to \"T-shirt/top\")?\n",
"\n",
"## Extra-curriculum\n",
"* **Watch:** [MIT's Introduction to Deep Computer Vision](https://www.youtube.com/watch?v=iaSUYvmCekI&list=PLtBw6njQRU-rwp5__7C0oIVt26ZgjG9NI&index=3) lecture. This will give you a great intuition behind convolutional neural networks.\n",
"* Spend 10-minutes clicking thorugh the different options of the [PyTorch vision library](https://pytorch.org/vision/stable/index.html), what different modules are available?\n",
"* Lookup \"most common convolutional neural networks\", what architectures do you find? Are any of them contained within the [`torchvision.models`](https://pytorch.org/vision/stable/models.html) library? What do you think you could do with these?\n",
"* For a large number of pretrained PyTorch computer vision models as well as many different extensions to PyTorch's computer vision functionalities check out the [PyTorch Image Models library `timm`](https://github.com/rwightman/pytorch-image-models/) (Torch Image Models) by Ross Wightman."
]
}
],
"metadata": {
"accelerator": "GPU",
"colab": {
"gpuType": "A100",
"machine_shape": "hm",
"provenance": []
},
"gpuClass": "standard",
"kernelspec": {
"display_name": "Python 3 (ipykernel)",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.8.13"
},
"vscode": {
"interpreter": {
"hash": "3fbe1355223f7b2ffc113ba3ade6a2b520cadace5d5ec3e828c83ce02eb221bf"
}
}
},
"nbformat": 4,
"nbformat_minor": 5
}